卫星信道中高阶APSK调制的非线性失真补偿算法

(解放军理工大学 通信工程学院 卫星通信教研室，南京210007)

1 引 言

随着卫星宽带业务需求的增长，频谱带宽资源趋于紧张，因此频带利用率和功率有效性更高的幅度相位联合调制的高阶APSK调制技术得到了广泛应用。但由于信号幅度的变化，APSK对卫星信道的非线性失真极其敏感，容易产生邻道干扰和码间串扰。为保证通信性能，必须对信道的非线性失真进行补偿。

目前常用的补偿措施主要分两类：一是在发送端进行预失真处理，二是在接收端进行非线性均衡[1]。非线性均衡[2]能够有效降低码间串扰，但不能保证功率资源和频率资源的有效利用。根据是修改发送数据的星座还是修改发送信号的波形，预失真技术分为数据预失真和信号预失真两种[3]。信号预失真采用数学模型描述非线性信道的逆特性，由于非线性的模型很多，所以信号预失真的实现方法多，结构灵活，但普遍存在计算量大的问题。数据预失真[4-6]针对信号的星座进行处理，不需要拟合信道模型，主要分为无记忆数据预失真和有记忆数据预失真[7]两种。本文重点研究基于数据预失真的补偿算法。

随着通信速率的增加，信号带宽不断增加，卫星信道不仅具有非线性特性，其记忆效应也越来越明显。卫星信道的这种有记忆非线性特性使得传统补偿技术的性能严重下降。目前，有关数据预失真算法的研究只是针对无记忆非线性信道，没有考虑信道的记忆特性。文献[3]指出在无记忆非线性信道中采用无记忆数据预失真联合非线性均衡实现非线性补偿，也没有考虑信道的记忆效应。

本文首先验证了有记忆的数据预失真算法可以有效地抵抗记忆效应的影响。但是，由于有记忆数据预失真查询表的大小为Mk(其中M为调制的阶数，k为记忆长度)，在记忆长度一定时，高阶调制所需的查询表以及自适应迭代的计算量将很大，这就制约了有记忆数据预失真算法在实际中的应用。因此，本文首先提出一种基于APSK调制的简化无记忆数据预失真算法，然后联合非线性均衡技术，实现对有记忆非线性卫星信道的有效补偿。

2 系统模型

图1 系统仿真模型Fig.1 System simulation model

本文采用的有记忆非线性卫星信道模型如图1所示，发送端和接收端均采用平方根升余弦滤波器。卫星高功放采用线性FIR滤波器串联无记忆非线性模型，无记忆非线性模型采用Saleh提出的TWTA模型的变形模型[5]，其输入输出关系为

Sout(t)=Sin(t)G(r)ejφ(r)

(1)

(2)

(3)

3 自适应补偿算法

当信号带宽较宽时，卫星信道呈现出有记忆的非线性特性。理想星座经过信道后，如果不采用任何补偿措施，接收到的星座会发生严重扭曲，并且信号星座点发散很严重。自适应数据预失真的基本原理是通过修改发送端信号映射星座图，使接收端(接收滤波器输出端)的信号星座尽可能靠近理想星座。根据预失真值与输入数据的前后码元是否有关，数据预失真分为无记忆数据预失真和有记忆数据预失真两种。前者方法简单，易于实现；后者可以有效降低码间串扰，提高补偿性能。

自适应数据预失真是通过查询表的方法实现的，即把输入数据作为查询表的地址，预失真值作为查询的内容[3]。设当前输入数据为an，则一个记忆长度为K=2L+1的预失真器的输出数据bn是输入向量(an-L,…,an-1,an+1,…,an+L)的函数。预失真的最优化采用最小均方误差准则[6]，均方误差定义为

D=E{|E(yn|bn)-an|2}

(4)

式中，yn是预失真数据bn的输出数据。

预失真技术的实现步骤是：

(1)计算匹配滤波器输出信号各星座点的中心：

Cn=E(yn|bn)

(5)

(2)计算输出信号星座点中心和目标星座点的幅度和相位误差：

(6)

(7)

(3)通过迭代不断更新当前数据的预失真值，迭代公式为

(8)

(9)

式中，βr、βθ为幅度和相位的步长因子，rn(k)、θn(k)分别表示预失真数据yn的幅度和相位。

根据APSK调制方式的特点和非线性转移特性，本文提出一种简化的无记忆数据预失真算法。即当记忆长度为1，也即无记忆时，由于非线性模型的幅度和相位变化仅与当前输入信号的幅度有关，因此APSK信号的同圈星座点具有相同的幅度相位转移特性，可以做相同的预失真处理，即每次迭代只需计算同圈信号的一个星座点，根据该点的误差对整圈星座点做整体的调整。由于APSK信号的星座圈数较少，所以对于APSK调制技术，简化的无记忆数据预失真可以大幅度减少计算量和存储量。例如16APSK每次迭代只需计算2个信号点，32APSK每次迭代只需计算3个信号点。

正如上文所述，有记忆数据预失真可以有效降低码间串扰，但其缺点是：当信号的进制数较高或记忆长度较大时，查询表的大小会急剧增加，并且有记忆预失真不能采用上述无记忆预失真的简化计算方法，所以其存储量和计算量都很大，可实现性不高。针对此问题，本文提出采用发送端的无记忆数据预失真联合接收端的非线性均衡实现对有记忆非线性卫星信道的有效补偿。

本文采用比较适合卫星链路的三阶非线性均衡器，即记忆长度为3个符号[3]。均衡器的输入输出关系为

(10)

式中，xn、yn是均衡器在n时刻的输入输出采样值，hm1、hm1,m2,m3为非线性均衡器的系数。系数的最优化采用LMS算法，hopt=min[E{|yn-an|2}]，迭代公式为h(n+1)=h(n)+μy(n)e*(n)，其中an为输出序列yn的期望值，误差e(n)=yn-an。

4 仿真结果

仿真时采用16APSK调试方式，发送和接收滤波器为平方根升余弦滤波器，滚降因子均取0.5，每个符号8个采样点。卫星高功放采用FIR滤波器串联无记忆的Saleh模型，其中FIR滤波器的系数取[0.769 2 0.153 8 0.076 9]，其输入输出关系如图2所示。

本文仿真采用两种结构，即有记忆数据预失真和联合结构(简化的无记忆数据预失真联合非线性均衡)。有记忆数据预失真的记忆长度为3个符号，步长因子取0.5。联合结构的自适应过程分为两个阶段，即无记忆数据预失真和非线性均衡，无记忆数据预失真采用第3节中的简化计算方法，步长因子取0.5；非线性均衡中滤波器系数初始化为0，步长因子取0.001。图3为不采用预失真处理的输出信号星座图。由于非线性和记忆效应，信号点发散且扭曲严重。图4、图5分别为采用无记忆和有记忆数据预失真的输出信号星座图，可见无记忆数据预失真能够矫正星座的扭曲现象，但信号点仍然发散严重，而采用有记忆数据预失真能够有效地消除码间串扰，使信号点相对集中。图6为采用无记忆数据预失真联合非线性均衡得到的信号星座图，与图5相比，信号点更加集中。

图2 记忆非线性高功放的AM/AM和AM/PM特性Fig.2 AM/AM and AM/PM characteristics of the nonlinear HPA with memory

图3 无预失真输出信号星座图Fig.3 Output signal constellation without predistortion

图4 无记忆数据预失真输出信号星座图Fig.4 Output signal constellation with memoryless data predistortion

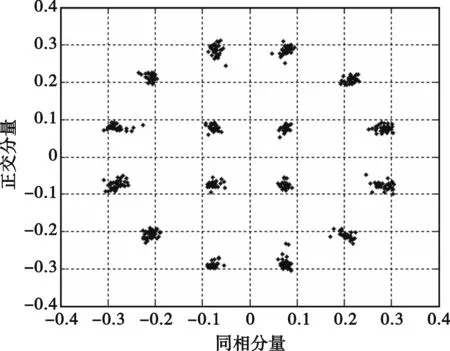
图5 有记忆数据预失真输出信号星座图Fig.5 Output signal constellation with memory data predistortion

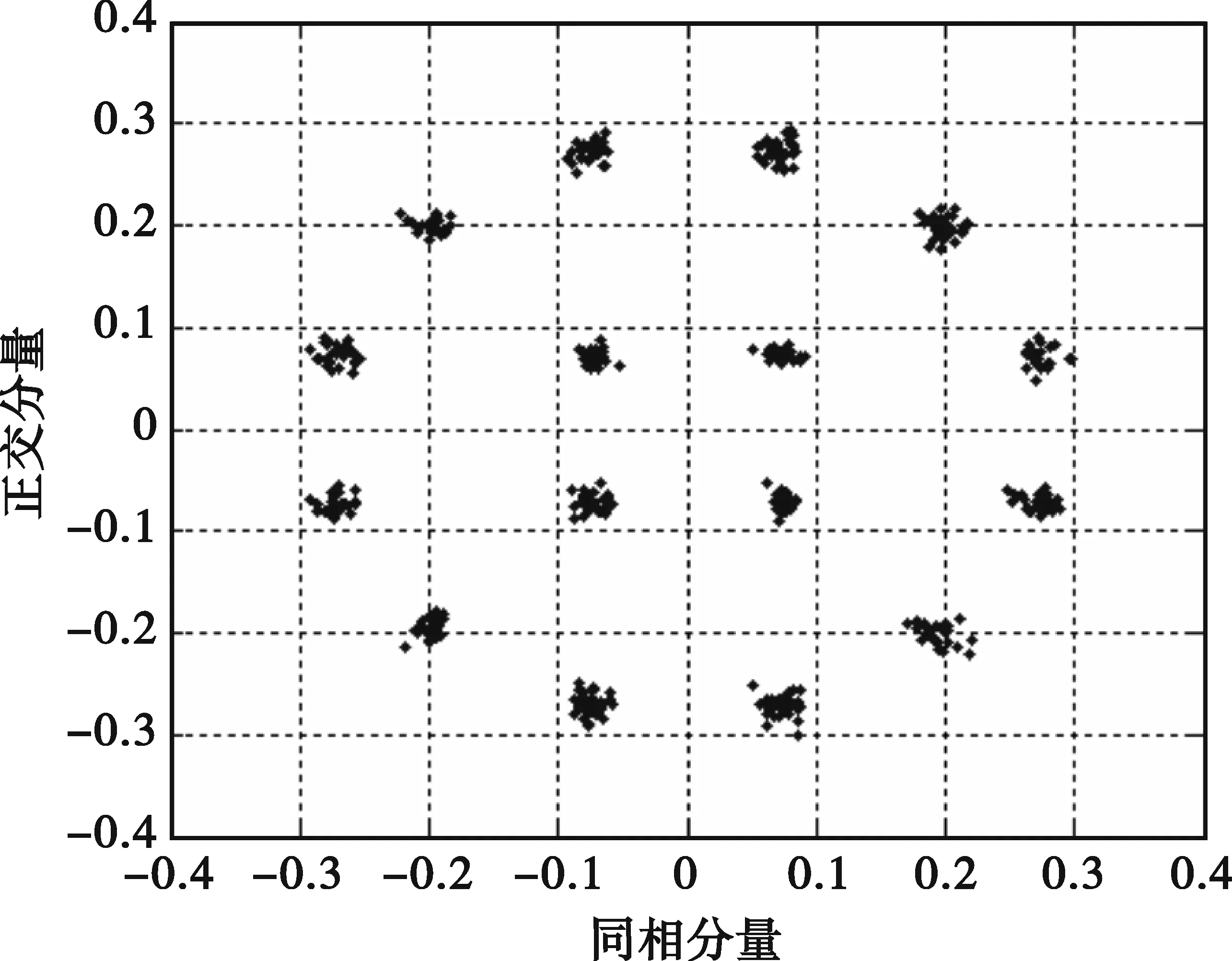
图6 联合矫正后的输出信号星座图Fig.6 Output signal constellation with combined compensation scheme

为了能够衡量有记忆数据预失真方法和联合方法在有记忆非线性系统中的性能以及确定不同方式下的最佳工作点，定义参数TD=OBO+ΔSNR，其中OBO为高功放的输出补偿，ΔSNR为误码率为10-3时非线性信道和线性信道所需的信噪比之差。仿真结果如图7所示，可以看出，两种方法的性能非常相近，有记忆数据预失真的最佳工作点在1.8 dB左右，联合模型的最佳工作点在1.6 dB左右。

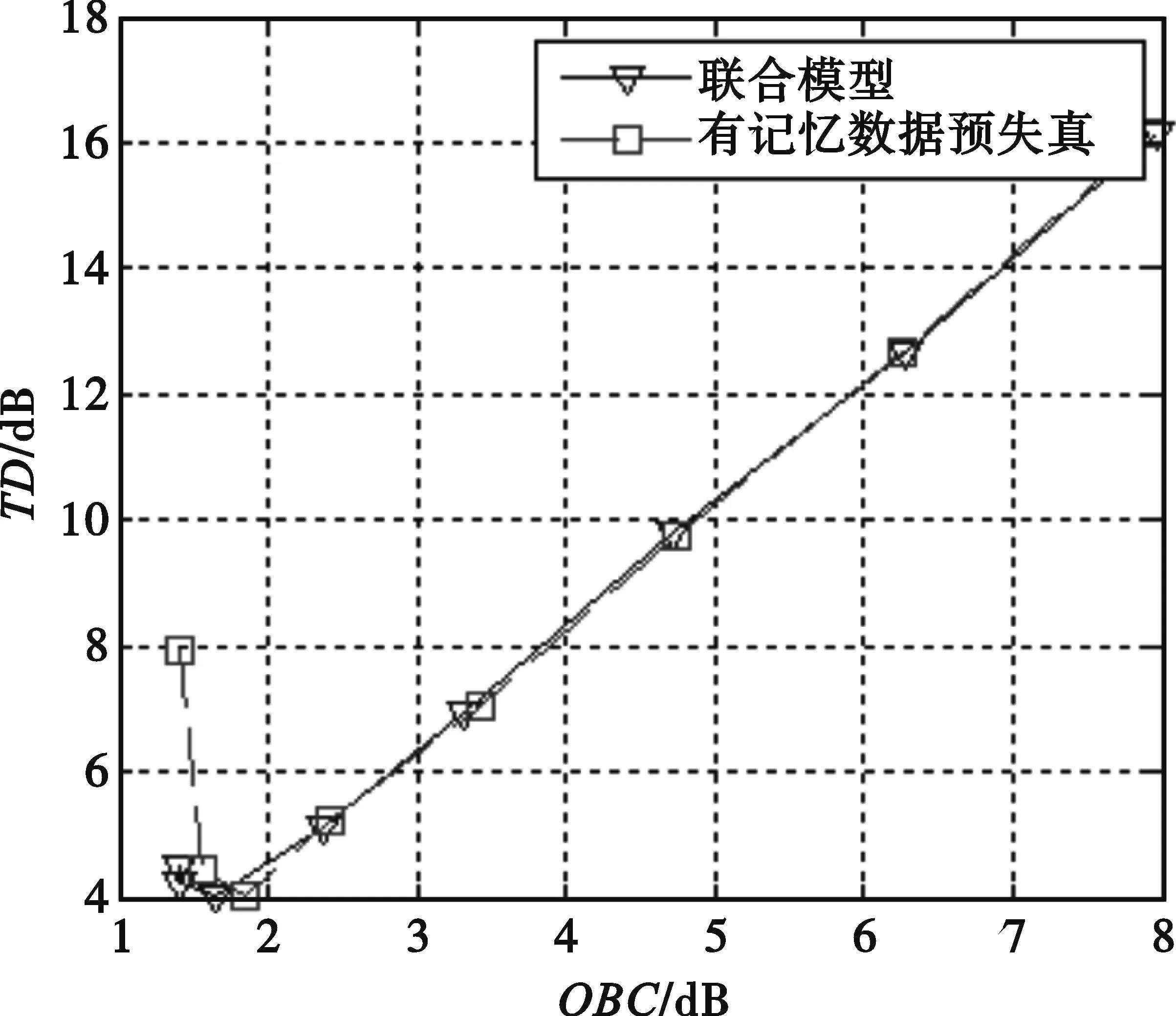
图7 16APSK在两种补偿措施下的性能曲线Fig.7 Performance of 16APSK with the two different compensation schemes

5 结 论

本文提出采用发送端简化的无记忆数据预失真算法联合接收端的非线性均衡技术实现对有记忆非线性卫星信道的自适应补偿，该联合算法的突出优点是在达到有记忆数据预失真算法性能指标的基础上，其存储量和计算复杂度随调制阶数的增加变化很小，并且最佳工作点比有记忆数据预失真技术提高0.2 dB。但由于该算法中采用了非线性均衡，当记忆长度增加时，非线性均衡所引入的计算复杂度也会随之加大，所以在进一步的工作中，研究实现简单且性能好的均衡技术是非常必要的。

参考文献：

[1] 李爱红.基于离散小波变换的Volterra自适应预失真方法[J]. 信号处理, 2009, 25(1):40-43.

LI Ai-hong. A Method of Adaptive Volterra Predistortion Based on the Discrete Wavelet Transform[J]. Signal Processing, 2009, 25(1):40-43. (in Chinese)

[2] Karam G, Sari H. Analysis of predistortion, equalization, and ISI cancellation techniques in digital radio systems with nonlinear transmit amplifiers[J]. IEEE Transactions on Communications, 1989, 37(12): 1245-1253.

[3] Luca Giugno, Marco Luise. Adaptive Pre- and Post-Compensation of Nonlinear Distortions for High-Level Data Modulations[J]. IEEE Transaction on Wireless Communications,2004,3(5):1490-1495.

[4] 赵金旺.16QAM调制在非线性卫星信道中的性能研究[J]. 军事通信技术, 2006, 27(1):12-16.

ZHAO Jin-wang. Performance Research of 16 QAM Modulations over Nonlinear Satellite Channnels[J].Military Communications Technology, 2006, 27(1):12-16. (in Chinese)

[5] ZHOU Yu-gang, McLane. Performance of Predistorted APK Modulation for One-and Two-Link Nonlinear Power Amplifier Satellite Communication Channels[J]. IEEE Transactions on Vehicular Technology, 2005, 54(2):630-638.

[6] Riccardo, Albert. Performance Analysis of Turbo-Coded APSK Modulations over Nonlinear Satellite Channels[J]. IEEE Transaction on Wireless Communications, 2006, 5(9):2396-2407.

[7] Karam G, Sari H. A Data Predistortion Technique with Memory for QAM Radio Systems[J]. IEEE Transactions on Communications, 1991,39(2):336-343.

[8] Saleh A A M. Frequency-independent and Frequency-dependent Nonlinear Models of TWT Amplifiers[J]. IEEE Transactions on Communications, 1981,29(11):1715-1720.