一种新的定时和频偏联合估计算法

韩艳春1,，钟雪锋，鲁 军

(1.重庆大学 通信工程学院, 重庆 400044；2.重庆通信学院, 重庆 400035)

1 引 言

正交频分复用(OFDM)技术是一种多载波传输技术，因为它具有频带利用率高、抗干扰和抗衰落能力强等优点，因此受到人们的广泛关注。但是，OFDM的一个致命缺陷是对同步误差特别敏感，同步性能的好坏直接影响到接收的性能；而且同步性能不好，OFDM系统的整体性能就会严重下降，因此快速准确地进行定时同步和载波频率同步对OFDM系统的实现是非常重要的。

在大多数定时同步方法中，最普遍采用的方法是寻找两个重复的采样序列之间的最大相关值。 一种是基于循环前缀的定时同步算法[1]，它主要利用循环前缀与OFDM符号的最后一部分完全相同这一特性来实现的，但是由于循环前缀会受到符号间干扰(ISI)的影响，因此这种方法的精度不高。文献[2]采用了保护间隔中没有遭受符号间干扰(ISI)的部分进行定时估计。另一种是基于训练符号的定时估计算法，Schmidl和Cox[3]提出了一种基于训练符号的定时算法，该算法中使用了由前后两个相同部分组成一个训练符号进行定时估计，但是，其定时测度为一个平台，这会引起一个较大的定时估计方差，H.Minn[4]对Schmidl和Cox的算法进行了改进，其定时测度为尖峰，但是,在子载波数目较小的系统中，在其它时刻也会产生多个尖峰，而且有时错误时刻的峰值会超过正确时刻的峰值。在OFDM系统中，频率同步往往也采用训练符号来完成。在文献[5]中，P.Moose提出了一种频域中的最大似然(ML)估计算法，它利用了两个训练符号在频域进行频偏估计，其估计精度很高，但复杂度高，且估计范围为子载波频率间隔的一半。本文提出了一种新的基于训练符号的OFDM系统符号定时算法,该算法仅利用一个训练符号便能实现定时估计和频偏估计，算法中给出的定时测度消除了Schmidl&Cox算法中出现的定时测度平台和H.Minn算法中多峰值现象，而且，频偏估计的复杂度大大减小。仿真结果表明，即使在频率选择性衰落信道中，本文提出的算法也能快速地实现定时和频率捕获。

2 OFDM系统描述

在OFDM系统的复基带等效模型中，发送端的OFDM复基带已调信号可表示为

(1)

式中，N为系统子载波的数目，X(k)为第k个子载波上调制的复数据。

该信号经过信道传输后，接收端的符号定时偏移通常表示为接收信号的时延，载波的频率偏移通常表示为时域上的相位失真，因此具有符号定时偏差和载波频偏的OFDM系统的接收信号可表示为

(2)

r(n)=y(n-τ)ej(2πεn/N+φ)+w(n)

(3)

式中，h(m)为信道的脉冲响应，L表示信道的多径数，τ为定时偏差，ε为载波频偏，φ为初始相位。

同步的主要任务是估计符号定时偏差τ和载波频偏ε，并通过补偿来消除或减弱同步误差对系统性能的影响。

3 算法描述

本文根据IEEE 802.11a标准中长训练序列具有共轭对称的特点，采用了共轭对称的训练序列进行符号定时同步估计，其定时测度为一尖脉冲。其帧结构如图1所示，A与B对称，B*为B的共轭。

图1 基于共轭对称训练序列的符号定时同步算法的帧结构图Fig.1 Frame structure of the timing algorithm based on conjugate symmetry sequences

因此有：

(4)

不考虑噪声的影响，接收到的信号可以表示为

y(k)=s(k)ej2πεk/N

(5)

所以有：

(6)

(7)

(8)

如果在一个窗口对多个输出序列的乘积累加，则会出现一个相关峰，因此定义：

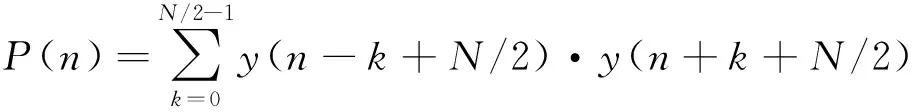
(9)

接收到信号的能量为

(10)

对P(n)进行归一化，得到基于共轭对称训练序列的符号定时算法的定时测度表达式为

(11)

定时测度最大值对应的时刻就是参考符号的第一个样点时刻，即：

(12)

具有共轭对称训练序列的符号定时同步算法的相关运算示意图如图2所示。由图可以看出，P(n+1)和P(n)参与相关运算的数据序列是完全不同的，这样P(n+1)和P(n)是随机独立的，加上序列的共轭对称性，使得P(n)只有在准确定时点才会出现明显的单峰值，而其它时刻对应的测度值较小。因此， 应用训练符号结构，在一定的时间窗内搜索这个最大峰值就可以准确得出定时误差。此外，由于测度计算中采用了自相关处理，载波频率偏差可以视为一个恒定的相移量，所以本文算法对载波频率偏差具有鲁棒性。

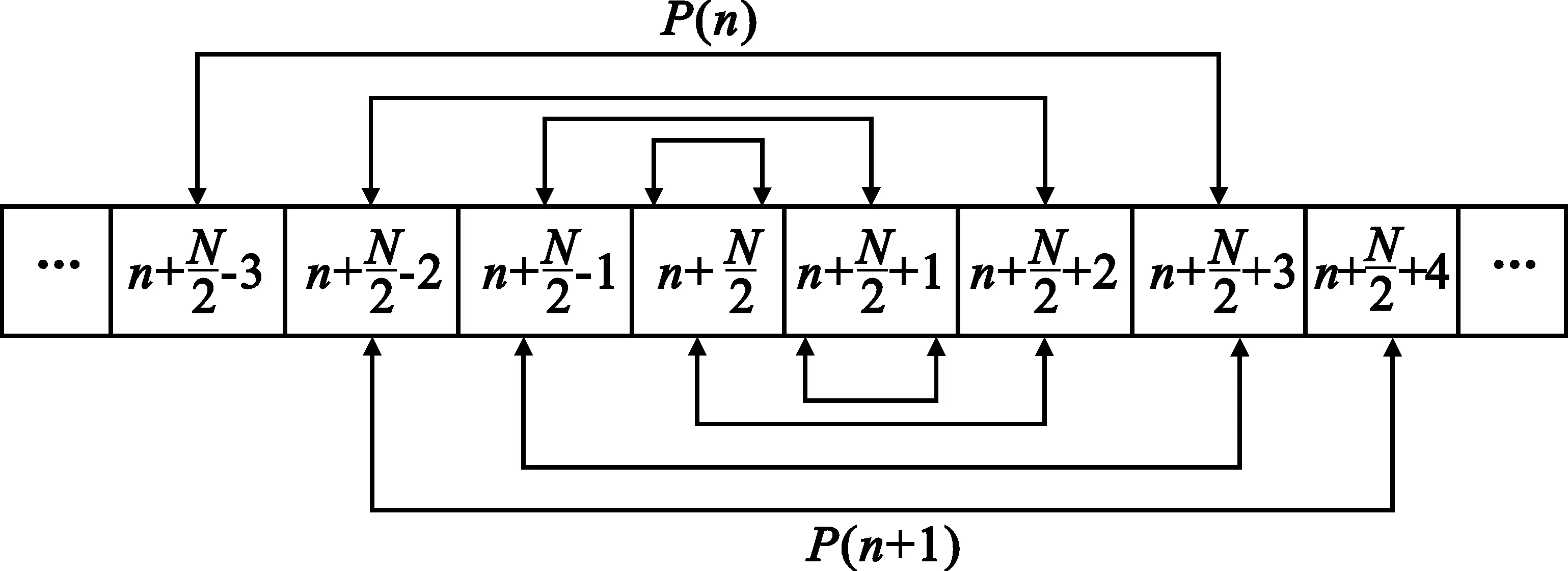
图2 训练符号的相关示意图Fig.2 Correlation of training symbol

利用共轭对称训练符号对载波频偏进行估计，这种算法只利用一个训练符号就可以同时完成定时同步和载波频率偏差的估计，这样既可以降低系统的开销又降低了实现的复杂度。

令P为

[s(N/2+k)ej2πε(N/2+k)/N+w(N/2+k)]=

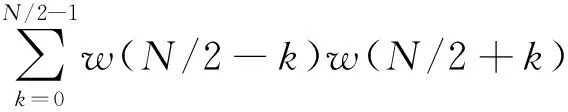
(13)

式(13)右边的后三项都为噪声项，相对相关项是很小的，因此不考虑噪声的影响，有：

(14)

则载波频率偏差为

(15)

由于P的相位超出π后存在相位模糊，即：

(16)

因此估计范围为

(17)

然后用估计值对频率偏差进行补偿，即：

(18)

(19)

通过以上分析可以看出，提出的算法只用了一个训练序列就完成了与P.Moose算法几乎一样的估计范围和方差。

4 仿真分析

下面对以上算法进行仿真分析，仿真参数的设置如下：调制方式为QPSK，FFT点数为64，有用子载波数48个，导频4个，循环前缀16个。用估计误差的均值和估计误差的标准方差作为描述系统性能的指标，仿真环境为在加性白高斯噪声AWGN信道和多径信道。

图3 不同信噪比下算法的定时测度Fig.3 Timing metric in different SNRs

不同信噪比下，其定时测度如图3所示(为了比较方便，假设正确定时时刻为0)。从图中可以看出，其定时测度为一个尖的脉冲，即使在信噪比很低的情况下，其仍然为一尖脉冲，且其峰值也远远高于其它分量，这样可以很快地检测出最高峰，而且定时的精度也会提高。

图4给出了系统的载波频率偏差为232 kHz时的定时测度，可以看出频偏对它的影响是非常小的，即使存在很大的载波频率偏差，定时测度也不会有很大的变化，因此文中算法仍然能够精确地完成定时估计。

图4 存在频偏时算法的定时测度Fig.4 Timing metric in present of frequency offset

在加性高斯白信道中，在不同的平均信道信噪比情况下，对文中定时估计算法和文献[4]的H.Minn算法仿真得到的定时估计同步误差的均值和估计误差的标准方差分别如图5和图6所示。多径信道下，对两种定时估计算法仿真得到的定时估计同步误差的均值和估计误差的标准方差分别如图7和图8所示。

图5 AWGN中两种算法的均值比较Fig.5 Mean of two estimators in AWGN channel

图6 AWGN中两种算法的标准方差比较Fig.6 Standard variance of two estimators in AWGN channel

图7 多径信道中两种算法的均值比较Fig.7 Mean of two estimators in mulitipath channel

图8 多径信道中两种算法的标准方差比较Fig.8 Standard variance of two estimators in multipath channel

从图5可以看出， H.Minn算法即使在信噪比较高时，定时估计值也会偏离正确定时时刻，而文中符号定时算法在信噪比达到6 dB时，均值为0，就可以实现准确定时；而且由图6也可以看出，文中的符号定时算法的标准方差也小于H.Minn算法的标准方差，当信噪比达到6 dB时，标准方差为0。由图7和图8可以看出，在多径信道中，文中的符号定时算法当信噪比达到10 dB时，均值为0；且其标准方差也趋近于0；而H.Minn算法在多径信道中，无论信噪比多大，其方差都不为零，因此在多径条件下，文中的符号定时算法的性能仍然优于H.Minn算法。

基于共轭对称训练序列的频率偏差估计算法的均值和方差的仿真结果分别如图9和图10所示。

图9 载波频率偏差估计的均值Fig.9 Mean of carrier frequency offset estimation

图10 载波频率偏差估计的方差Fig.10 Variance of carrier frequency offset estimation

基于共轭对称训练序列的频率偏差估计算法是在时域内完成频率偏差的估计，避免了两次FFT操作，复杂度要低得多；与P.H.Moose算法相比，该频率偏差估计算法使用的训练序列长度为P.H.Moose算法的一半，且使用的复乘法器和复加法器要远远小于P.H.Moose算法，但它完成的性能与P.H.Moose算法相同。

5 结 论

本文提出了一个新的OFDM系统定时和频偏联合估计算法。该算法中仅使用了一个训练符号，因此其额外开销量小，相对地降低了系统实现难度。定时测度中，准确定时时刻会出现的一个明显的尖脉冲，能快速准确地实现定时，而且即使存在频偏也能精确估计出符号定时误差，通过仿真可以看出即使在多径信道下，也能较好地实现定时估计，定时估计完成后，用于定时的训练符号也被用来进行频偏估计，其估计精度与P.Moose相同，但复杂度要远远低于P.Moose算法。

参考文献：

[1] Beek J J, Sandell M, Borjesson P O. ML estimation of time and frequency offset in OFDM systems[J]. IEEE Transactions on Signal Processing,1997,45(7):1800-1805.

[2] Speth M, Classen F, Meyr H. Frame synchronization of OFDM systems for frequency selective fading channels[C]// Proceedings of IEEE 47th Vehicular Technology Conference. Phoenix, AZ :IEEE,1997: 1807-1811.

[3] Schmidl T M, Cox D C. Robust frequency and timing synchronization for OFDM[J]. IEEE Transactions on Communications，1997,45(12):1613-1621.

[4] Minn H,Bhargava V K.On timing offset estimation for OFDM systems [J]. IEEE Communications Letters,2000,4(7):242-244.

[5] Moose P H. A technique for orthogonal frequency division multiplexing frequency offset correcting[J]. IEEE Transactions on Communications,1994,42(10):2908-2914.