部分涂敷目标的RCS仿真计算
2010-09-27童创明
吕 丹,童创明
(1.空军工程大学 导弹学院,陕西 三原 713800;2.毫米波国家重点实验室,江苏 南京 210096)
1 引 言
雷达散射截面(RCS)定量描述了目标的散射强弱程度,如果能减缩目标的RCS,则能迫使敌方电子探测系统和武器平台降低其战斗效能,从而提高我方目标的突防和生存能力。通常,有4种方案可以用于减缩目标RCS,分别是外形隐身技术、雷达吸波材料隐身技术、无源对消技术和有源对消技术[1]。外形上的修改使得目标的RCS在一定的角度上减小,但在另一些角度上又会增加,而且还要考虑外形带来的气动特性和机动特性问题;无源对消技术随着频率和观察角的微小变化难以控制RCS的增大或减缩效果;有源对消技术又因为所要求的各种硬件和软件技术的复杂度难以实施。所以,在目标表面涂敷雷达吸波材料成为当前最流行的减缩目标RCS的途径。如果只要求目标在一定的角度范围内有较小的RCS,那么就没有必要将目标全身涂敷吸波材料,只要在需要的部位上涂敷就可达到性能要求。
参数曲面建模是现在最为流行的模拟目标外形的方法,具有以下伏点:可以更加方便地定义、修改模型,获取目标的几何信息;不会引入面元噪声,提高了计算精度;降低了划分曲面的数量,提高了计算速度等[2-4]。在非均匀有理B样条(NURBS)参数建模的基础上运用物理光学法计算了电大尺寸目标部分涂敷情况下的后向RCS。计算结果证明,部分涂敷吸波材料在特定的角度范围内起到了减缩目标的RCS作用。
2 理论方法
2.1 物理光学场积分方程
当平面波入射导体目标时,边界条件满足
利用远场近似,得到散射电场的表达式为
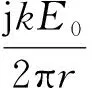
(1)

对于表面涂敷吸波材料的导体目标,表面散射场可以表示为

(2)
式中,Z0为本征阻抗,E和H分别为表面的总电场和总磁场,有E=Ei+Es,H=Hi+Hs。

图1 介质表面散射示意图 Fig. 1 Scattering field at the surface

(3)
(4)
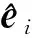
(5)
(6)
经计算[5]:

(7)

(8)
2.2 反射系数


图2 多层有耗介质示意图Fig. 2 Geometry of multilayered panel
介质的散射需要考虑入射波的极化方式,相应的总反射系数也分为平行极化反射系数R‖和垂直极化反射系数R⊥。R‖和R⊥由下列公式递推得到[6-7]:
(9)
(10)

(11)
(12)
其中c(n)=k(n)cosα(n),
(13)
(14)
当n=N时,有:
(15)

将式(9)、式(10)及式(7)、式(8)代入式(2)便得到涂敷目标的散射电场。与式(1)比较发现,只要将反射系数公式中的涂层厚度设置为0就可计算导体目标的散射场。
2.3 非均匀有理B样条参数曲面
一张k×l次的NURBS曲面方程表示为[2-4]
(16)
式中,控制顶点di,j(i=0,1,2,…,m;j=0,1,2,…,n)呈拓扑矩形阵列,形成一个控制网格,ωi,j是与顶点di,j相联系的权因子,Ni,k(u)(i=0,1,2,…,m)和Nj,l(v)(j=0,1,2,…,n)分别为u向k次和v向l次的规范B样条基。
在NURBS模型上,
(17)
将式(16)与式(17)代入式(3),并通过RCS的定义得到基于NURBS曲面的RCS表达式。
3 计算结果
计算部分涂敷目标的RCS时采用统一的积分式计算散射场,只是有涂敷部分的涂层厚度不为0,导体部分的涂层厚度设置为0。然后叠加两部分的散射场得到总的散射场,近而计算目标的后向RCS。
圆柱直径为3λ,长为4λ。RAM的相对介电常数和相对磁导率分别为εr=4-j1.5和μr=2-j1,涂层厚度为0.04λ,入射波频率为10 GHz,水平极化。目标上灰色表示涂敷吸波材料的部分,考虑只涂敷圆柱顶端圆面,如图3所示。圆柱未涂敷、全部涂敷以及部分涂敷情况下的RCS如图4所示。另外,还考虑将圆柱的一半涂敷吸波材料,如图5所示,同样将3种情况下的RCS进行了比较,如图6所示。
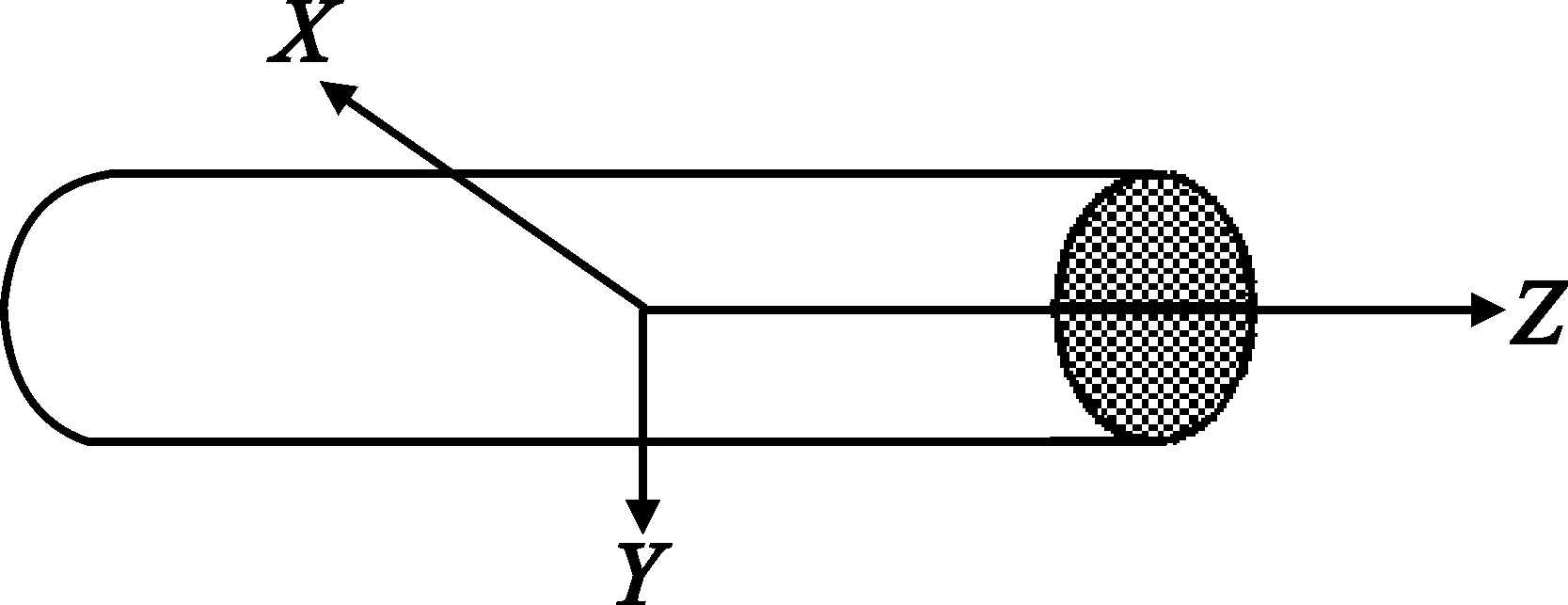
图3 圆面顶端部分涂敷示意图Fig. 3 Geometry of partially coated colum

图4 未涂敷与涂敷圆柱的RCS(顶端)Fig. 4 RCS of column coated without and with RAM(top)
从图4可看出,未涂敷和全涂敷目标的RCS计算结果与文献[8]结果一致,只涂敷顶端圆面情况下,在30°之前与全部涂敷目标的RCS差别很小;在30°~60°之间部分涂敷目标的RCS小于未涂敷目标,但是大于全部涂敷目标的RCS;在大于60°时,吸波材料已经不起任何作用了,部分涂敷目标的RCS逐渐与未涂敷目标的RCS重合。
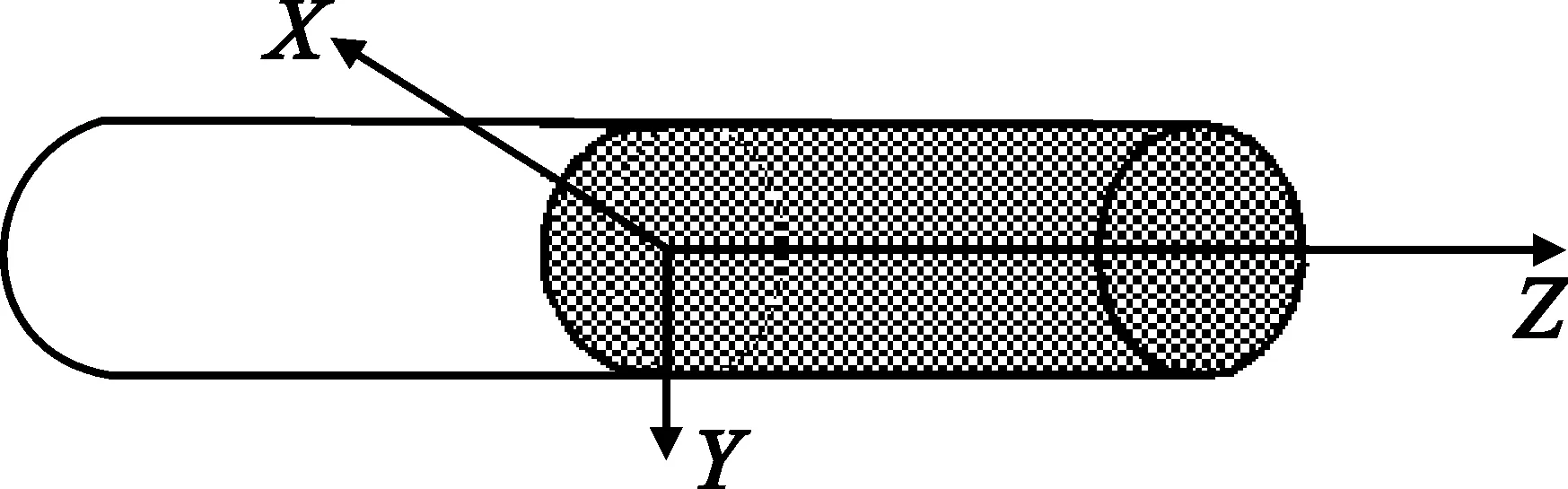
图5 圆柱一半面积涂敷示意图Fig. 5 Geometry of half coated column
从图6可看出,只涂敷一半圆柱情况下,在20°之前与全部涂敷目标的RCS差别很小;在20°~50°之间部分涂敷目标的RCS小于未涂敷目标,但是大于全部涂敷目标的RCS;在大于50°时,部分涂敷目标的RCS远远大于全部涂敷目标的RCS,某些角度上甚至还大于未涂敷目标的RCS。

图6 未涂敷与涂敷圆柱的RCS(一半面积)Fig. 6 RCS of column coated without and with RAM(half area)
4 结 论
在导体目标上部分涂敷雷达吸波材料虽然不能在所有角度上都减缩雷达散射截面,但是在一定的角度范围内起到的作用与目标全部涂敷时相当。所以在实际应用中可以根据需要,适当地给目标部分部件涂敷上吸波材料即可。这样不仅不会影响目标RCS的设计要求,而且还节省了开支。
参考文献:
[1] 阮颖铮. 雷达散射截面与隐身技术[M].北京: 国防工业出版社, 2002.
RUAN Ying-zheng. Radar Cross Section and Stealthy Technique[M]. Beijing:National Defense Industry Press, 2002.(in Chinese)
[2] 施法中. 计算机辅助几何设计与非均匀有理B样条[M].北京: 高等教育出版社, 2001.
SHI Fa-zhong. CAGD & NURBS [M]. Beijing:Higher Education Press, 2001. (in Chinese)
[3] 朱心雄. 自由曲线曲面造型技术[M].北京: 科学出版社, 2000.
ZHU Xin-xiong. Free Curve and Surface Modeling Technique [M]. Beijing:Science Press, 2000. (in Chinese)
[4] Pérez J. Application of Physical Optics to the RCS Computation of Bodies Modeled with NURBS Surface[J]. IEEE Transaction on Antennas and Propagation, 1994, 42(10): 1404-1411.
[5] 吕丹. 基于NURBS建模和PO法的雷达目标RCS仿真研究[D].西安: 空军工程大学, 2007.
LV Dan. Application of PO Method to the RCS Simulation of Radar Targets Modeled with NURBS Surfaces[D]. Xi′an:Air Force Engineering University, 2007. (in Chinese)
[6] 李建辉, 苏东林, 李青. 局部涂敷RAM复杂目标的电磁散射特性计算[J]. 北京航空航天大学学报, 1998, 24(13): 256-259.
LI Jian-hui,SU Dong-lin,LI Qing. Computation of Electromagnetic Scattering Character from Complicated Object Partially Coated with RAM[J]. Journal of Beijing University of Aeronautics and Astronautics, 1998, 24(13): 256-259. (in Chinese)
[7] Klement Dieter, Preissner Jürgen,Volker Stein. Special Problems in Applying the Physical Optics Method for Backscatter Computations of Complicated Objects[J]. IEEE Transactions on Antennas and Propagation, 1988, 36(2): 228-237.
[8] 李建周, 吴昌英, 侯新宇. 基于Unigraphics的雷达截面预估软件设计[J]. 电波科学学报, 2005, 20(2): 222-225.
LI Jian-zhou,WU Chang-ying,HOU Xin-yu. Design of RCS Evaluation Software Based on Unigraphic[J]. Chinese Journal of Radio Science, 2005, 20(2): 222-225. (in Chinese)
