基于正弦曲线拟合算法的ADC测试改进方法*
2010-09-26龙1
桑 龙1,2,陈 静
(1.西北工业大学,西安 710072;2.海军装备部,西安 710054;3.西安科技大学,西安 710054)
1 引 言
模拟数字转换器(ADC)是测控领域经常使用的器件,只有当设计者对ADC器件的设计技巧及其工作特性十分清楚时才可以尽可能地捕捉模拟输入信号中的有用信息,提高检测、监测的精度和速度。传统ADC测试过程往往以直流信号作为检测信号,通过全幅值范围内的测量来获得ADC的特性指标。然而,随着应用领域测量信号速度的不断提高,以往以静态测量为主的测试办法已经不适宜现在的测量过程[1-3]。
正弦曲线拟合方法常用于数据识别过程,其基本思想在于识别信号中存在的谐波分量。在IEEE 1241-2000中,正弦曲线拟合的ADC测试方法已被列为标准测试方法。如果正弦曲线的频率未知,可以采用四参数法进行拟合,如果通过测量或者频率发生器已知正弦频率,则可以通过三参数法进行拟合。然而,在实际的测试过程中由于ADC自身的量化误差干扰、采样值之间不独立等因素,使得正常的正弦曲线拟合方法不能够满足现实的应用。
2 ADC动态参数
在数字通信、超声成像等领域,高速ADC的动态参数决定整个系统的可用度。SINAD、SNR、THD、ENOB等在很多情况下成为科研工作人员所关注的焦点。信噪失真比(Signal-to-noise and Distortion Ratio,SINAD)被定义为测试信号有效值与噪声、谐波有效值之比:
(1)
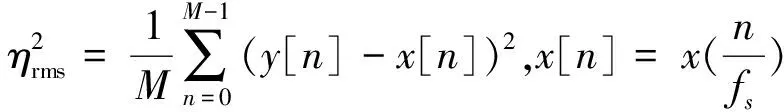
(2)
有效位(Effect Number of Bits,ENOB)的定义式为
(3)
从以上表达式可以看出,对ADC动态参数的测定过程实际上可以表示为对测试正弦激励信号参数进行估计的过程。
3 标准正弦曲线拟合方法
正弦曲线拟合的方法给出全局行为描述。正弦波曲线可以由幅度、频率、相位、偏置电压4个独立参数共同去描述。ADC的正弦曲线拟合方法采用标准正弦信号
x(t)=Acos (2πfit+φ)+C

待估的参数为
P=[Acos (φ),Bsin (φ),C,ω]
(4)
其中:
(5)
式中,ω为待估信号角频率,A、B为待估幅度值,C为待估偏置。在拟合过程中常采用三参数法或四参数法进行估计。如果信号由高精度频率发生器产生或者通过示波器等已知待估信号的频率则采用三参数法,否则利用四参数法进行估计。三参数算法具有闭合、非迭代、运算量少等特性,在工程上经常采用。假设:
ym[A,B,C,ω]=Alcosωltn+Blsinωltn+C
(6)
则其代价函数为
(7)
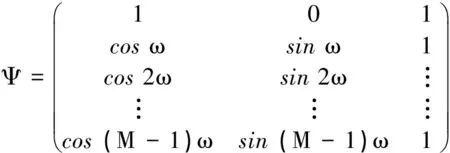
因为Ψ中的列是线性无关的,因此它是满秩矩阵。可以得到:
(8)
通过式(8),就可以推知待测ADC的信噪比、有效位等动态参数。
4 基于Cramer-Rao下界的正弦信号估计
利用最小二乘法进行的估计实际上是在残差的方差最小的情况下取得的,而方差是一个随机变量,η落在它的均值Eη的邻域内的集中或分散程度一个度量,所以一个好的估计量η应该有尽可能小的方差。Cramer-Rao方法可以用于求这个下界。
对于
x(n)=Acos (2πfin+φ)+w[n]
n=0,1,…,N-1;w[n]~N(0,σ2);θ=[A,fi,φ]T,其Fish信息可以表达为
(9)
对其进行简化,对于i=0,1,2,有:
(10)
通过计算有:
(11)
通过对式(10)进行逆运算,可以得到:
(12)
通过式(12)可以看出,对于正弦信号的估计依赖于采样值的大小,当采样次数或者采样频率较大时估计值下限较小。
5 改进型正弦拟合算法
5.1 量化噪声分析
在Widow的量化理论中,量化噪声被设为随机、均匀分布介于±Δ/2间的白噪声,如果该假设成立,则当采样次数足够多时,前述标准正弦曲线拟合方法无疑可以获得较高的测量精度。这就意味着只有当量化区间Δ必须充分小时才可以使得估计成为无偏估计[4]。然而在实际的测试过程中,ADC的量化区间是一定的。图1和图2为理想的3位ADC进行正弦信号测试的结果,可以看出量化误差与输入信号相关,其分布可以被视作由锯齿波信号与正弦的峰值信号共同组成。而正弦的峰值部分恰好反映了待测信号的幅值和直流偏压信号的特性。因此,标准的正弦曲线拟合方法会由于量化误差的引入而造成估计值远大于Cramer-Rao界,拟合出来的曲线幅值会低于原始信号(如图3所示)。

图1 原始正弦信号与量化曲线图Fig.1 The initial sine wave and quantization process

图2 量化误差图Fig.2 Quantization error
5.2 改进算法
正弦曲线的概率密度函数(PDF)为
(13)
可以看出,信号在峰值时误差概率较大。标准正弦曲线拟合算法采用一般意义的最小二乘法进行估计时,忽略了量化误差的非线性成分,将所有的采样数据都视为有效数据。而在正弦的峰值时,量化误差的分布是不均匀的,因此最小二乘法在这里实际上是不适用的。加权最小二乘法从误差分布的角度出发,为每个采样值分配不同的权值,从而可以降低量化误差非线性对估计值的影响。
从式(12)中可以看出,在采样次数一定,误差方差σ2较小时估计的Cramer-Rao界较小,得到的估计值较好。计算估计值的相关函数
同样证明了这个问题。从
可以看出,降低在峰值采样值的权值可以降低估计误差。在这里将量化后采样值进行直方图分析,为每个采样值乘以直方图系数的倒数,得到加权最小二乘法系数。
5.3 仿真结果分析
图3和图4是利用Matlab软件对理想3位ADC进行曲线拟合测试的结果,其中原始测试信号频率为1 MHz,采样频率为5 MHz。可以看出,改进方法的拟合精度远大于标准方法。
从图4可以看出,当测试信号同时施加了加性白噪声时,改进的曲线拟合方法依旧可以给出很好的曲线拟合效果。因此,改进的曲线拟合方法根据式(1)和式(3),能更好地代表ADC嵌入式系统的动态测量效果。

图3 正弦信号以及拟合曲线仿真结果Fig.3 Sine input and the fitting result
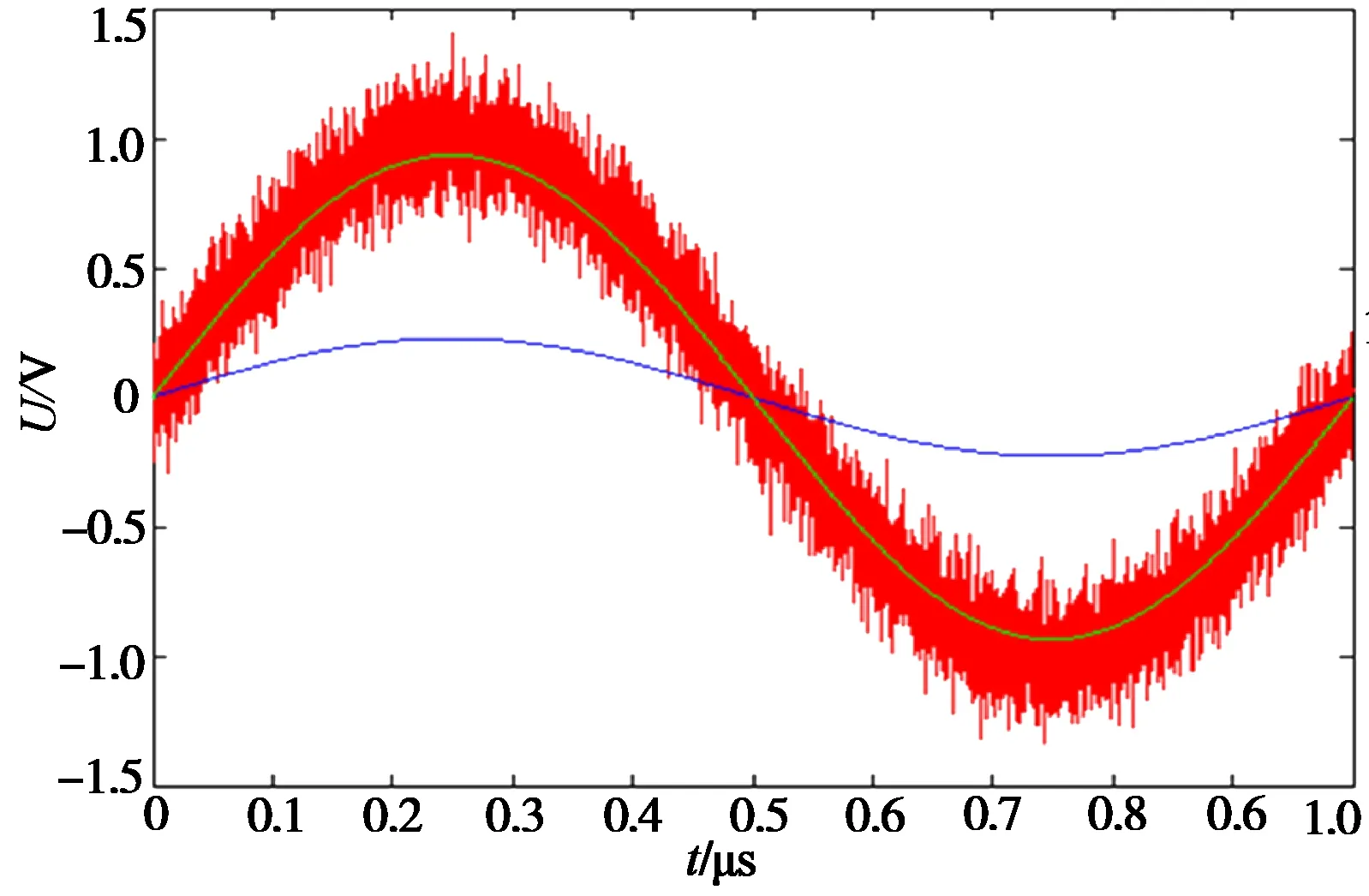
图4 施加了噪声后的信号以及拟合曲线Fig.4 Noise added input and the fitting result
6 结 论
本文讨论了ADC中的动态参数测试正弦曲线拟合方法,并给出了Camera-Rao的正弦曲线估计下界,通过分析找出了引起误差的因素,并利用最小二乘法改进了标准正弦曲线拟合方法。仿真结果表明,该方法可以很好地改进拟合精度,从而提高ADC动态测量参数的精度。
参考文献:
[1] Dallet D,Da Silva J M.Dynamic Characterization of Analogue-to-Digital Converters[M].[S.l.]:Springer,2005:66-69.
[2] Eulalia Balestrieri,Pasquale Daponte,Sergio Rapuano.A state of the art on ADC error compensation methods[J].IEEE Transactions on Instrumentation and Measurement,2005,54(4):1388-1394.
[3] Kollár I,Blair J J.Improved Determination of the Best Fitting Sine Wave in ADC Testing[C]//Proceedings of IEEE Instrumentation and Measurement Technology Conference(IMTC) 2004.[S.l.]:IEEE,2004:829-834.
[4] Attila S′arhegyi,Istv′an Koll′ar.Robust sine wave fitting in ADC Testing[C]//Proceedings of IEEE Instrumentation and Measurement Technology Conference(IMTC) 2006.[S.l.]:IEEE,2006:914-919.
