DS-UWB信号的四阶累积量检测*

(重庆邮电大学 信号与信息处理重庆市重点实验室，重庆 400065)

1 引 言

超宽带技术能够在非合作条件下，检测出超宽带系统中的某些参数或者检测接收到信号信息，对于电子对抗和军事应用具有很重要的意义。直接序列超宽带(DS-UWB)以脉冲极短的脉冲获得超宽的频谱，脉冲占空比很小，使得超宽带信号更加难以检测/截获。直扩超宽带技术具有良好的低功率谱密度发射的隐蔽能力，能在几乎被噪声淹没的功率谱密度下工作，有伪随机编码的保密能力，这些特点都给直扩超宽带(DS-UWB)信号特征参数的估计带来了挑战。有关直扩超宽带(DS-UWB)信号参数盲估计研究，文献[1]中提出了几种检测方法，并提出了分段相关累积(PACA)的方法估计出超宽带信号的相关参数，提出了利用固有模态函数检测方法盲检测DS-UWB信号，这些方法计算都比较复杂，理论上工作的信噪比不是很低。文献[2]利用自相关方法估计出了DS-UWB信号的码片宽度和伪随机序列周期，为了获得-10 dB低信噪比的工作性能，采用分段累积和变换域的方法，自相关方法获得的低信噪比是以增加一定的计算量获得的。

在理论上，高阶统计量能够完全抑制任何高斯噪声，并且包含比二阶统计量更加丰富的信息。根据这些特点，文献[3]提出了一种基于四阶累积量切片检测直接序列扩频信号的方法。根据DS-UWB信号和直扩信号结构上的相似性，本文研究了利用基于四阶累积量切片的方法检测DS-UWB信号。实际上，由于信号的结构差别，基于四阶累积量切片检测DS-UWB信号方法表现一定的差别。最后,根据高阶累积量包含有二阶累积量(自相关)信息特性，分析了利用四阶累积量切片估计DS-UWB信号码片宽度的可行性研究。计算机仿真实验验证了以上分析结果。

2 理论分析

发射直接序列扩频超宽带(DS-UWB)信号波形为[1]

式中，bi是用户的二进制信息序列a的符号，pn∈{-1,+1}表示用户的伪随机序列，Np为一周期内伪随机序列个数，Tp=NpTs表示伪随机(PN)序列周期，Ts表示PN码片宽度，di=bipn表示信息序列a和PN码序列调制的新序列d的符号。Tb=NsTs，每个信息符号由Ns个脉冲组成的脉冲串来表示。

式(2)是高斯二阶导函数波形表达式：

(2)

由高阶统计理论可知，高阶累积量在理论上可以完全抑制任何高斯噪声，二阶统计量并不具备这些性质，因此，应用高阶统计量可以提高抗高斯噪声能力。考虑二元假设检测问题：

H1：x(t)=s(t)+n(t)

(3)

H0：x(t)=n(t)

(4)

式中，s(t)为DS-UWB信号，n(t)为零均值的高斯白噪声，且与s(t)相互独立。根据高阶统计量特性，零均值的高斯白噪声的高阶统计量等于零，即：在H1假设下，得到接收信号x(t)的四阶累积量为

在H0假设下，得到接收信号x(t)的四阶累积量为

c4x(τ1,τ2,τ3)=c4n(τ1,τ2,τ3)=0

(6)

利用高阶累积量的上述特性：高斯白噪声的高阶累积量等于零，混有高斯白噪声的接收信号的高阶累积量等于信号s(t)的高阶累积量，在理论上，使用高阶累积量检测方法能够完全抑制高斯噪声的特性，能够实现低信噪比的检测。但是直接计算四阶累积量需要花费大量的计算量，为了减少四阶累积量估计复杂度和有利于工程实现，可以考虑利用四阶累积量的几种切片作为检测量，以使检测具有应用价值[4]。另外，对称信号的三阶累积量等于零，也就是说对于对称信号，在H0假设和H1假设下都有c3x(τ1,τ2)=0，因此本文选择四阶累积量的切片作为研究对象。

3 基于四阶累积量的检测方法

本文接收信号x(t)假设满足如下条件：

(1)E[s(t)]=0，E[n(t)]=0；

(2)高斯白噪声n(t)和s(t)统计独立。

那么可以得到DS-UWB的四阶累积量为[5，6]

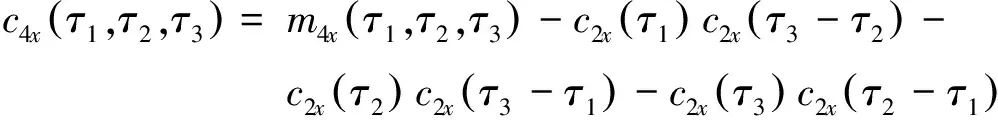
(7)

其中:

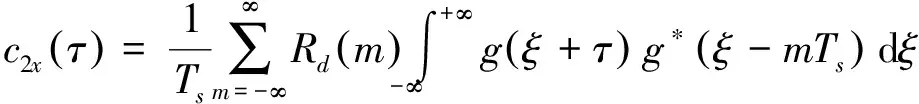
(8)

式(8)就是接收信号x(t)的自相关函数，上标“*”表示信号的共轭运算，m4x(τ1,τ2,τ3)是接收信号x(t)的四阶矩。下面考虑如下接收信号的四阶累积量切片[5]:

当τ1=τ2=τ3=0时，

(9)

当τ1=τ2=τ3=τ时，

c4x(τ,τ,τ)=m4x(τ,τ,τ)-3c2x(0)c2x(τ)

(10)

当τ1=0,τ2=τ3=τ时，

(11)

当τ1=τ2=0,τ3=τ时，

c4x(0,0,τ)=m4x(0,0,τ)-3c2x(0)c2x(τ)

(12)

在一定的虚警概率下，将四阶累积量切片值与门限比较，就可以进行DS-UWB信号的检测。在实际的信号处理过程中，对四阶累积量的有偏估计公式为

(13)

由等式(9) ～(12)对接收信号x(t)的四阶累积量切片c4x(0,0,0)、c4x(τ,τ,τ)、c4x(0,τ,τ)、c4x(0,0,τ)估计之后，与事先确定的门限值TD进行判决，若估计值大于TD，则认为信号存在，小于则认为信号不存在。以切片c4x(0,τ,τ)为例，即：

可以看出，计算特定延迟τ下的四阶累积量计算量比较少。

文献[2]分析了DS-UWB信号的自相关特性，DS-UWB信号的自相关函数存在以码片宽度Ts为周期的周期分量，并利用周期处的峰值准确估计出了DS-UWB信号的码片宽度Ts。从式(7)和式(9) ～(12)中可以看出，四阶累积量及其切片包含了自相关函数信息。在理论上，四阶累积量能够完全抑制高斯噪声，因此，四阶累积量切片方法估计码片宽度具有更好的抑制噪声能力，比自相关估计码片宽度方法要好，利用四阶累积量切片检测方法能实现在较低信噪比时估计出码片宽度。

4 仿真实验

4.1 仿真实验1

本文利用四阶累积量切片检测是利用确定的τ计算出累积量切片值与门限值TD判决的方法。仿真实验中，DS-UWB信号的主要参数：采样频率fc=50×109Hz，信息比特numbits=4 bit，码片宽度Ts=4×10-9s，Ns=32，伪随机序列周期Np=32，脉冲持续时间Tm=1×10-9s，脉冲形成因子tau=0.25×10-9。图1所示是τ3=0，DS-UWB信号的四阶累积量切片图。从图1可以看出，DS-UWB信号的四阶累积量切片当τ=0有最大值，选择τ=0的四阶累积量切片与门限值TD比较可以得到更好的检测性能。

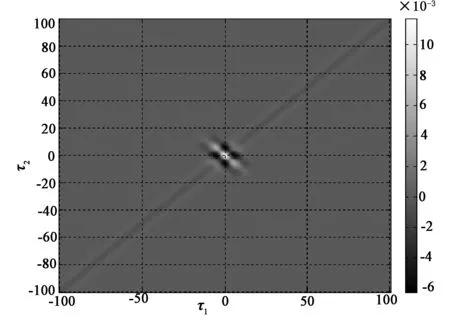
图1 τ3=0，DS-UWB信号的四阶累积量切片Fig.1 Four-order cumulant slice of DS-UWB signal when τ3=0

根据虚警概率为1%设置基于四阶累积量的DS-UWB信号检测门限，检测统计量为c4x(0,0,0)、c4x(τ,τ,τ)、c4x(0,τ,τ)、c4x(0,0,τ)时不同信噪比下检测性能,如图2所示。仿真实验中每个统计量切片的延迟τ=0。从图2中可以看出,四阶累积量2-D切片c4x(0,τ,τ)的检测性能最好，这是因为该切片较充分地利用了伪随机序列的周期特性，同时也能够较好地抑制白噪声。从式(10)和式(12)可以看出，当统计量切片的延迟τ=0时，两个统计量切片估计式是一样的，所以图2所示的检测性能几乎重叠。不同统计量切片延迟τ对用统计量切片c4x(0,τ,τ)检测性能影响如图3所示。图1和图3说明，计算检测统计量切片的延迟τ=0时能够得到最好的检测性能。

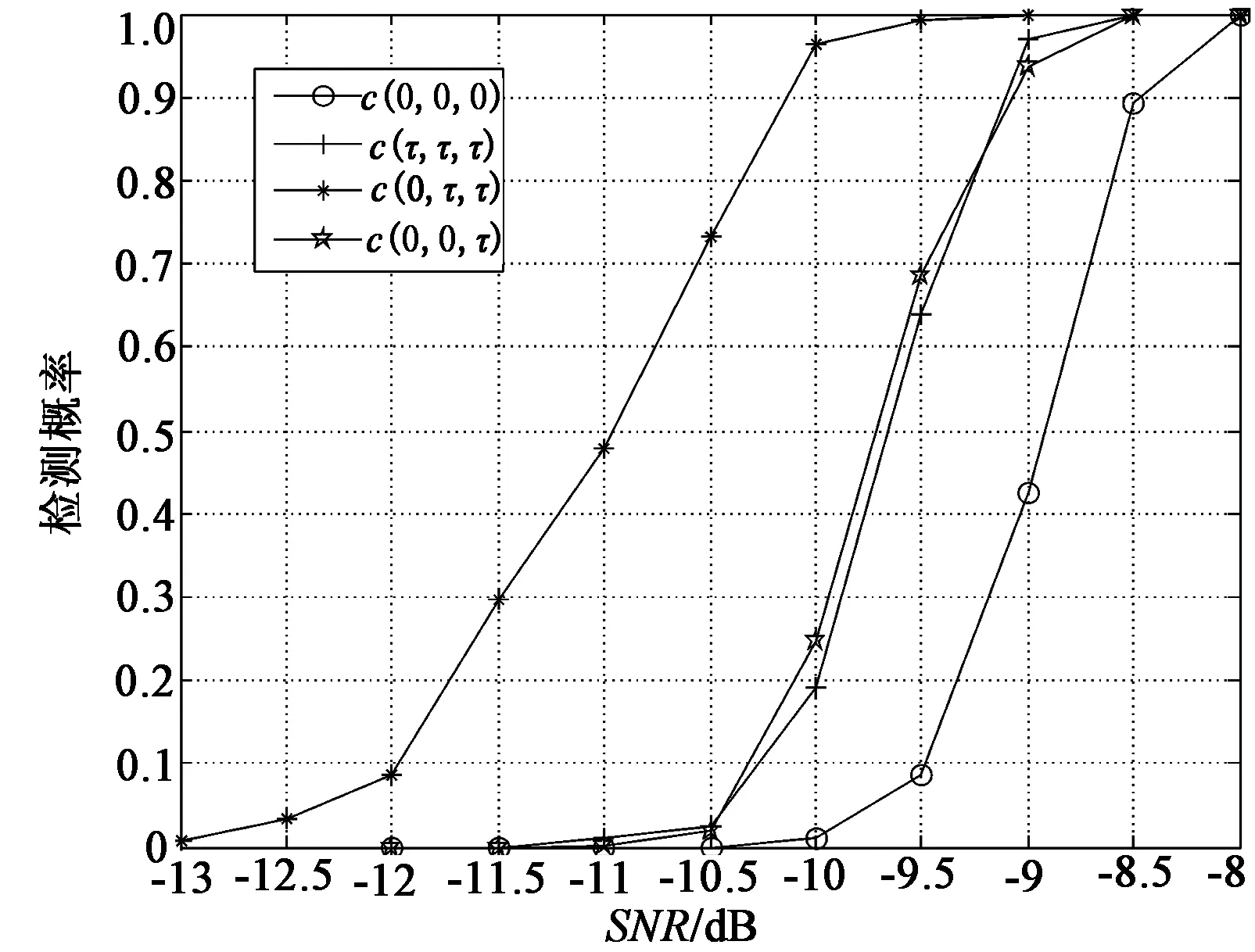
图2 基于四阶累积量的DS-UWB信号检测性能Fig.2 Detection performance of DS-UWB

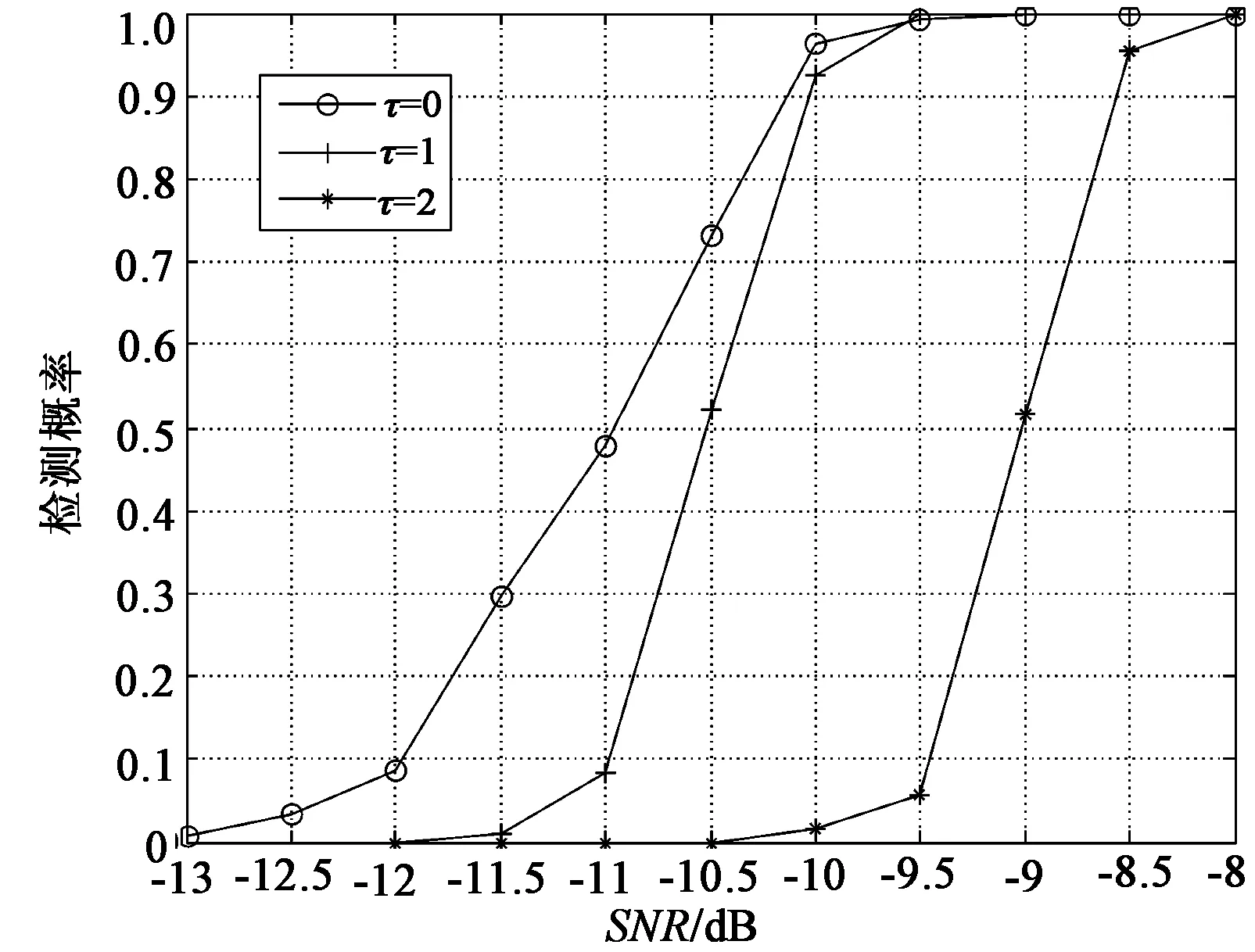
图3 不同τ值对检测性能的影响Fig.3 Effect of differentτon detection performance based on four-order cumulant

无法得到DS-UWB信号的四阶累积量切片的分布，文中门限值TD是根据给定的虚警概率Pf通过10 000次Monte Carlo仿真确定的，从而得到检测概率Pd，由计算机仿真得到基于c4x(0,τ,τ)检测的Pf和Pd的关系曲线(ROC曲线，Receiver Operating Characteristic Curve)如图4所示，说明基于四阶累积量切片的检测方法具有较好的工作性能。

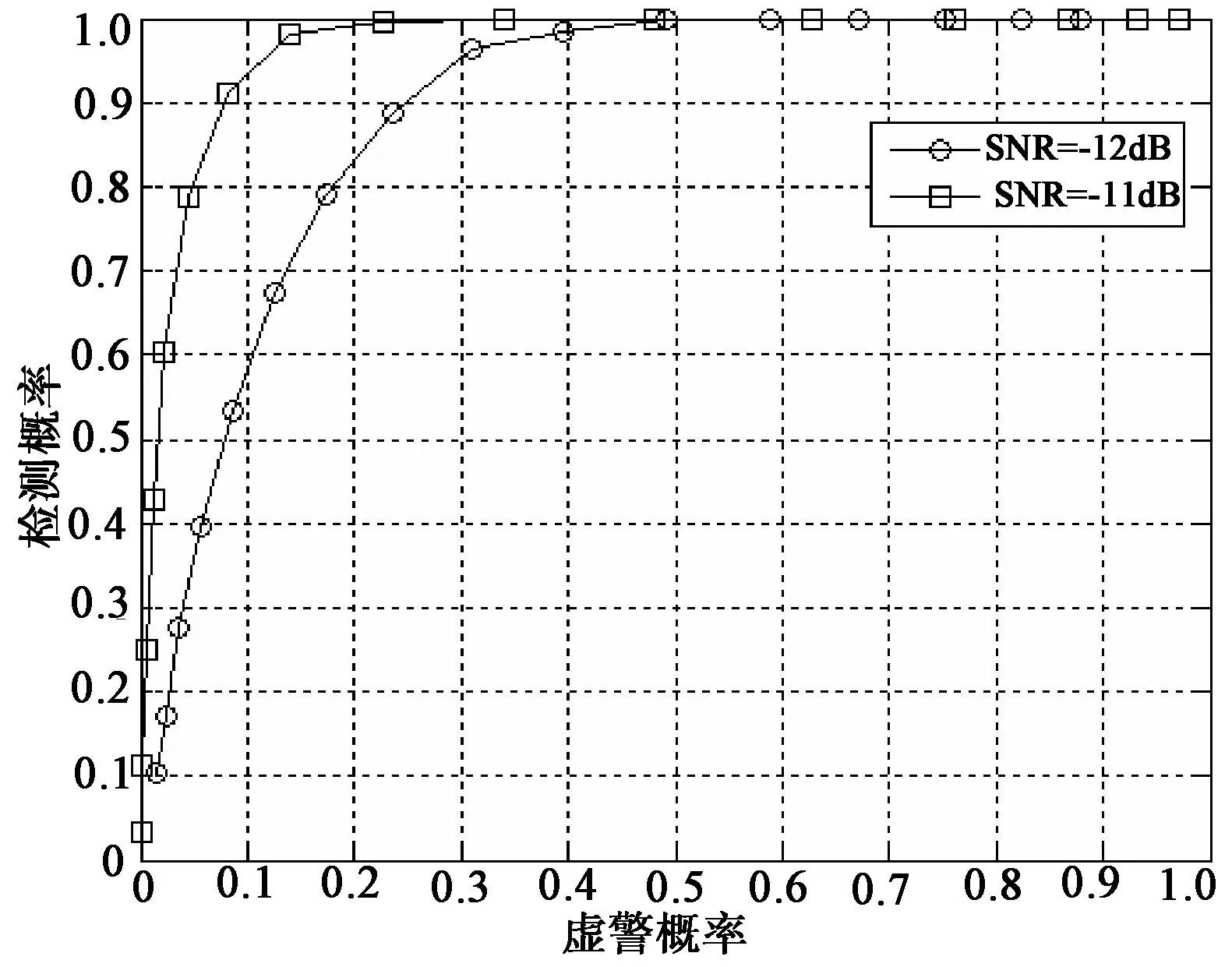
图4 基于c4x(0,τ,τ)检测方法的ROC曲线Fig.4 ROC based on detection method c4x(0,τ,τ)

4.2 仿真实验2

通过实验仿真得出四阶累积量切片c4x(0,τ,τ)估计码片宽度的可行性。图5分别是自相关方法和四阶累计量切片方法的比较。这里信噪比SNR=0 dB。从图5(b)中看出，在fc×Ts=200点的整数倍处出现了峰值，而图5(b)并不是很明显。这说明四阶累积量切片c4x(0,τ,τ)的估计值能够更好地抑制噪声，得到更好的估计效果。为了能够在较低信噪比下估计出码片宽度，文献[2]采用了对自相关值变换频域进行估计，并把接收的信号分成几组求平均的方法，这样就花费了更多的计算时间。本文通过实验的方法得出四阶累积量切片c4x(0,τ,τ)估计码片宽度能够在信噪比-12 dB下工作。

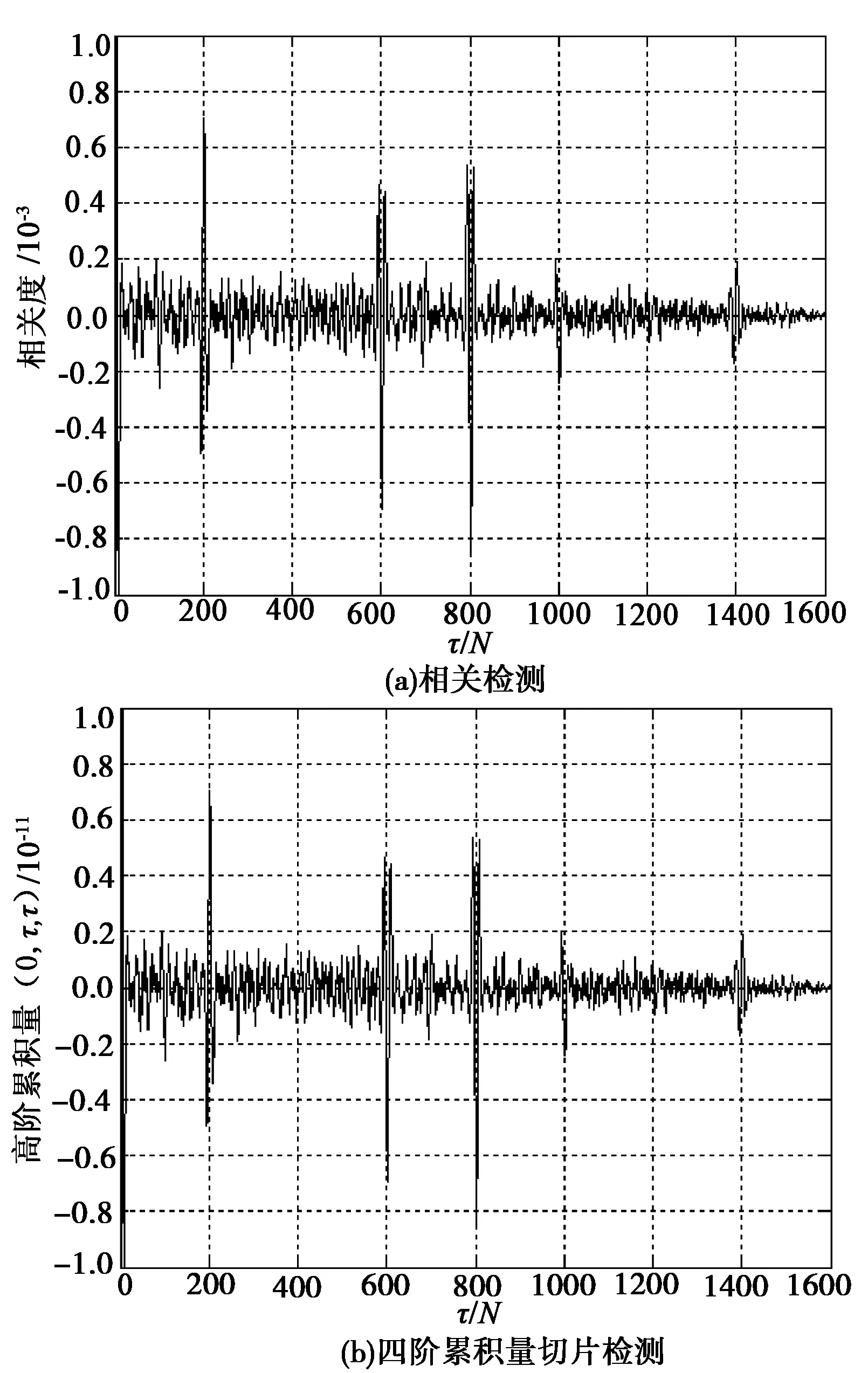
图5 检测性能Fig.5 Detection performance

5 结 论

高阶统计量包含了二阶统计量没有的大量丰富信息，使用功率谱或者相关函数进行分析与处理，而又未得到满意结果的问题可以用高阶统计量处理方法，并可以得到较好的结果。本文分析了四阶累积量切片检测直接序列超宽带(DS-UWB)信号的方法理论，在仿真实验中得出切片c4x(0,τ,τ)在τ=0处能获得最好的检测效果；四阶累积量切片检测码片宽度比相关方法计算量小。实质上，四阶累积量估计参数是利用信号的相关性，本文利用该方法能够估计DS-UWB信号码片宽度，而文献[7]能够估计DS-SS信号的伪随机序列的宽度，这可能是由于信号的结构不同导致了信号相关特性的变化。

参考文献：

[1] 王明阳.非合作超宽带冲激无线电信号检测技术研究学位论文[D].长沙：国防科学技术大学,2006．

WANG Ming-yang. Study of Detection Technology for Non-cooperative UWB Impulse Radio Signal [D]. Changsha:National University of Defense Technology, 2006.(in Chinese)

[2] 杨柳飞，张天骐，李雪松，等.DS-UWB信号参数估计的自相关算法[J].电视技术，2009(4)：60-62，70.

YANG Liu-fei, ZHANG Tian-qi,LI Xue-song,et al. Parameter Estimation of DS-UWB signals Using Autocorrelation Techniques[J]. Video Engineering,2009(4):60-62,70. (in Chinese)

[3] 邬佳,赵知劲.基于四阶累积量的直扩信号检测方法[J].杭州电子科技大学学报,2005(8):50-53.

WU Jia，ZHAO Zhi-jin.Study on Detection method for DSSS/QPSK Signal Based on Four-Order Cumulants[J]. Chinese Journal of Electronics,2005(8):50-53. (in Chinese)

[4] 肖志宇，吕明，唐斌.DSSS/QPSK信号盲检测方法仿真[J].电子科技, 2007(9):41-44.

XIAO Zhi-yu,LV Ming,TANG Bin. Simulation on Blind Detection for DSSS/QPSK Signal[J]. Electronic Science and Technology. 2007(9):41-44. (in Chinese)

[5] 张贤达.时间序列分析-高阶统计量方法[M].北京：清华大学出版社，1996.

ZHANG Xian-da. Time Series Analysis-high-order statistics method[M]. Beijing: Publishing House of Tsinghua University, 2003. (in Chinese)

[6] Maria-Gabriella, Di Benedetto, Guerino Giancda. 超宽带无线电通信[M].葛利嘉，曾凡鑫，刘郁林，等，译.北京:国防工业出版社，2005.

Maria-Gabriella, Di Benedetto, Guerino Giancda. Understanding Ultra Wide Band Radio Fundamentals [M]. Translated by GE Li-jia, ZHU Lin, YUAN Xiao-fang, et al.Beijing: Publishing House of Electronics Industry,2005.(in Chinese)

[7] 沈振惠，唐斌，吕燕，等.基于四阶统计2-D切片的直扩信号多参数估计[J].信号处理，2005(3)：304-306.

SHEN Zhen-hui, TANG Bin,LV Yan,et al.Multiple Parameters Estimation for DSSS Signal Based on Fourth Cumulant 2-D Slice[J]. Signal Processing, 2005(3)：304-306. (in Chinese)