利用多维球形星座映射技术降低终端功耗*

(桂林航天工业高等专科学校 电子工程系，广西 桂林 541004)

1 引 言

4G的实现面临着重大挑战及主要技术问题和障碍，终端功耗问题是4G最需要克服的问题之一[1]。移动终端对功率要求的增长是一个非常关键的问题，该问题会最终决定4G的发展命运。任何终端具有无线能力的一个关键是电池能否给这些终端设备提供足够的电量。对电池过度频繁地充电和更换会使终端及它所提供的服务缺乏吸引力。从4G终端生产商的观点看，功耗问题比较棘手，不仅仅是技术上的原因，还需要考虑市场对新引入技术的期望。对用户来说，终端长时间运行的能力是非常必要的，它可以使用户更好地享受无线服务，而且长时间运行的终端特征已经被消费者列为所有期望需求之首。针对以上功耗来源问题，可以单独从某一个关键技术入手来解决，如芯片设计时的功耗降低处理；通过合作技术来降低功耗[2-5]；天线设计时的极化处理使同一天线通过极化方式转换为多天线等[6]。

为了解决系统单位比特增加、功耗升高的问题，同时保证系统信噪比(SNR)不变，我们提出利用多维球形星座映射来代替立方平面的星座映射技术，从调制映射方面来改善终端的功耗。另外，利用多维星座映射也能够提高系统抗干扰性能。

2 多维星座的最小欧式距离

M-PAM和MASK的星座图是一维的，基于MQAM的OFDM系统采用二维正方形星座，而多维球形星座的信号点分布在以基函数G的各列矢量为基的多维星座图上。可以先将G变换为标准正交基，然后在此坐标系下设计距离特性良好的星座图，就可以将多维星座映射与传统调制方法的星座图映射统一起来，同时，传统的星座图映射方法也都能够为多维星座设计所用，实现差错性能控制[7-8]。

对于M-ASK，信号的最大幅度为

(1)

式中,M是波形的级别数，d是星座图上两个星座点之间的距离。

(2)

M-QAM二维波形叠加后的合成波是信号的最终形式，它的最大幅度是最大正方形的对角线，即:

(3)

此时，取Amax=1，归一化后得到：

(4)

在多维球形星座图中的最小星座点间的距离与平面矩形星座图下两个星座点间的最小距离，通过它们的比值来进行比较，如表1所示，比值大于1则说明球形星座图的性能优于平面矩形星座图。

(5)

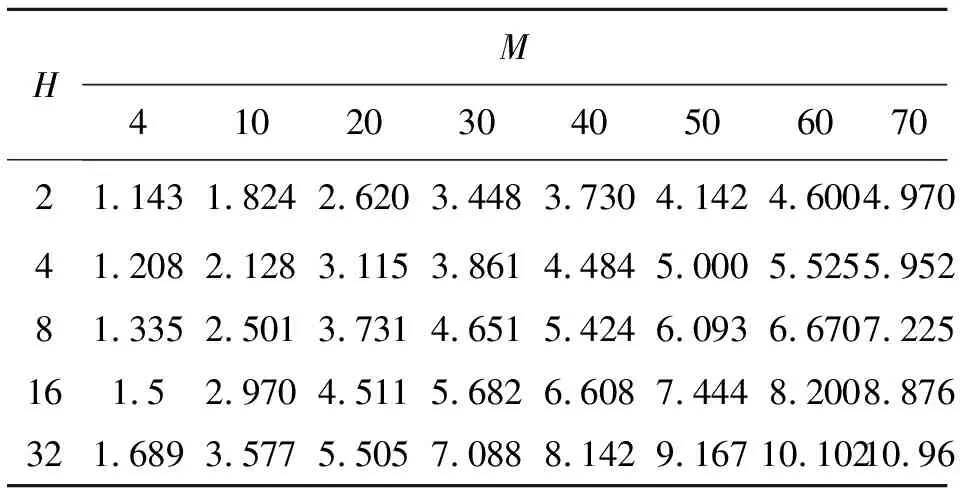
表1 H维球形星座图与立方体星座图M-QAM最小星座距离比βTable1 Minimun constellation distance ratio of H-dimension al constellation and cube constellation M-QAM

从表1和式(5)可得出结论：在相同噪声、携带相同比特数的情况下，基于多维球形星座的M-QAM比基于二维平面矩形星座的M-QAM性能优越。由于星座点的最小距离、发射信号所需能量以及系统抗噪声的能力是一致的，理论上，多维球形星座映射比二维M-QAM、DMT(Discrete Multi Tone)星座具有更优良的性能。即，多维星座映射允许在低的能量消耗和低的信噪比下承载与二维QAM、DMT相同甚至更多的信息量。

3 多维星座误码性能分析

对于二维星座映射，采用M-QAM调制的系统误码率上限为[9]

(6)

(7)

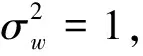
显然，平面星座映射的误码率是较差的，在多维球形星座中，随着维数的增大，误码性能也随着变得更好；但在同一维数的星座映射下，被传输符号的比特数对误码性能影响非常大。随着比特数的增加，系统误码性能下降，但当比特数大到一定程度后，误码性能基本保持不变。

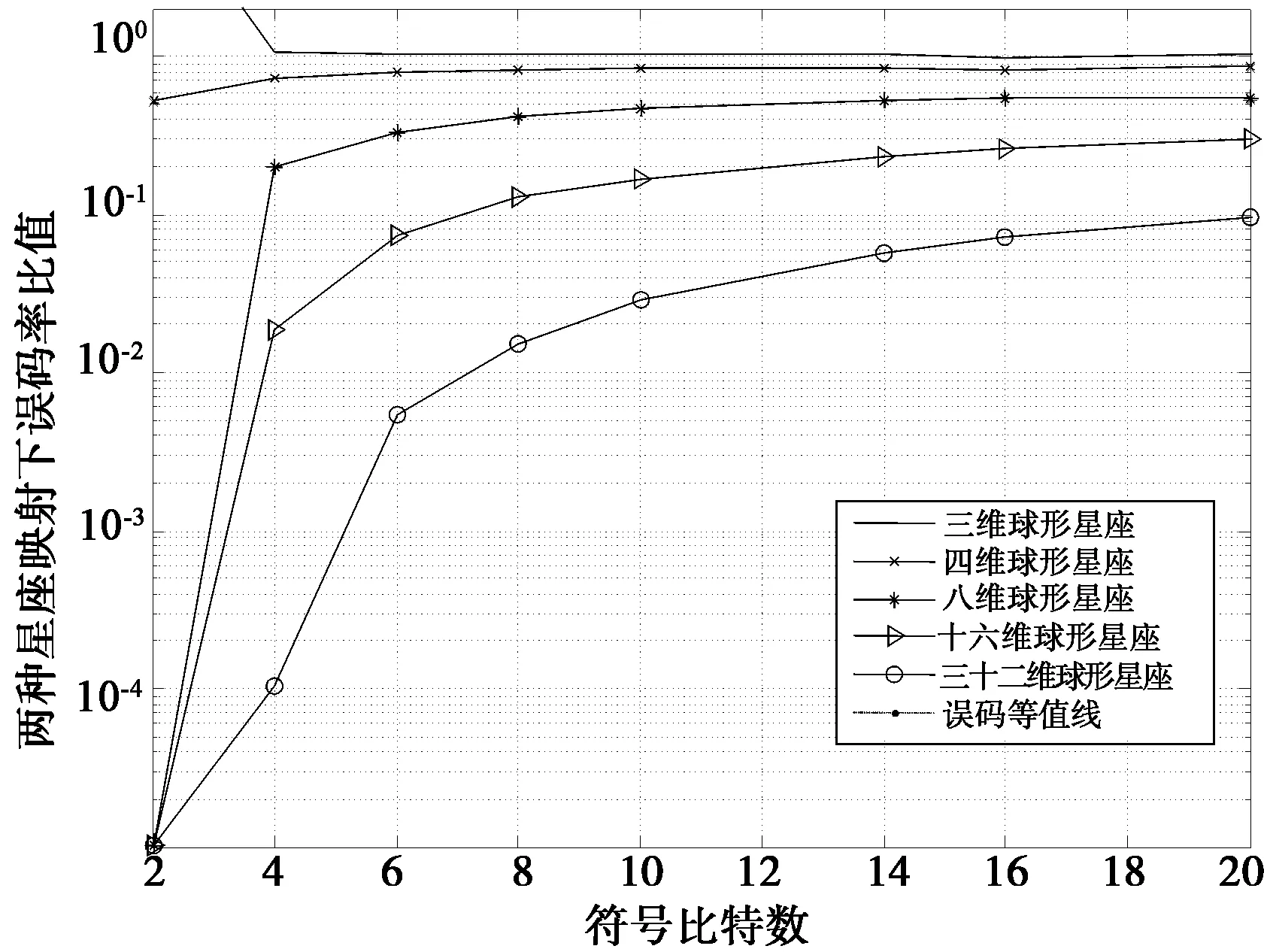
图1 星座距离归一化后的系统误码率比较Fig.1 The BER comparsion of system constellation distance normalized

系统误码率比较的结果与前面得到的最小欧式距离的结论是一致的，即欧式距离越大，系统抗干扰能力就越强。多维球形星座中，星座点的欧式距离明显大于二维星座，所以基于多维球形星座的系统误码性能会更好一些。这个性质在高速传输系统中是非常重要的。

4 多维球形星座映射信号所需能量分析

本节研究在相同情况下，二维星座映射的M-QAM调制方式和多维球形星座映射M-QAM调制方式系统所需要的能量之间的区别，进一步认识多维球形星座映射对4G功耗的贡献。

由文献[7]知，MASK与PAM一样，发射功率的表达式为

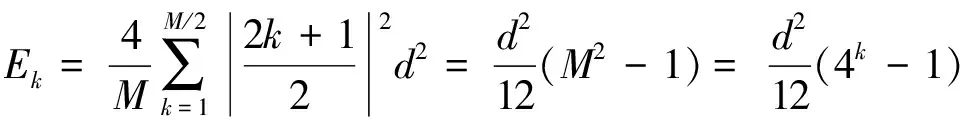
(8)

式中，d为星座图中相邻两个星座点之间的距离，若保持d不变，则每增加一个比特，信号能量变为

(9)

当k比较大时，每增加1 bit，系统至少需要增加4倍(即6 dB/bit)的发射能量。

M-QAM相当于二维的M-ASK，因此可以定义每维平均能量和比特数的关系为

(10)

那么，信号比特总的能量需求为

(11)

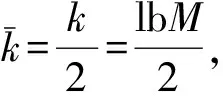
(12)

即系统符号每增加1个传输比特，系统发射能量须增加3 dB。

对于基于H维球形星座映射的MQAM，同理可得：

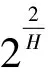
基于上述分析可知：多维球形星座映射在高速数据传输系统中(即k较大时)是所需能量最小的星座映射方式，而且由于其特有的星座图方式，它的抗干扰能力更强。但代价是，若维数H太大，系统增加的复杂度和运算量将会以几何基数增加。

(14)

(15)

而M-QAM在H维球形星座的性价指标为

(16)

图2是多维球形星座和二维平面星座映射条件下系统的星座性价指标曲线。曲线越靠上说明系统性价比越好，二维星座映射性价最低，当H≥3时，球形多维星座的性能要好于平面星座，高维球形星座的星座性价指标是最好的。

图2 多维球形星座和立方体星座的归一化星座性价指标比较Fig.2 The performance comparison of multi-dimensional spherical constellation mapping and cube constellation mapping

5 结束语

把多维球形星座映射技术引入到OFDM系统中，不仅丰富了OFDM系统的调制方法，更重要的是降低了高速率无线通信系统对功耗的需求，为4G系统的发展奠定了很好的理论基础。另外，通过多维球形星座设计，把QAM符号点映射到多维球形空间，系统性能获得了很大的提高。利用星座形状增益换取了系统误码性能的提高，同时降低了终端功率消耗，而这样做的代价是仅仅增加了星座扩张率和系统实现的复杂度。另一方面，也可以考虑采用不规则多维星座设计来进一步达到形状增益和系统复杂度的折衷考虑。

参考文献：

[1] Taylor Ndson Sofres.Two-day battery life tops wish list for future all-in-one phone device[R]. London:TNS,2005.

[2] Katz M，Fitzek F H P. On the definition of the fourth Generation Wireless Communications Networks:The Challenges Ahead[C]//International Workshop on Convergent Technology (IWCT2005).Oulu,Finland：[s.n.],2005.

[3] Niebert N, Schieder A, Abramowicz H,et al. Ambient networks: An architecture for communication networks beyond 3G[J].IEEE Wireless Communications,2004,4(6):312-322.

[4] Politis C,Oda T, Dixit S,et al. Cooperative networks for the future wireless word[J].IEEE Communications Magazine, 2004, 42(9):70-79.

[5] Rhee S,Seetharam D,Liu S. Techniques for minimizing power consumption in low data-rate wireless sensor networks[J].IEEE Wireless Communications Conference,2004,3(3):1727-1734.

[6] IEEE P802.15-04/0137R3,DS-UWB Physical Layer Submission to 803.15 Task Group 3a[S].

[7] 曹祁生,梁德群.非正交多重调制的研究[J].电子学报，2006(1)：19-23.

CAO Qi-sheng,LIANG De-qun.Study on Non-orthogonal Multiple Modulation[J].Acta Electronica Sinica,2006(1)：19-23.(in Chinese)

[8] Forney G D.Multidimensional constellations-Part 11:Voronoi constellations[J].IEEE Journal on Selected Areas Communication,1989,7(6):941-958.

[9] John G Proakis.Digital Communications [M].4th ed.[S.l.]:Mc Graw-Hill Company:276-279.