基于MATLAB软件的船载云台控制系统设计

2010-09-26付强

无线电工程 2010年11期

关键词：开环云台传递函数

付强

(中国电子科技集团公司第五十四研究所,河北石家庄050081)

0 引言

船载云台是船载光学设备的工作平台,其主要功能是保证船载光学设备能够在隔离船摇的平台上完成方位、俯仰方向的搜索和指定位置等工作。其负载经常是长焦、广角摄像机、激光测距机和红外线摄像机等复杂的光学设备,主要应用于港口监管和渔政监督取证等行业。

在这类工程的控制系统参数调试时往往采用试凑法,调试周期长,且调试中激烈的振荡过程会对齿轮箱等造成一定的损害。

MATLAB软件及其环境下的Simulink仿真工具作为当前国际控制界最流行的系统建模、分析和仿真软件,对于稳定控制系统的设计可起到事半功倍的效果。

下面以某型号船载云台的实际设计为例,介绍MATLAB软件及Simulink仿真工具的具体应用。

1 设计方案

1.1 指标要求

船载云台指标要求:云台工作在横纵摇角度达±10°、摇摆周期10 s的船上,负载重量≥80 kg,稳定精度:俯仰:≤0.1°(RMS),方位:≤0.2°(RMS)。

1.2 稳定误差分析

云台安装在船上,伺服系统既要克服船体摇摆,又要保持长期指向目标位置,即必须在陀螺稳定环的基础上再闭合位置环。单纯采用陀螺反馈稳定时,若结构带宽约等于12 Hz,则稳定精度只能在0.3°左右,不能满足指标要求,所以必须增加前馈措施。按照前馈提供3倍隔离度计算,只要使稳定精度≤0.3°即可满足指标要求。

由于陀螺固有的随机漂移及温度漂移特性影响,平台在陀螺环上的长期稳定精度不能达到0.1°,所以要引入倾斜仪和罗经信号并经过适当滤波处理后构成位置环,以达到长期稳定的目的。经过采取上述措施后可以使系统稳定精度满足指标要求。

1.3 控制系统框架

该云台属于船载重型云台,采用方位-俯仰(A-E)型座架结构,光学设备放在俯仰支架上。其控制环路由速度环、陀螺环和位置环组成。

速度环是最内环,由驱动器、直流电机和测速机组成,采用现成产品。

陀螺环在速度环外,由速率陀螺作反馈元件,其控制参数是要调试的重点。

位置环在最外层,由轴角编码装置和倾斜仪构成角度反馈,其控制参数也是要调试的内容。

下面以俯仰轴陀螺环校正参数设计为例,介绍利用MATLAB软件及Simulink仿真工具进行系统建模、设计和仿真的过程。

2 MATLAB软件分析与仿真

2.1 系统建模

给俯仰速度环输入方波信号,通过俯仰陀螺反馈信号确定俯仰机构的传递函数。

根据经验,常常将驱动链(包含速度环及减速机构)的传递函数简化成二阶振荡环节:

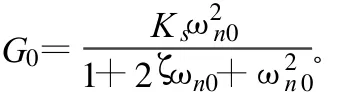
其超调量 Mp和对应的峰值时间tp计算公式为:

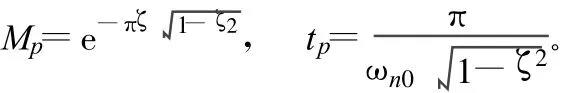
根据测试的相关数据可以得到:Ks=1.5;Mp=0.025;tp=0.098 68。

用MATLAB程序进行计算,可以得到驱动链近似的传递函数G0为:

2.2 MATLAB软件分析

理论分析表明,传递函数为G0的系统要达到稳定精度≤0.3°要求,隔离度需要≥25 dB,即Ks≥31。

通过MATLAB软件做图发现,单纯使用Ks=31进行校正会使陀螺环产生振荡,产生振荡的原因是相位裕度不足,故需要针对相位裕度进行补偿。采取超前滞后校正,其中超前网络形式为:

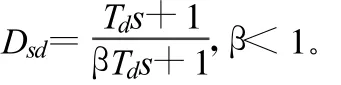
根据G0的特点,拟在 ω=50 rad/s左右产生大约60°的超前角度φ。根据公式:

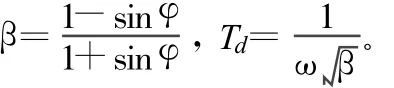
可得到Td=0.066 7。

滞后校正形式为:

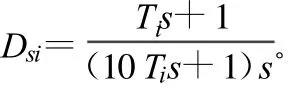
选择 Ti=8Tds,则陀螺环开环传递函数为:G1=。其中Ks=80。

使用MATLAB程序对陀螺环开环特性和闭环特性进行分析、做图,陀螺环开环波特图和闭环阶跃响应如图1所示。

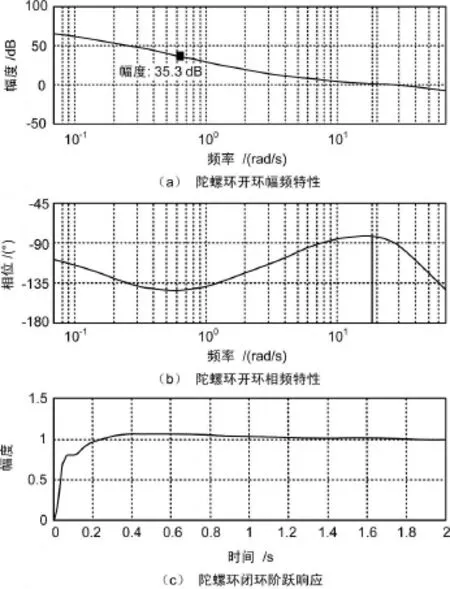
图1 陀螺环开环波特图和闭环阶跃响应

从图1(a)中可见系统隔离度达到35.3 dB,完全满足设计要求。从图1(c)可见阶跃响应满足振荡峰值要求。

使用函数DDs=c2d(Ds,0.01,'tustin')将连续传递函数Ds离散化后即可形成数字化校正公式。由于采样频率很高,不需要做S域到Z域的预畸变处理。

2.3 Simulink工具仿真

针对MATLAB软件设计的传递函数模型及陀螺环、位置环校正参数,利用Simulink工具进行仿真,其仿真框图和结果如图2所示。

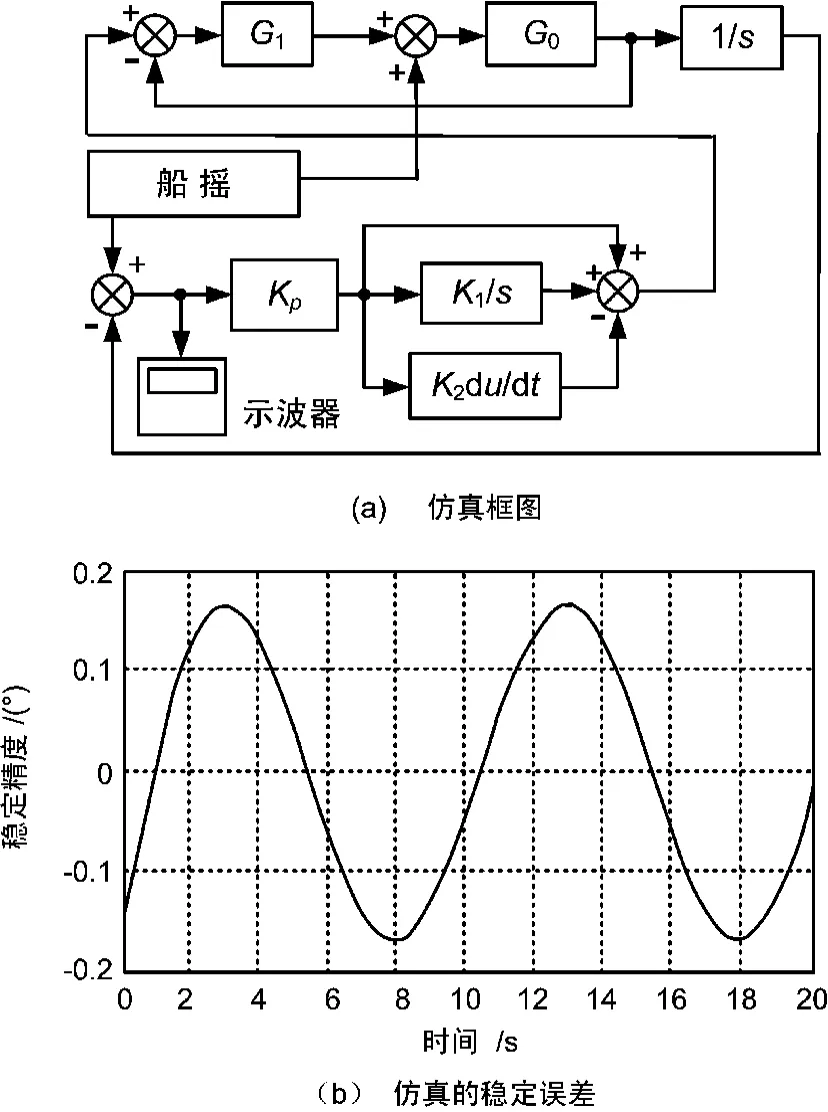
图2 Simulink工具仿真图形

图2(a)为仿真框图,图中上部2个传递函数G0和G1分别为驱动链传递函数和陀螺开环传递函数,加上反馈构成陀螺闭环。图中下部Kp、K1/s和K2du/dt为位置环PID调节器参数,再加上反馈构成位置环。船摇信号发生器产生10 sin(2π/8t)(°)的模拟船体摇摆信号,将它作为给定输入位置环。图2(b)为图2(a)示波器中的稳定误差信号。

从仿真结果可见稳定误差峰值＜0.17°,即稳定精度＜0.12°(RMS),故仿真结果满足指标要求。