关于无穷级数求和的研究及应用

陈文生

(宿迁高等师范学校 数学系，江苏 宿迁 223800)

1 引言及预备知识

无穷级数的敛散性以及求和是高等数学中一个重要而有趣的研究课题，长期以来备受人们的关注。 很多学者做了大量工作，对某些具有特殊通项表达式的无穷级数的敛散性或求和总结出一些规律性的解法(见文献[1]-[4])。 本文从无穷级数部分和的子序列的角度，把级数求和的问题转化数列极限的计算问题，给出了一种判断级数敛散性的方法，并且给出了这种方法在无穷级数求和以及判断级数敛散性中的某些应用。

数列{Sn}的敛散性可由其子列来研究，并且有一个重要的结论。

引理1[5]：数列{Sn}收敛的充分必要条件是{Sn}的任一子列都收敛，且有相同的极限。

特别地，由引理1，可得

引理2： 数列{Sn}收敛于S的充分必要条件是{Sn}的两个子列{S2n}和{S2n-1}都收敛于同一极限。

此时，称两个子列{S2n}和{S2n-1}为互补子序列。

可将引理2推广到一般情形。

定理1： 数列{Sn}收敛于S的充分必要条件是{Sn}的p(p是某个正整数)个子列{Spn}，{Spn-1}，…{Spn-(p-1)}都收敛于同一极限S。

证明 当p=1，p=2时，结论显然成立；下面证明当p=3时结论成立，其他情形类似可证。 由引理1可知“必要性”显然，只要证明“充分性”。 由条件，{Sn}的3个子列{S3n}，{S3n-1}， {S3n-2}都收敛于同一极限S，于是，由数列收敛的“ε-N”定义可得，对任意的ε>0，存在一个充分大的正数N>0，当n>N时，此时n=3k或n=3k-1或n=3k-2，从而有|S-Sn|<ε，故证得数列{Sn}收敛于S。

2 主要结果

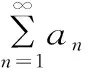
进一步，可将定理2推广到一般情形：

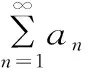
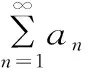
3 结论应用

本小节我们给出子序列方法在无穷级数求和以及判断级数敛散性中的某些应用。

(1)

其中C=0.577216…称为Euler常数，且εn→0(当n→∞时)。对于原级数，并由(1)式可知

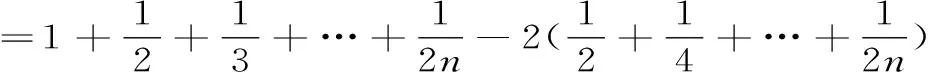
=C+ln2n+ε2n-C-CLNN-εn

=ln2+ε2n-εn→n2(当n→∞时)。

所以，由定理3知，原级数收敛，其和为S=ln2。

例2： 计算

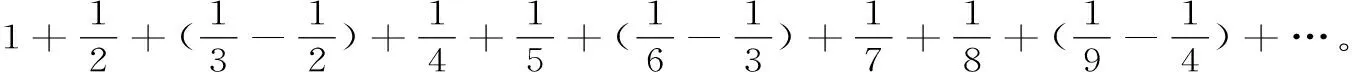
解： 易知此级数通项an→0(当n→∞时)，观察原级数后，考察部分和数列的子列{S3n}的极限。对于原级数，并由(1)式可知

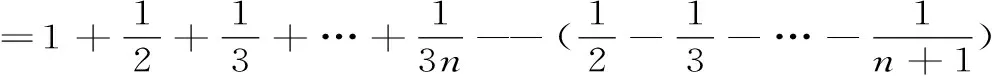
=C+ln3n+ε3n-(C+ln(n+1)+εn-1)→ln3+1(当n→∞时)。

所以，由定理3知，原级数收敛，其和为S=ln3+1。

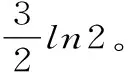
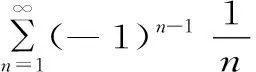
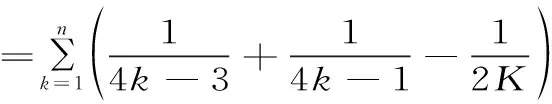
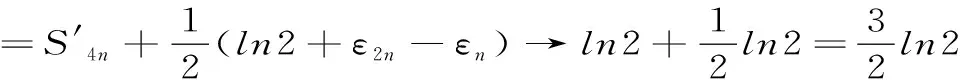
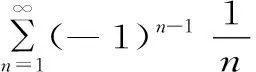
例4： 证明调和级数

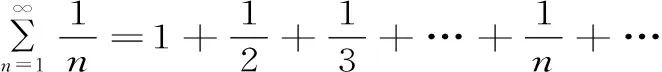
证明： 考察调和级数的部分和数列{Sn}(此时p=1)，并由(1)式知

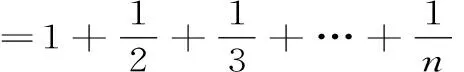
=C+lnn+εn→+∞(当n→∞时，并注意到lnnn→+∞)

故调和级数发散。

例5： 证明级数

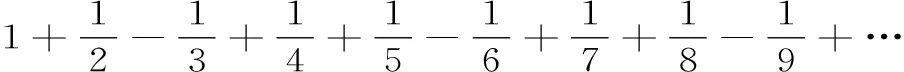
证明： 虽然此级数的通项an→0(当n→∞时)，但它的部分和数列的一个子列{S3n}是发散的。

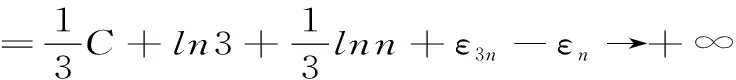
故原级数发散。

通过上述几例我们可以看到，本文所给的子序列方法不仅能够判定级数敛散性，而且能进一步求出一些特殊无穷级数的和。 与现有常用的级数敛散判别法相比，在某些情况下这种方法则更具有优越性。 这是因为，子序列方法是从收敛级数的部分和数列的角度，把级数求和的问题转化为我们所熟知的数列极限的计算问题的。 应该说它是对现有方法的一个很好的补充。

[参考文献]

[1] Bart Braden.Calculating sums of infinite series[J]. Amer. Math. Monthly,1992,99(7):649-655.

[2] Boas R. P.. Partial sums of infinite series and how they grow[J]. Amer. Math. Monthly, 1977, 84:237-258.

[3] 孙珍，李寿贵，张爱丽. 关于无穷级数求和的研究[J]. 数学杂志，2009，29(4)：490-292.

[4] 朱文辉，张亭. P级数的求和[J]. 大学数学，2005，21(3)：114-116.

[5] 华东师范大学数学系. 数学分析:上册[M].2版. 北京：高等教育出版社，1991：43.

[6] 裴礼文. 数学分析中的典型问题与方法[M].北京：高等教育出版社，1993：19-20，338-340.