MATLAB中三个适于数据拟合命令的比较分析
2010-09-25林大伟张宏礼
杨 洪,林大伟,张宏礼
(黑龙江八一农垦大学 文理学院,黑龙江 大庆 163319)
0 引言
在科学数据的处理过程中,常常需要建立变量之间的数学模型。所建立的数学模型往往是非线性的,因为在实际应用中非线性模型常常比线性模型更能反映变量之间的关系。数据拟合是一种重要的建立变量之间数学模型的方法,其求解方法通常是对给定的含有待定参数的数学模型应用最小二乘法求解。随着研究的不断深入,非线性数据拟合问题越来越受到重视。
1 基于最小二乘法的数据拟合
在Matlab下有三个适于数据拟合的命令,它们分别是统计工具箱下的nlinfit()、优化工具箱下的 lsqnonlin()、优化工具箱下的lsqcurvefit(),这三个命令都依据最小二乘法求解[1]。
最小二乘法一般是求解最小二乘问题,最小二乘问题就是对由若干个函数的平方和构成的目标函数求极小值的问题。目标函数一般可以写成
其中,x=(x1,x2,…xn)是集合En中的点,一般m≥n。目标函数极小化可以表示成
特别地,当fi(x),i=1,2,…m中至少有一个是x的非线性函数时,称为非线性最小二乘问题。

2 三个命令的算法原理、格式
2.1 nlinfit函数的算法原理
nlinfit()实际上是非线性回归函数,一般用非线性最小二乘法确定回归方程中的系数[3],其基本算法是Guass-Newton法。
Guass-Newton法可以非常方便地求解最小二乘问题。在Guass-Newton法中需要求解牛顿方程
2f(x(k))d=f(x(k))
由Hesse矩阵
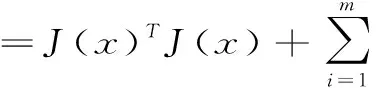
可知,这里需要计算ri(x)(i=1,2,…m),计算量大。为了简化计算,省略Hesse矩阵的第二项,即求解方程组
J(x(k))TJ(x(k))d=-J(x(k))Tr(x(k))
得d(k),然后置
x(k+1)=x(k)+d(k)
这样就得到了Guass-Newton法[4]。
2.2 lsqnonlin函数的算法原理及格式
该函数主要的算法是Guass-Newton法和Levenberg-Marquardt法。
lsqnonlin函数求解非线性数据拟合问题,不仅仅要计算目标函数f(x)(平方和),lsqnonlin函数还需要用户指定函数来计算向量值函数
然后,将优化问题重新写成向量的形式:
式中,x为一向量,F(x)为一返回向量值的函数。
用lsqnonlin函数求解数据拟合问题,其调用格式为:
x = lsqnonlin(fun,x0)
x = lsqnonlin(fun,x0,lb,ub)
x = lsqnonlin(fun,x0,lb,ub,options)
x = lsqnonlin(fun,x0,lb,ub,options,P1,P2,…)
[x,resnorm] = lsqnonlin(...)
[x,resnorm,residual] = lsqnonlin(...)
[x,resnorm,residual,exitflag] = lsqnonlin(...)
[x,resnorm,residual,exitflag,output] = lsqnonlin(...)
[x,resnorm,residual,exitflag,output,lambda] = lsqnonlin(...)
[x,resnorm,residual,exitflag,output,lambda,jacobian] = lsqnonlin(...)
2.3 lsqcurvefit函数的算法原理及格式
lsqcurvefit函数的基本算法与lsqnonlin函数基本相同。同样是应用了Guass-Newton法和Levenberg-Marquardt法。
lsqcurvefit解决非线性数据拟合问题的数学模型为
其中xdata和ydata为向量,F(x,xdata)为向量值函数。
用lsqcurvefit函数求最小二乘意义上的非线性数据拟合问题。即根据输入数据xdata和得到的输出数据ydata,找到与方程F(x,xdata)最佳的拟合系数。
lsqcurvefit求解非线性数据拟合问题。lsqcurvefit需要一个用户定义函数来计算向量值函数F(x,xdata)。用户定义的函数的向量的大小必须与ydata的大小相同。
该函数的调用格式为:
x = lsqcurvefit(fun,x0,xdata,ydata)
x = lsqcurvefit(fun,x0,xdata,ydata,lb,ub)
x = lsqcurvefit(fun,x0,xdata,ydata,lb,ub,options)
[x,resnorm] = lsqcurvefit(...)
[x,resnorm,residual] = lsqcurvefit(...)
[x,resnorm,residual,exitflag] = lsqcurvefit(...)
[x,resnorm,residual,exitflag,output] = lsqcurvefit(...)
[x,resnorm,residual,exitflag,output,lambda] = lsqcurvefit(...)
[x,resnorm,residual,exitflag,output,lambda,jacobian] = lsqcurvefit(...)
3 nlinfit、lsqnonlin和lsqcurvefit命令的实例比较
nilinfit()函数是应用了Guass-Newton法进行求解的,在Guass-Newton法中,当J(x(k))的各列是线性相关,或接近线性相关,换句话说,矩阵J(x(k))TJ(x(k))奇异或是病态的,那么求解线性方程组就会出现一点困难,而lsqnonlin命令是基于Guass-Newton法和Levenberg-Marquardt法进行求解。从而利用Levenberg-Marquardt法设置参数即可完成。已知数据如表1所示

表1 数据表
在Matlab中输入
x=[0.02 0.02 0.06 0.06 0.11 0.11 0.22 0.22 0.56 0.56 1.10 1.10];
y=[76 47 97 107 123 139 159 152 191 201 207 200];
f=inline('p(1)*x./(p(2)+x)','p','x');
[p,r]=nlinfit(x,y,f,[200,0.1])
运行结果为
p = 212.6826 0.0641
r =25.4332 -3.5668 -5.8119 4.1881 -11.3623 4.6377 -5.6848 -12.6848 0.1676 10.1676 6.0319 -0.9681
下面画出由拟合得到的数据及已知的数据散点图。
x1=0:0.02:1.10; y1=212.6826*x1./(0.0641+x1); plot(x,y, 'o',x1,y1)
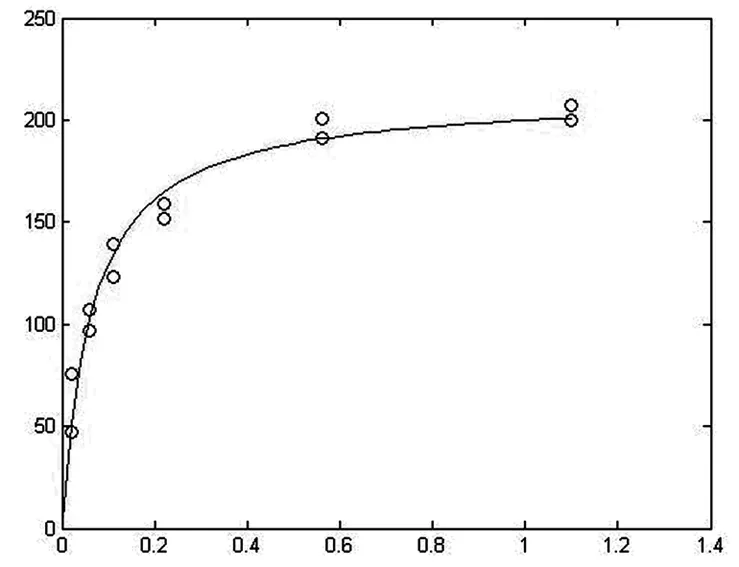
图1利用nlinfit( )数据拟合生成图
在[p,r]=nlinfit(x,y,f,[200,0.1])中,“r”为残差。残差是通过建立的拟合函数求出的值和实际值之间的差值。
下面应用lsqnonlin函数进行拟合,首先编写目标函数 (curve_fun.m)
function y=curve_fun(p)%非线性最小二乘拟合函数
x=[0.02 0.02 0.06 0.06 0.11 0.11 0.22 0.22 0.56 0.56 1.10 1.10];
y=[76 47 97 107 123 139 159 152 191 201 207 200];
y=p(1)*x./(p(2)+x)-y;
再用lsqnonlin()函数求解,输入
[p,resnorm,residual]=lsqnonlin(@curve_fun,[200,0.1])
运行结果为
p =212.6836 0.0641
resnorm =1.1954e+003
residual =
Columns 1 through 11
-25.4339 3.5661 5.8111 -4.1889 11.3617 -4.6383 5.6847 12.6847 -0.1671 -10.1671 -6.0313
Column 12 0.9687
作图如下:
x=[0.02 0.02 0.06 0.06 0.11 0.11 0.22 0.22 0.56 0.56 1.10 1.10];
y1=212.6836*x1./(0.0641+x1); plot(x,y,'o',x1,y1)

图2 利用lsqnonlin ( )数据拟合生成图
虽然lsqnonlin函数较nlinfit函数全面,但在一些基本数据拟合问题上特别在不是解病态奇异的方程组的情况下,应用nlinfit函数与lsqnonlin函数拟合没有明显的差别,几乎可以省略。Matlab用lsqcurvefit函数进行非线性数据拟合,其算法与lsqnonlin函数的算法相同。
4 结语
基于最小二乘法阐述了MATLAB中三个适于数据拟合命令的算法原理、格式,并通过应用实例对这三个命令的异同进行了比较分析。nlinfit()函数实际上是非线性回归函数,其基本原理是Guass-Newton法,它的拟合结果比lsqurvefit()函数的默认控制结果更精确,但是因为其不允许给出像lsqurvefit()函数的精度控制选项,在某方面不能进一步精确。用lsqcurvefit()函数进行非线性数据拟合,设置该函数的目的是提供一个更方便于进行数据拟合的方法,其算法与lsqnonlin()函数的算法相同,都是Guass-Newton法和Levenberg-Marquardt法。但在一些特定的环境不能用lsqnonlin()函数,比如由于大型算法不能求解待定系统,中型算法不能求解有边界约束的问题等,这样的问题应用lsqurvefit()函数更适用更精确些。
[参考文献]
[1] 罗成汉,刘小山.曲线拟合法的Matlab实现[J].现代电子技术,2003,20:16-18.
[2] 薛毅.最优化理论与算法[M].北京:北京工业大学出版社,2004:201-202.
[3] 包翠莲,开小明.Matlab语言在多元线性回归中的应用[J]. 安徽教育学院学报,2005,23(3):55.
[4] 禇洪生,杜增吉,阎金华.Matlab7.2优化设计实例指导教程[M].北京:机械工业出版社,2007:117.
