关于一类特殊非齐次常微分方程的解法

赵 微，许 洁

(1. 大庆师范学院 数学科学学院，黑龙江 大庆 163712；2. 吉林化工学院 理学院，吉林 吉林 132013)

0 引言

在《常微分方程》(文献[1])教材中，对于常系数非齐次的常微分方程，当非齐次项f(t)为两类特殊情况时，即

f(t)=(b0tm+b1tm-1+…+bm)eλt和f(t)=[A(t)cosβt+B(t)sinβt]eαt

时，采用了比较系数法，得到方程的特解，其解法过程中主要是进行代数运算，较为简便。

但对于变系数非齐次常微分方程的解法，常用的方法是先求出其对应的齐次常微分方程的通解，而后利用常数变易法求出非齐次常微分方程的特解，最后得到通解， 由于在常数变易法的过程中，需要计算不定积分，因此计算量大，比较麻烦。

本文旨在给出如下一类特殊非齐次常微分方程

即当方程对应的齐次方程为欧拉方程时，并在非齐次项满足一定条件下，采用比较系数法得到方程的特解，进而求出方程的通解，其过程较常数变易法简便，且计算量小。

1 定理

定理1 考虑方程

(1)

当

f(t)=(b0lnmt+b1lnm-1t+…+bm-1lnt+bm)tλ

时，其特解形式为

证明 做变换，令t=eu，则u=lnt，从而

假设

则

因此，根据数学归纳法，可得到

将上述式子及t=eu代入(1)中，则得到

化简得

合并同阶导数则得到

再将f(t)=(b01nmt+b1lnm-1t+…+bm-1lnt+bm)tλ及t=eu代入上式中，则有

从上式中可看出将原变系数方程化为了常系数方程，且非齐次项满足1)，故可采用比较系数法进行求解。

根据文献[1]，则知上述方程的特解形式为

于是，有

其中λ是对应(1)的次方程的特征值，而k是λ的重数，若λ不是特征值，则取k=2。

再根据欧拉方程的通解形式，则可求得方程(1)的通解。

定理2 考虑方程(1)，当

f(t)=[Acosβ(lnt)+Bsinβ(lnt)]tα，

时，其特解形式为

证明 类似定理1证明，做同样的变量代换，则知，方程可化为

则由[1]知，其特解形式为

其中λ是(1)对应的齐次方程的特征值，k为λ=α+iβ的重数，若λ不是特征值，取k=0。

再根据欧拉方程的通解形式，即可得方程(1)的通解。

2 例证

例1： 求方程t2x″-tx′+2x=tlnt的通解。

解 方程对应的齐次微分方程为

t2x″-tx′+2x=0

是欧拉方程，其通解为

x=C1tcosln|t|+C2tsinln|t|

根据定理1，知其特解形式为

而λ=1不是对应的齐次方程的特征值，故取k=0. 因此特解形式为

代入原方程中，可求得B0=1,B1=0， 故

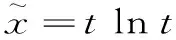
从而原方程的通解为

x=C1tcos ln|t|+C2tsin ln|t|+tlnt

例2: 求解方程t2x″-4tx′+6x=tsin(lnt)。

解 方程对应的齐次方程的通解为

x=C1t2+C2t3

由定理2，知其特解形式为

而不是齐次方程的特征值，故取. 因此其特解形式为

从而原方程的通解为

3 结语

针对一类特殊非齐次常微分方程(1)，运用比较系数法，求得了非齐次方程的一个特解，进而求得非齐次方程的通解。求解过程中直接求解代数方程则可，省去了求不定积分的麻烦，计算量较常数变易法小。

[参考文献]

[1] 王高雄. 常微分方程[M].3版.北京：高等教育出版社，2006.

[2] 丁同仁，李承治.常微分方程[M].北京：高等教育出版社，1985.

[3] 庄万.常微分方程习题集[M].济南：山东科学技术出版社，2004.