非线性系统的RBF神经网络建模方法研究

王艳芹，王凤嫔

(大庆师范学院 物理与电气信息工程学院，黑龙江 大庆163712)

随着控制过程复杂性的提高，控制理论的应用日益广泛。但是，控制理论的实际应用不能脱离被控对象的数学模型。然而，在多数情况下，被控对象的数学模型是未知的，并且在正常运行期间，模型的参数可能发生变化，因此，利用控制理论去解决实际问题时，首先必须建立被控对象的数学模型。这是控制理论能否成功地应用于实际的关键之一。

对于复杂的非线性系统的辨识问题，一直未能很好解决。神经网络所具有的非线性特性和学习能力，为非线性系统辨识提供了新的方法。在动态系统辨识等领域中，多层前向网络的应用极为广泛。但是，大多数基于反向传播学习算法的多层前向网络与参数之间是高度非线性的，网络的学习要基于某种非线性优化技术，于是，都存在一个共同的缺点，即在学习阶段参数估计可能会陷入目标函数的某个局部极小点。虽然对学习算法的改进能在一定程度上避免局部极小，但一般需要大量计算，这将限制多层前向网络的实际应用。径向基函数(Radial Basis Function——RBF)神经网络理论为多层前向网络的学习提供了一种新颖有效的手段[2]。

1 RBF神经网络

RBF神经网络的典型结构如图1所示，不失一般性，假设输出层只有一个结点，这种结构很容易扩展到多输出结点的情形。输入层到隐层为权值1的固定连接。隐含层由一组径向基函数构成，其中对应的中心向量和宽度是RBF的参数。一般隐含层各结点都采用相同的径向基函数，径向基函数有多种形式，通常取高斯函数。隐层的输出在输出层线性加权组合，形成神经网络的输出。

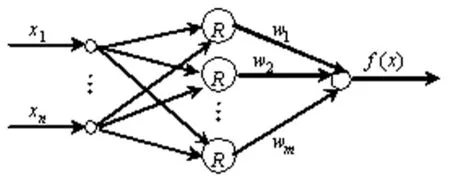
图1 RBF神经网络的结构

网络输入与输出之间的映射关系为:f(x):Rn→R

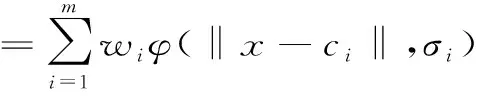
(1)

式中m——隐含层结点数;‖·‖——欧几里得泛数;x,Ci∈Rn；W∈Rm，W∈Rm,W=(w1,…,wm)R；wi—第i个基函数与输出结点的连接权值(i=1,…m)。构造和训练一个RBF神经网络就是要使它通过学习，确定出每个隐层神经元基函数的中心Ci,宽度σi以及隐层到输出层的权值向W量这些参数的过程，从而可以建立所研究系统的输入到输出的映射。

2 RBF神经网络的基本学习算法

RBF神经网络要学习的参数有三个：隐含层基函数的中心、方差以及隐含层到输出层的权值。在RBF网络中，输出层和隐含层所完成的任务是不相同的，因而它们的学习策略也不相同。输出层是对线性权进行调整，采用的是线性优化策略，因而学习速度较快。而隐含层是对作用函数的参数进行调整，采用的是非线性优化策略，因而学习速度较慢。下面阐述RBF网络基本学习方法[4]。

2.1直接计算法

隐单元RBF的中心在输入样本中随机选取，且中心固定。RBF的中心确定以后，隐单元的输出是已知的，这样，网络的连接权就可通过求解线性方程组来确定。

当RBF选用高斯函数时，它可表示为

(2)

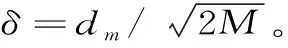
W=G+d,λ=0

(3)

式中，G+是矩阵的伪逆，即

G+=(GTG)-1GT

(4)

其中，G由下式确定

(5)

对于给定问题，如果样本数据的分布具有代表性，此方法就是一种很简单可行的方法。

2.2自组织学习选取RBF中心

在这种方法中，RBF的中心是可以移动的，并通过自组织学习确定其位置。而输出层的线性权则可以通过有导师的学习规则计算。由此可见，这是一种混合式学习方法。自组织学习部分是在某种意义上对网络的资源进行分配，学习目的是使RBF的中心位于输入空间的最重要的部位区域。

RBF的中心的选择可以采用K均值聚类算法。这是一种无监督的学习方法。具体步骤如下：

①初始化聚类中心ti(i=1,2,…M)。一般是从输入样本Xj(j=1,2,…N)中选择M个样本作为初始中心。

②将输入样本按最邻近规则分组，即将Xj(j=l,2，…N)分配给与它距离最近的中心ti所在聚类集合θi(i=1,2,…M)。

③计算聚类集合θi(i=1,2,…M)中的样本均值。得出新的中心ti(i=1,2,…M)。按上述步骤计算，直到中心不再变化为止，否则，转②。

⑤计算矩阵G的各元素。

⑥用高斯消去法求解(3)可求出权阵W。

⑦计算网络输出Y=GW。

由于输出层与隐层之间是线性映射，对输出层权值的计算可以用最小二乘法或高斯消去法求解。

3 RBF神经网络的混合学习算法

RBF神经网络的非线性映射能力体现在隐含层的基函数上，基函数的中心值对RBF网络的非线性逼近能力有很大影响。K均值聚类等方法对聚类的初始类数和位置非常敏感。为此，采用一种优选聚类算法[5]，基于该算法对输入样本的聚类过程进行优化，然后取聚类的组数作为RBF神经网络隐层的单元个数，同时也计算出RBF参数的初始权值。这为进一步精确辨识RBF的参数和网络的权值提供了可靠的基础。为了保证网络具有很好的分类能力和泛化能力，通过调整函数F的阀值，在二者之间进行有效折衷。RBF神经网络中的径向基函数采用高斯函数，故输入层至隐层是非线性映射，采用具有二阶收敛速度的递推学习算法，进一步改善RBF神经网络参数以及权值辨识速度和精度。

3.1 优选聚类算法

为了寻求输入向量样本集的合理聚类结果，给出如下一个控制聚类合理性函数：

(6)

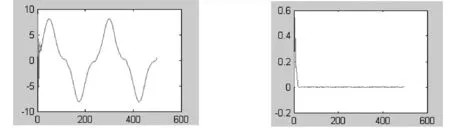
当用适当方法确定规则数m及其中心ci(i=1,2,…m)后，可用上式定量估价聚类的合理性。函数F的意义为：若由聚类划分所形成的同一类中的输入样本靠得越紧，不同聚类中心的距离越远，则聚类结果的合理性越好。聚类的合理性划分就是使函数F越小越好。最邻近聚类法是预先给定一个聚类半径r，置初始聚类个数m=1，取第1个输入样本X1为聚类中心c1，即c1=X1；计算c1与Xp(p=2,3,…,N)的欧氏范数d1p；若d1p为最小者，即d1p=dmin，则作如下判断：若dmin

在上述最邻近聚类法中引入优化策略，用一维寻优方法优选半径r，使式(6)中的函数F达到最小。该算法由半径的优选算法(OA)和聚类算法(CA)两部分组成。CA通过聚类确定类数m和每类的中心ci,i=1,2,…m，然后用式(6)计算函数F的值。OA为主算法，每次迭代均调用CA。OA的基本思路是，先用步长加速法寻求R的最优值rop所在区间，然后用二次多项插值法求取rop。

3.2 RBF神经网络的新型二阶学习算法

采用一种不需任何简化的递推Newton算法，它与Newton法等价，具有二阶收敛速度。

Wm=Wm-1+△Wm

(7)

(8)

(9)

(10)

3.3 仿真实例

以如下非线性系统为例

u(t)=2sin(2πt/250)

进行仿真。采集500组训练数据，首先用优选聚类法得到聚类个数为16个，即RBF神经网络隐层神经元个数为16，则网络结构为2-16-1，其中输入层的输入矢量为XT(t+1)=[y(t),u(t)]。

图2仿真结果 图3相对误差曲线

应用以上混合算法对系统进行仿真。得到仿真结果如图2，相对误差曲线如图3所示。平均相对误差为9.6690E-004。对该非线性系统经过98步训练相对误差达到0.01，而对该系统用带动量项的BP算法达到同样精度需要3845步。由此可见，该混合算法大大提高了收敛速度，节省了运算时间。

4 结语

RBF神经网络为非线性系统建模提供了一条有效的途径。目前用于RBF神经网络的学习算法很多，但算法的收敛性、收敛速度等方面的问题以及用于RBF神经网络学习的新的算法还有待于进一步探讨研究。本文采用RBF神经网络的混合算法对非线性系统进行仿真，结果表明其有效性。

[参考文献]

[1] Jean-Jacques E.Slotine,Weiping Li.应用非线性控制[M].北京：机械工业出版社,2006：1-3.

[2] 高隽.网络原理及仿真实例[M].北京：机械工业出版社,2006：56-57.

[3] Binchini M ,Frasconi P,Gori. Learning Without Local Minama in Radial Basis Function Networks[J]. IEEE Trans. on Neural Networks, 1995,6(3):749-755.

[4] 王永骥，涂健.神经元网络控制[M].北京:机械工业出版社,1998.

[5] 刘铁男. 带优选聚类算法的RBF网络辨识器及应用[J]. 控制与决策, 2003,18(2):233-236.