基于面图标的三维对称张量场可视化研究

宋伟杰， 崔俊芝， 叶正麟

（1. 西北工业大学理学院应用数学系，陕西 西安 710072；2. 中国科学院数学与系统科学研究院, 北京 100080）

基于面图标的三维对称张量场可视化研究

宋伟杰1， 崔俊芝2， 叶正麟1

（1. 西北工业大学理学院应用数学系，陕西 西安 710072；2. 中国科学院数学与系统科学研究院, 北京 100080）

现有的三维对称张量场可视化的面图标方法，仅表现了张量场的某一特征向量场在面图标上的方向信息，而没有表现出特征向量场的大小，基于此，提出了在面图标上通过绘制三维等值线及利用颜色属性来表现特征向量场的大小信息，这样，面图标就将特征向量场的方向和大小信息同时表现出来，从而进一步完善了三维对称张量场的面图标方法，更全面地揭示了张量场位于空间曲面上的信息。

工程图学；可视化；面图标；等值线；对称；张量场

张量场可视化是科学计算可视化的一个极其重要的研究领域，这是因为张量场在物理学、力学和医学等诸多领域中有着非常广泛的应用。例如，固体力学中的应力和应变，流体力学中的应力、粘性应力、雷诺应力、应变率等等都是二阶张量。在医学领域，由核磁共振图像重构得到的扩散张量(DT-MRI)也为二阶张量。因此，深入研究张量场的可视化对于帮助人们理解复杂的物理和医学现象以及揭示其中的科学规律具有非常重要的科学意义。同时，与标量场和向量场相比，张量场更为复杂、抽象，且难以利用已有成熟的计算机图形学技术进行可视化。因此，张量场的可视化一直是科学计算可视化中最具挑战的研究领域，目前研究刚刚起步。二阶张量场中应用最为广泛的一类是二阶对称张量场，而非对称张量场往往可以通过分解转化为对称张量场，因此二阶对称张量场的可视化是目前张量场可视化的研究热点。

目前二阶对称张量场的可视化方法可以划分为两类。一类是采用标量场的可视化方法来实现张量场的可视化，如描绘出张量场的每个分量场的等高线或等值面。这类方法存在的一个致命的缺点是，可视化的结果严重依赖于坐标系的选择，即随着坐标轴的旋转显示的图形也随之发生改变。第二类方法是通过对与之等价的特征向量场进行可视化来实现张量场的可视化。由于特征向量场关于坐标轴的旋转具有不变性，因此可视化的结果不依赖于坐标系的选择。这类方法自提出之后受到了人们的普遍关注，出现了许多经典的可视化方法。这些方法包括基本图标方法[1-7]、基于纹理的方法[8-9]、基于拓扑的方法[10-15]和基于变形的方法[16-17]等。其中，基本图标方法包括点图标方法[1-2,6]、线图标方法[3,5]和面图标方法[4,7]，这3种方法分别在“点”、“线”和“面”的层面上来表现张量场的信息。相对于点图标和线图标，面图标可以在更大的程度上体现张量场的信息和张量场自身的连续性，因而是目前三维对称张量场的一种很有前景的可视化方法。Zhang Song[4]和宋伟杰[7]提出的面图标方法通过构造空间曲面来展现张量场，其中，张量场在空间曲面上的某一特征向量场垂直于该曲面。这样，面图标方法通过空间曲面表现了位于曲面上的某一特征向量场的方向（即垂直于曲面）。由于特征向量场不仅有方向，而且有大小，上述面图标方法仅仅在空间曲面上表现了特征向量场的方向，而没有表现其大小；另一方面，等值线作为科学计算可视化中一种重要的可视化方法，可以直观地反映标量场的分布情况及变化趋势，同时，颜色属性也是一种非常有效的表征标量场大小的手段。因此，本文提出在原有面图标即空间曲面上通过绘制等值线和利用颜色属性来表现特征向量场的大小，这样，在利用面图标表现特征向量场的方向的同时，其大小信息也表现了出来。本文的工作进一步完善了对称张量场的面图标方法，表现了张量场位于空间曲面上的更多的信息。

1 面图标上等值线的生成及颜色属性的设置

面图标方法[4,7]构造的面图标即空间曲面均是采用三角网格来近似表示的，因此，在空间曲面上生成等值线及设置颜色属性的问题就归结为在空间三角网格上的相应问题。

1.1 空间三角网格上等值线的生成

当三角网格顶点的密度较高，即当每个三角片都很小时，可以假定场量函数沿三角片的边呈线性变化。基于这样的假设，在每个三角片内，可以通过对它每条边的两端点处的场量值进行线性插值求出等值线与该边的交点，并将这些交点用直线段连接起来，形成等值线的一部分。遍历所有的三角片，最终生成整条等值线。下面具体给出等值线的生成过程。

1.1.1 判断等值线与三角片的边是否相交

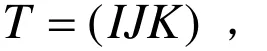
即，当且仅当边 )(IJ的其中一个顶点的场量值大于等于0f，而另一个顶点的场量值小于等于0f时，场量值为0f的等值线与该边相交。当公式（1）中的“=”成立时，等值线通过该边的某个顶点（一个或两个），为统一处理等值线与边相交的各种情况和便于编程实现，将该顶点的场量值暂时增加一个微小的增量ε，这样，等值线通过顶点的情况就可视为与边（内部）相交的情况来处理，同时这种处理方式对生成的等值线的精度影响不大。由于三角片 )(IJKT= 的每个顶点的场量值现在只有大于0f和小于0f两种可能的情况，因此，等值线与三角片的位置关系只有图1所示的八种情况。

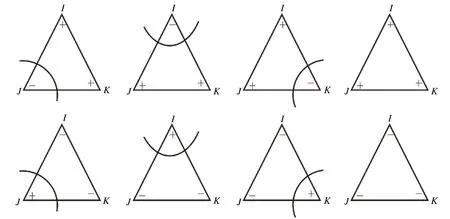
图1 等值线与三角片的八种位置关系。其中，顶点处的“+”和“-”分别表示该顶点的场量值大于f0和小于f0

如果将等值线的值和三个顶点的场量值的大小关系颠倒过来，那么等值线与三角片三个顶点之间的拓扑关系不会改变，生成的等值线是相同的，这样上面的八种情况就可以视为四种情况；再利用三角片的三个顶点存在的旋转对称性，可以进一步将四种情况视为两种情况，即等值线与三角片的两条边相交和等值线不与三角片任何一条边相交。

1.1.2 计算等值线与三角片边的交点

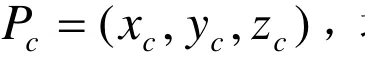
1.1.3 生成等值线

在场量函数沿三角片的边呈线性变化的假设下，公式(2)可以精确地计算出等值线在三角形两条边上的等值点。对于等值线在两个等值点之间的部分，如果三角网格的每个三角片都很小，则可以近似地用直线段连接起来。遍历三角网格的每一个三角片，求出所有的等值线段，这样就生成了整条等值线。

1.2 空间三角网格上颜色属性的设置

等值线可以反映出场量值的分布情况，且等值线之间的疏密程度还反映出场量变化的梯度。如果辅以颜色属性，则可以连续的表现出场量值的大小及分布规律。本文采用通常的蓝色红色颜色变化，蓝色表示较小的场量值，红色表示较大的场量值。将三角网格的每个顶点根据其场量值的大小赋予相应的颜色，每个三角片内各处的颜色则通过对其顶点处已设置的颜色作线性插值得到。

2 实例结果

本例中的三维对称张量场为两竖直向下的外力作用在一正立方体的上表面所形成的应力场。其中，立方体棱长为30mm，材料为钢，弹性模量E=1.93e11Pa，泊松比V=0.29，边界条件为下表面固定，承受载荷为两外力竖直向下作用于上表面中心的两点上，均为600N。

本例采用宋伟杰[7]的面图标方法构造出上述应力场的最小主应力的一个面图标（见图2），然后在该面图标上绘制最小主应力的等值线（见图3）和设置颜色属性（见图4）。为表现最小主应力的实际大小，这里取最小主应力的模的绝对值。

图2 应力场的最小主应力的一个面图标

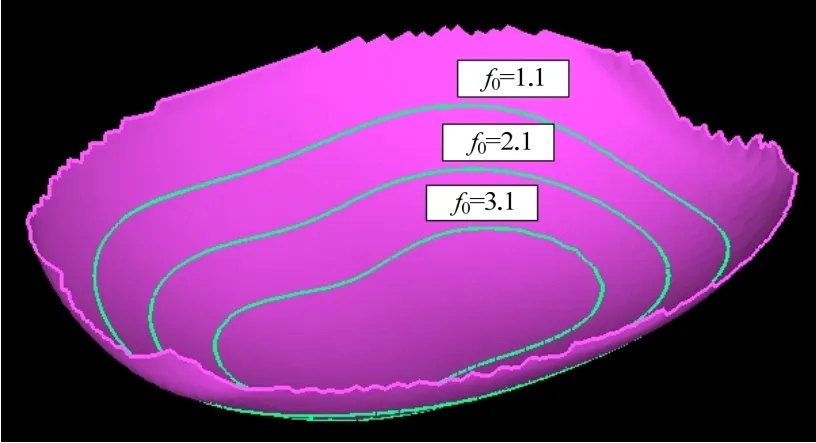
图3 在面图标上绘制场量值分别为1.1、2.1和3.1的三条等值线

图4 在面图标上设置颜色属性

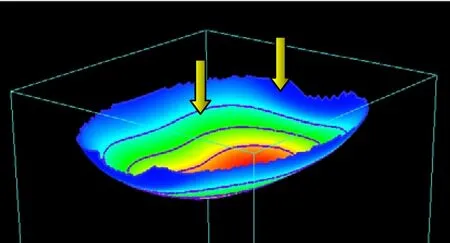
图5 在面图标上同时采用等值线和颜色属性表现最小主应力的大小

由图3～图5看出，面图标作为空间的一个曲面，在表现应力场位于其上的最小主应力的方向（垂直于曲面）的同时，其上的等值线和颜色属性则可以表现最小主应力在面图标上的大小信息。

3 结 论

已有的三维对称张量场的面图标方法采用空间曲面来表现某一特征向量场，与点图标和线图标相比，面图标可以在更大的程度上揭示张量场的内在结构和连续性，但是，现有面图标方法仅仅表现出了特征向量场的方向信息，而特征向量场除了具有方向属性之外，其大小也是一个很重要的信息，因此现有面图标方法所揭示的特征向量场的信息是不完整的。本文提出在已构造的面图标上通过绘制等值线以及设置颜色属性来表现特征向量场的大小，这样，在用面图标表现特征向量场的方向的同时，大小信息也表达了出来。本文工作完善了三维对称张量场的面图标方法，更为全面的揭示了张量场位于空间曲面上的信息。

尽管本文工作完善了面图标方法，使得面图标可以同时表现特征向量场的方向和大小，但是却只能表现其中的一个特征向量场，而对于三维对称张量场来说，有三个特征向量场，因此，研究如何利用面图标同时表现与之相切的另外两个特征向量场是一件非常有意义的工作，这可能需要采用van Wijk的IBFVS方法[19]，至于如何利用该方法来实现将是作者今后研究工作的一个目标。

[1]Haber R B. Visualization techniques for engineering mechanics [J]. Computing Systems in Engineering,1990, 1(1)：37-50.

[2]Kindlmann G. Superquadric tensor glyphs [C]//Proceedings of IEEE TVCG/EG Symposium on Visualization, 2004：147-154.

[3]Delmarcelle T, Hesselink L. Visualizing second-order tensor fields with hyperstream-lines [J]. IEEE Computer Graphics and Applications, 1993, 13(4)：25-33.

[4]Zhang S, Demiralp C, Laidlaw D. Visualizing diffusion tensor MR images using streamtubes and streamsurfaces [J]. IEEE TVCG, 2003, 9(4)：454-462.

[5]陈 莉, 竹岛由里子, 藤代一成, 等. 大规模数据场的并行可视化[J]. 浙江大学学报(理学版), 2001,28(2)：222-226.

[6]Chen W, Zhang S, Correia S. Visualizing diffusion tensor imaging data with merging ellipsoids [C]//IEEE Pacific Visualization Symposium, 2009：145-151.

[7]Song W J, Cui J Z, Ye Z L. Visualizing 3D symmetric tensor fields using a type of surface icons [C]//IEEE CAD/Graphics’09, 2009：627-631.

[8]Cabral B, Leedom L C. Imaging vector fields using line integral convolution [C]//SIGGRAPH, Computer Graphics Proceedings, 1993：263-270.

[9] Zheng X Q, Pang A. HyperLIC [C]//IEEE Visualization,2003：249-256.

[10]Delmarcelle T. The visualization of second-order tensor fields [D]. Stanford University, 1995.

[11]Zheng X Q, Pang A. Topological lines in 3D tensor fields [C]//IEEE Visualization, 2004：313-320.

[12]Zheng X Q, Parlett B, Pang A. Topological lines in 3D tensor fields and discriminant hessian factorization [J]. IEEE Transaction on Visualization and Computer Graphics, 2004, 11(4)：395-407.

[13]Zheng X Q, Tricoche X, Pang A. Degenerate 3D tensors [C]//Visualization and Processing of Tensor Fields, 2006：247-256.

[14]Zheng X Q, Parlett B, Pang A. Topological structures of 3D tensor fields [C]//IEEE Visualization, 2005：551-558.

[15]Schultz T, Theisel H, Seidel H P, Topological visualization of brain diffusion MRI data [J]. IEEE Transactions on Visualization and Computer Graphics, 2007, 13(6)：1496-1503.

[16]Zheng X Q, Pang A. Volume deformation for tensor visualization [C]//IEEE Visualization, 2002：379-386.

[17]Zheng X Q, Pang A. Interaction of light and tensor fields [C]//Proceedings of The Symposium on Data Visualization, 2003：157-166.

[18]Lorenson W E, Cline H E. Marching cubes：a high resolution 3D surface construction algorithm [J].Computer Graphics, 1987, 21(3)：163-169.

[19]Jarke J, van Wijk. Image based flow visualization for curved surfaces [C]//Proceedings of the IEEE Visualization Conference, 2003：123-130.

Research on the Visualization of 3D Symmetric Tensor Fields Based on Surface Icons

SONG Wei-jie1, CUI Jun-zhi2, YE Zheng-lin1
( 1. Department of Applied Mathematics , School of Science, Northwestern Polytechnical University, Xi’an Shaanxi 710072, China;2. Academy of Mathematics and System Sciences, Chinese Academy of Sciences, Beijing 100080, China )

The current surface icon method to visualize a 3D symmetric tensor field just displays the direction of certain eigenvector field of the tensor field, but not its magnitude. The paper presents that rendering 3D isolines and setting color on the surface icons can display the magnitude of the eigenvector field, thus the direction and magnitude of the eigenvector field are displayed simultaneously on the surface icons, which improves the surface icon method of 3D symmetric tensor fields and reveals more completely the information of tensor fields on surfaces.

engineering graphics; visualization; surface icon; isoline; symmetric; tensor field

TP 391

A

1003-0158(2010)06-0146-05

2010-07-13

国家自然科学基金资助项目（10802068）；西北工业大学基础研究基金资助项目（JC200949）

宋伟杰（1977-），男，山西长治人，讲师，在读博士，主要研究方向为科学与工程计算、计算机图形学。

book=150,ebook=151