最大斜度线在图学理论中的合理诠释及应用研究

雷 芳

（福州大学，福建 福州 350002）

最大斜度线在图学理论中的合理诠释及应用研究

雷 芳

（福州大学，福建 福州 350002）

最大斜度线在工程图学中较少研究，其几何定义与作图过程晦涩抽象，但其在建筑设计与工程制图中应用频率很高。对其进行更为确切的定义分析、空间探讨，辅以工程实例的推演及三维可视化表现，有助于深化概念、拓展视野，从而也增强了基础图学理论与后续专业知识的有效衔接。

工程图学；最大斜度线；综合分析；工程应用

最大斜度线是画法几何图学理论中对平面内某一位置直线的定义。其几何模型如图1所示。直线KM属于定平面P，其垂直于P平面内的水平线，且与水平投影面形成的坡度角α为最大。

由于图学理论中几何体主要是以正投影方式体现，求解及作图过程很抽象，如图2所示，需分三个步骤，首先做出平面内的水平线BD的投影，再做直线AE与该水平线的投影垂直，得到最大斜度线的投影ae及a′e′，最后还需用直角三角形法求出其与H投影面的夹角α。作图时一般会产生较大的疑虑，不明白此概念的实际含义，从而与实际运用无法对接，造成一定的局限性。

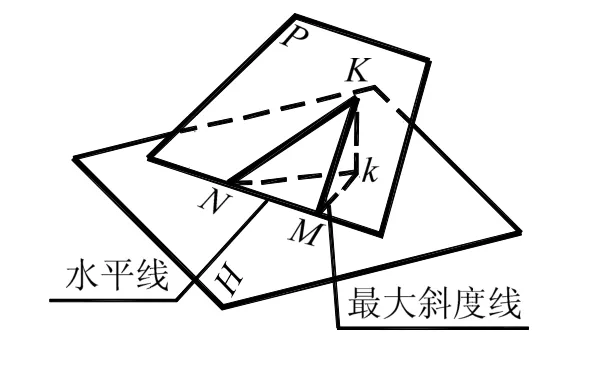
图1 最大斜度线定义

图2 求最大斜度线投影

1 最大斜度线的正确认知

追本溯源，中国图学理论主要是沿袭苏联的体系架构。故理论上确切的解释应为：在任一平面上都可画出无数条方向各不相同的直线，在无数的直线中，有一些是能够完全确定位置的特殊直线如横向平行线、纵向平行线、侧向平行线（图3）。在平面内垂直于此三种平行线的直线，叫平面的最大斜度线（或坡降线）[1]。此坡降线即成为日后土木工程中广泛运用的典型。

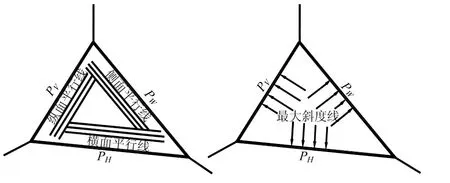
图3 最大斜度线（坡降线）的含义

最大坡降线的物理意义是指位于平面上的小球或水沿着它滚动的那条线。由于画法几何理论最终是通过工程制图将设计思路体现出来的。故概念不清不确切，表达就会有局限性，势必会影响到后续的设计。

第一，对最大坡降线首先不能仅仅以三角面（图4）来定义。将空间扩展后的坡面与三角面拥有共同的最大坡度线。其与地面的交线（迹线）是一条零度的水平线。在工程图中，此一系列的水平线又可称为等高线。那么最大坡度线自然与等高线垂直。

图4 拓展后的最大坡度线

第二，理论上平面内的水平线不是只有一组，更不是只有一条，斜面中水平线的投影可以有很多种表达，并且其所代表的方向不会变（图5），且线和面都是可以扩展的。

图5 在平面中作出水平线的投影

第三，最大坡度线重点不在其长度，关键是其代表了一个最大坡度的方向。由于最大斜度线既不垂直于正投影面也不垂直于水平投影面，故只有将直角三角形转 90°后与水平投影面平行，方可投影得到最大斜度角α，如图6所示，投影作图参见前述图2所示。

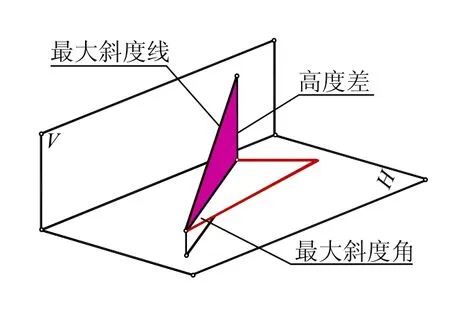
图6 求最大斜度线及夹角

此外，画法几何是一套比较完善的经典图学理论，既有投影分析也有几何论证与计算。最大斜度线的几何架构如下，仅对水平面（O-XY面）而言最大斜度线与水平迹线和法线都垂直[2]其方向矢量为PH=Ai+BCj-(A2+B2)k, 其对O-XY面的倾角θ1

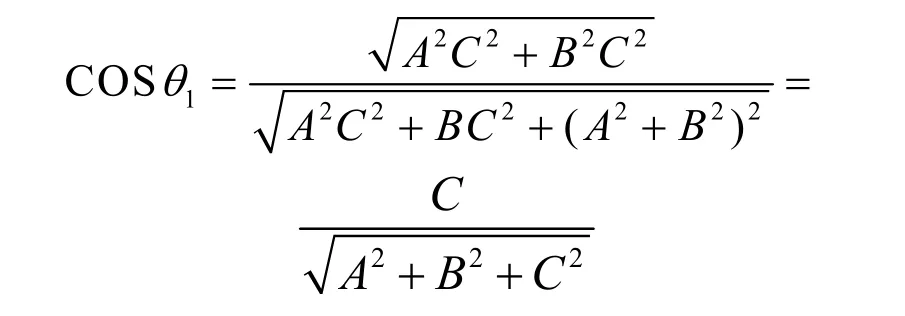
该理论分析的目的主要是为了解决空间定位与定量两大问题，如图7所示。

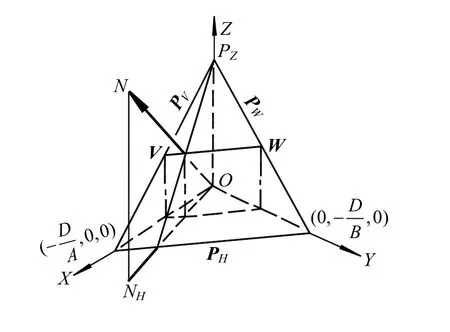
图7 最大斜度线的计算图解

2 最大斜度线的引深与实践

2.1 定位问题

在工程制图中，最大斜度的定位主要是其投影的定位，而确定了最大斜度线，就确立了最合理的平面（或曲面）的坡度角。

如在中国古建筑中大木作斜屋顶或长廊，一般都有斜脊与天沟，其琉璃瓦的铺设总是沿着最大斜度线方向，以利于呈现正确的落水方式如图8所示，注意立面图的投影方向。

图8 长廊屋面最大斜度的投影

在宋清式大屋顶中，最降线的含义是指雨水最快离开屋面，而非雨水离开檐口以后排至最远[3]。最接近理想的速降线如图9中的①，它比直坡屋顶有利于排水，其中清式比宋式更接近理想，更有科学性。

图9 四种坡屋顶线比较

在土木工程中，护坡、围堤、涵洞都有大量的斜坡面出现。最经典的曲面定义为，圆锥上的每一条通过顶点的素线都是最大坡降线，圆锥面自上而下的每个同心圆都是零度的水平圆曲线见图10左图。

图10右图为涵洞渐变段[4]，其造型由方型口渐变到圆型口，正是利用了4个三角形平面与四部分斜圆锥面相切的原理，使曲面过度的坡度最大，最利于引水方向的水流顺畅。

图10 曲面坡度线及渐变段

在具体设计作图过程中，如果已知护坡的坡度角，正立面无积聚现象，那么必须用下列作图来解决，见图11。已知斜面底部水平线投影及平面投影距离，坡度角定为 30°，求立面投影。可先做直线垂直于水平线，然后在水平面画出 30°的直角三角形，将高度坐标差逆推至立面即可得到最大斜度线的立面投影，从而得到坡顶线的投影高度线。

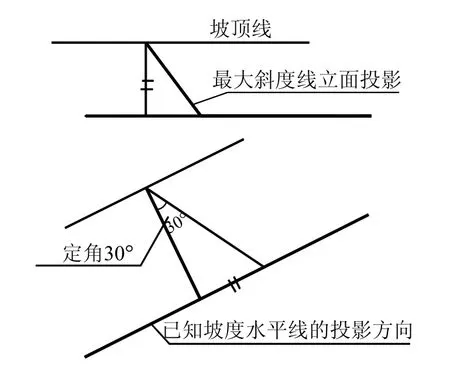
图11 最大斜度线的立面投影定位

2.2 定量问题

定量问题体现在对已有斜面坡的坡角及斜长的确定。前述的直角三角法在实践中最直接的体现在测量的运用，如图 12所示，当竖直度盘对准水平线时刻盘度数为90°，当视线对准P1时得到一角度，则坡度角α=90°-测得的角度。

图12 测量最大坡度角

在交通或水利工程中，为了减少水流的冲刷与腐蚀，最常用的办法就是利用圆锥模拟最大斜度，形成转角护坡斜面。图13中，坡顶B到坡底A的高度差（是定值），半径R=tgα×H，根据受力计算、土石方量与施工要求可推算出一个合理的坡度角α，于是半径R随之确定，以圆锥模拟的最大坡度线成立，作图过程见图13右小图，先做圆锥平面投影弧，再作A点到圆锥底圆弧的切线得水平坡底线，做BC⊥AC，最大坡度方向即确定。

图13 斜面转角护坡

画法几何学的每个概念都是围绕图学理论展开的，而图学理论与专业设计的有效衔接是必然的趋势，作为专业基础知识只有与实际相结合才能体现出知识的连贯性与延伸性。

2.3 经典实例应用

最大斜度线的应用最为成功的实例当属著名华裔建筑师贝聿铭先生设计的位于法国卢浮宫广场上的玻璃金字塔，其高21米，底宽30米，四个侧面由673块菱形玻璃拼组而成，总平面面积约2000平方米。

从图 14中可见，横向、纵向、侧向平行线被巧妙的设计为承重的金属支架，无论从哪个方向看，其最大落水坡度都是最大的，它是现代艺术风格的佳作，也是运用现代科学技术的独特尝试。

图14 贝聿铭作品玻璃金字塔

又如欧洲建筑精粹，郝思拉幼儿园，其建筑体量被划分为很小的结构单元组合，以迎合儿童心理，运用多种不同方向的斜坡屋顶营造出木构建筑的层次感，而且建筑每一层都有通道直接通入户外花园（见图15）。

图15 郝思拉幼儿园

在交通工程中，最大坡度线在开挖线、坡底线及边坡设计中都会用到与最大斜度线为基础的算法及画法。其中一种为人工平面坡，如图16所示，无论挖还是填，只要有一定的坡度定位，其理论依据仍旧是L=tgα×H。当然还需结合力学知识，进行合理的坡度配比，以达到一定的稳定性。

图16 路基工程中的边坡应用

其二是在自然山体中，求路基两侧护坡与自然土壤的交线，如图 16右所示，交线的走向与土坡坡度角以及等高线有着一定的关系，除直线段外，同坡曲面型边坡的出现率更高。且计算中需运用一些插值的手法[5]，以达到一定的精度，如图 17所示。而同坡曲面的引深最终可以达到一个较高的难度，如图 18所示，即随着坡顶的上移，模拟坡度的圆锥呈渐变趋势增大，其法向坡度始终保持恒定，与所有圆锥相切的平面即为所求。水工建筑物拱坝模型均借鉴了最大坡度的概念。

总之，画法几何学为后续土木专业设计的走向提供了坚实的理论依据，研究最基础的点点、线与面的投影及特征，不仅具有一定的教育价值，而且能够更好的服务于工程实践。

图17 自然山体与曲面坡的营造

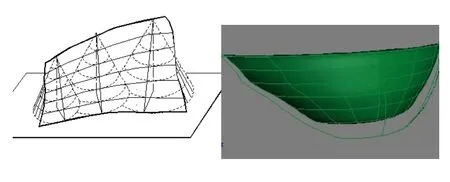
图18 在水利工程中的复杂同坡曲面

[1]A M 叶鲁萨里姆斯基. 画法几何学[M]. 北京：高等教育出版社, 1957. 106-111.

[2]艾运钧. 工程图学分析引论[M]. 北京：中国铁道出版社, 1984. 28-30.

[3]汤国华. 中国传统大屋顶的排雨特点[J]. 新建筑,1996, (4)：65-66.

[4]左 丽. 水工建筑物进出口渐变段直线扭曲面展开技巧[J]. 水利水电技术, 2005, 36(4)：46-47.

[5]方 庆, 徐约素. 画法几何及工程制图[M]. 北京：高等教育出版社, 1991. 235-241.

Study on the Reasonable Annotation and the Application of the Maximum Slope Line in Graphics Theory

LEI Fang
( Fuzhou University, Fuzhou Fujian 350002, China )

The study of the maximum slope line in the engineering graphics is quite less, for its geometry definition and mapping process are abstract and obscure, but it is frequently used in the architectural design and the engineering drawing. The process of carrying out more accurate definition analysis and space discussion, increasing with the engineering examples,three-dimensional visualization will help to deepen the concept, broaden horizons and strengthen the effective convergence of the graphics-based theory and the following expertise.

engineering graphics; the maximum slope line; comprehensive analysis;engineering application

TB 23

A

1003-0158(2010)06-0007-05

2009-09-28

福建省教育厅资助项目(JB07017)

雷 芳（1966-），女，江西萍乡人，讲师，硕士，主要研究方向为工程图学、计算机建筑表现。