关于数学教材(浙教版)节前图设置的实践与研究

何金如

(浙江广播电视大学义乌学院,浙江义乌 322000)

关于数学教材(浙教版)节前图设置的实践与研究

何金如

(浙江广播电视大学义乌学院,浙江义乌 322000)

《义务教育数学课程标准》提倡数学生活化,提倡教学以学生为主体,教材素材应尽量来源于自然、社会与科学的各种现象和实际问题。倡导教师在数学教学中从学生的生活经验和已有知识经验出发,创设生动有趣而恰当的情境,充分激发学生探究欲望和参与情感。

数学教材;节前图;教学情境;实践

一 问题的提出和研究目的及方法

(一)问题的提出

在浙江省普遍使用的浙教版初中数学教材中,每节课都设置了节前图作为情境导入。其中96.77%节前图的情境设置取材于日常生活实例或问题,只有3.23%的情境设置直接来自于数学题。这说明课本中的节前图设置已越来越注重数学生活化。教材中有很多好的节前图情境设置,采用了生活实际场景和问题。但教材中节前图情境设置还存在着一些不足之处,有些偏于形式化,没有考虑情境导入与课程内容上下衔接性;有些开放性太大,难度增强,不能产生应有效果。笔者将从节前图情景设置的理论基础、类型和产生效果、存在问题和修改方案展开课题实践与研究。

(二)研究目的及方法

教学情境是指以直观方式再现书本知识所表征的实际事物或者实际事物的相关背景,是学生认识过程中的形象与抽象、实际与理论、感性与理性以及旧知与新知的关系和矛盾。本文通过对教材中节前图情境设置分类、原则和方法的研究,为课堂教学提供指导和建议改进。

研究方法有:1.文献研究法——通过搜集相关文献资料,阅读、分析、研究情境设置的理论基础以及各类方法,指导本课题的研究;2.文本分析法——采用文本分析法对浙教版《义务教育课程标准实验教科书数学》(7—9年级)中的节前图情境设置进行分类,统计出情境设置所采用方法的比率,并分析各情境设置方法的功能;3.案例研究法——通过选取一些教材中节前图的情境设置,进行分析并提出建议。

二 情境设置理论基础

(一)先行组织者理论

先行组织者简称组织者,是奥苏伯尔20世纪60年代初提出的概念,他解释组织者是先于学习材料呈现之前呈现的一个引导性材料。在概括与包容的水平上高于要学习的新材料,但以学习者易懂的通俗语言呈现,是新旧知识发生联系的桥梁。

若先行组织者用于学生不熟悉的课文中或是采用具体模型的方式,将更有助于学习,因为具体模型直观、形象,通过类比方式能促进学生对新材料的理解,提供给学生缺乏的但又必要的准备知识。同时,在有困难和要求解决的项目上,组织者起概括性提示作用,这也有助于学习、保持和迁移。

(二)建构主义学习理论

建构主义是认知学习理论的新发展,认为知识不是通过感官或交流被动获得的,而是通过认识主体的反省抽象来主动建构的;有目的的活动和认知结构的发展存在必然联系;儿童是在与周围环境相互作用的过程中,逐步建构起关于外部世界的知识,从而使自身认知结构得到发展[1](P103-104),(P250)。

现代建构主义主要吸收了杜威的经验主义和皮亚杰的结构主义与发生认识论等思想。建构主义观下的数学学习具有以下特征:学习不是由教师把知识简单传递给学生,而是由学生自己建构的;学习不是被动接收信息刺激,而是主动建构意义,是根据自己的经验背景,对外部信息进行主动选择、加工处理,从而获得自己的意义;学习意义的获得,是每个学习者以原有的知识经验为基础,对新信息重新认识和编码,建构自己的理解。因此建构主义学习理论认为“情境”、“协作”、“会话”和“意义建构”是学习环境中的四大要素或四大属性,其中“情境”是指学习环境中的情境必须有利于学生对所学内容的意义建构。即建构主义学习理论就是“分析学生学习数学之前人类对数学知识自身的‘建构’过程,并以此为基础来探讨它对数学学习活动和教学活动的涵义”[3]。

(三)情境认知理论

情境认知理论认为知识是具有情境性的,学习只有被放在运用该知识的情境中时,有意义的学习才有可能发生。情境认知强调以学生的生活实际及教学材料为基础,在数学学习中促进学生主动参与、整体发展,并使数学学习生活化。

三 节前图情境设置的类型及产生的效果

根据节前图情境的内容、形式和作用,将其分为:动手操作型、以旧引新型、背景型、问题型、实物型5种情境设置。

对教材中以上5种节前图的情境设置进行统计有155个,它们各自所占比例从图3.1可知:

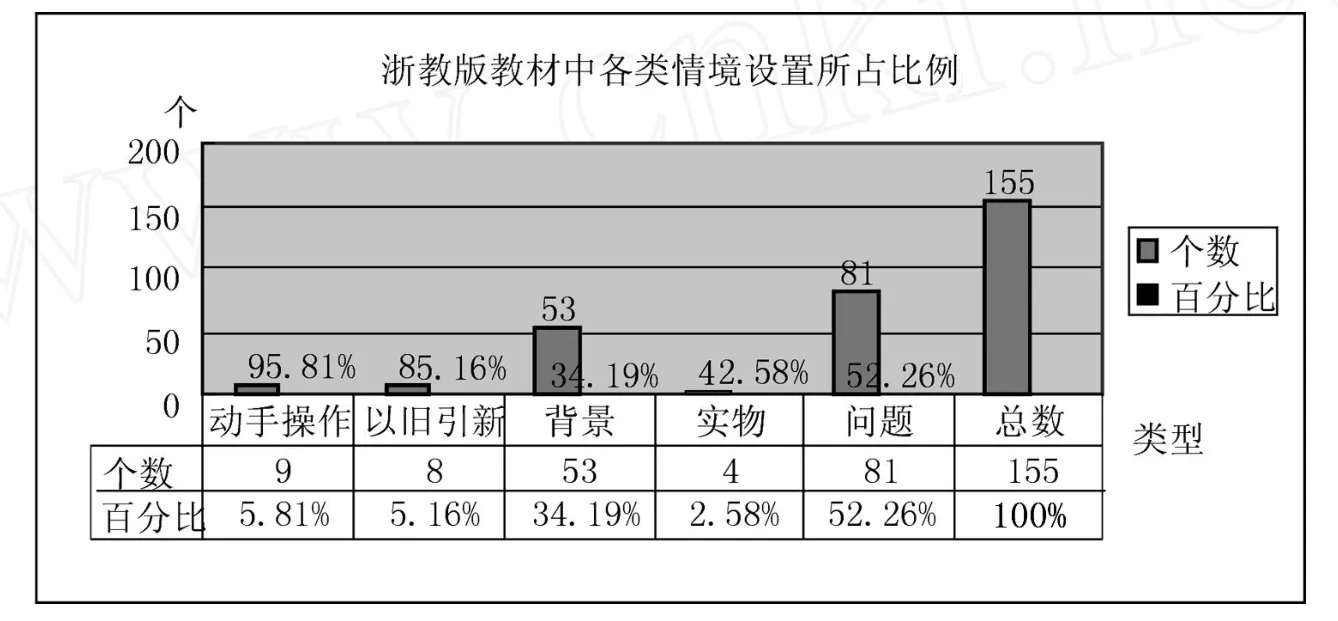
图3.1

教材中问题型情境最多,占52.26%,其次是背景型情境,占34.19%,动手操作型、以旧引新型、实物型情境所占比重不多,分别为5.81%、5.16%、2.58%。下面对155个节前图的情景设置按5种类型进行比较和分析,探讨其优缺点以便促进教学改革。

(一)动手操作型情境设置

美国教育家杜威也曾指出:“让学生从做中学。”因此,根据初中生“爱动”的特点,可在新课导入时采用此类情境设置,让学生自己动手操作,以此激发他们的学习热情,并从中去发现问题,去探索思考问题。

例如“§1.2三角形角平线和中线”(七年级下册)的节前图为:“用折纸的方法可以帮助我们找到三角形的角平分线和中线,试一试。”

本节的教学重点是三角形的角平分线和中线的概念,在新课导入时,运用折纸这个动手活动,让学生尝试着去折出三角形的角平分线和中线,在探索中更好地理解概念,同时为利用量角器、刻度尺画三角形的角平分线和中线做准备。

新课标指出在教学过程中,要以学生为主体,教师起主导作用,同时也指出有效的数学学习活动不能单纯依赖模仿与记忆,动手实践、自主探索与合作交流是学生学习数学的重要方式。著名的现代教学论认为:只有让学生自己经历知识的形成过程,不是在教师指令下默默接受,学生知识和能力才能同时得到发展。有效操作活动以动促思,以思促学,吸引学生真正主动参与到知识形成过程中来,让他们积极进行知识探索[4]。因此,设置良好的动手操作型情境,不仅增加了学生的兴趣,更能很好完成教学任务。

(二)以旧引新型情境设置

学校教学体系是连贯的、完整的、系统性的。在旧知识基础上去学习新知识,能使学生的知识体系具有连贯性,顺利实现知识的迁移。因此,教师可针对教学内容与目标,根据学生已有知识经验,找出新旧知识点的联系,设置以学生已有知识为背景的情境,引导学生实现知识的转化,并培养他们归纳、类比的思维能力。

例如在“§6.1因式分解”(七年级下册)中节前图的情境设置为:“在小学时我们学过怎样把一个整数转化为几个整数的积。在代数中,我们也常常需要把一个多项式转化为几个整式的积。”

这节课的教学目标是了解因式分解的概念和因式分解与整式乘法的关系。为了让学生更好理解因式分解的概念这个新知识点,可通过与小学曾学过的分解质因数概念的类比来帮助学生理解,从数学知识内部入手,达到新旧知识的过渡,便自然而然地导入到新课中。

(三)背景型情境设置

由图3.1可知在数学教材中,34.19%节前图采用生活背景型,以陈述的方式讲解与新课内容相关的生活背景知识,让学生更好理解学习内容。

例如,为了让学生对投影有一个直观了解,在教材“§4.2投影”(九年级下册)的节前图情景设置为:“你看过皮影戏吗?皮影戏就是用灯光将‘影人’投影在幕布上,在艺人的操纵下表演各种动作。皮影戏是中国一种古老的剧种。”

从上述情境中可以看出,皮影戏的介绍不仅能拓宽学生知识面,也能让学生对“投影”的学习产生兴趣。

又如教材“§6.4扇形统计图”(七年级上册)节前图情境设置为:“摩天轮每相邻两根支杆形成的角的顶点都在圆心上,这样的角叫圆心角”。

这是以数学知识为背景的情境设置,圆心角的概念在学生的原有知识库中并不存在,在学习新知识时会产生脱节。有了圆心角的概念,就为新课中扇形统计图的分析奠定了必要的知识基础。

(四)实物型情境设置

教学中的实物型情景主要指实物、模型、标本以及图片等。它能呈现出丰富生动的直观形象,加深学生对知识理解的印象。

在浙教版初中数学教材中,节前图的情境设置都采用图片形式,如“§1.1认识三角形”(七年级下册):在这座塔上我们可以看到很多三角形支架(图3.2)。又如“§3.3三视图”(八年级上册):这是飞机模型(右下)及其从不同方向观察到的视图(图3.3)

图3.2

图3.3

这两节新课都是对图形的认识,图片以直观形象让学生对事物有清楚、深刻的了解。“认识三角形”这一节中,导入时给出三角形的图片,让学生从感官上认识,进而根据自己的感官意识,尝试着给出三角形的定义,从而达到自然引入新课的效果。“三视图”这一节课要求学生具有立体的抽象思维,对一些学生来说具有一定困难,但课本以展示实物图的形式让学生对新课内容有初步认识,对三视图有感性认识,使学生觉得三视图并不难理解,从而唤起他们求知的积极性。

(五)问题型情境设置

问题情境是指个人自己觉察到的一种“有目的但不知如何达到”的心理困境。问题情境就是一种心理状态,一种当学生接触到的学习内容与其原有认知水平不和谐、不平衡时,学生对疑难问题急需解决的心理状态[5](P10-12)。在新课导入时,采用问题情境,设置悬念,因思考问题的过程中会引起学生认知冲突,就能激发学生的探索精神,调动学生的思维活动。

在教材“§4.4方差和标准差”(八年级上册)中,根据方差、标准差在实际生活中的运用,节前图情境设置为:“要选拔射击手参加射击比赛,应该挑选测试成绩中曾达到最好成绩的选手,还是成绩最稳定的选手?”

这样的问题情境,会让学生陷入思考中,但仅凭现有知识则难以解决,因此就会激发起学生想解决这个问题的信心,也就最大限度调动了他们学习的主动性。

图3.4

又如“§5.4一元一次不等式组”(八年级上册)节前图情境为:“某公司从超市购买了墨水笔和圆珠笔共15盒,所付金额超过570元,但不到580元。已知这两种笔每盒的单价如图3.4所示,设购买圆珠笔盒,你能列出几个不等式?”

这又是一个问题情境,在这个情境中给学生描述了公司购买笔的生活场景,购笔也是学生经常经历的一件事,因此他们会有兴趣尝试着去解决疑问。在这节新课之前已经学过一元一次不等式,经过思考,学生能够列出式子。并在节前图所列式子的分析归纳下,学生就会很好地理解什么是一元一次不等式组,并较好地进入到教师的教学活动中。整个过程既启发了学生的思维,让他们自主探索、思考分析,又与教学内容紧密联系,紧扣理解“一元一次不等式组”这个教学目标,同时取材于生活,这些都是问题情境导入所提倡和要求的。

四 现行教材节前图存在问题举例和修改方案

笔者对整个教材中节前图情境设置进行分析时发现,好的节前图确实很多但也存在着一些设置不太合理的节前图,建议进行修改和完善。

(一)案例一

教材“§1.3三角形的高”(七年级下册)节前图情境:“怎样将一块三角形煎饼分成大小相同的六块?”

本节课教学目标是了解三角形高的概念;会画三角形各条边上的高;会利用三角形高的概念,解决有关角度、面积计算等问题。教学重点是三角形高的概念和画法;教学难点是认识直角三角形、钝角三角形各条边上的高。

在整节课的安排中,三角形高的概念是最先提出的,整节课的教学过程都会涉及这个概念并在此基础上加以运用,是本节教学内容的重点。因此作为本节新课情境导入的节前图设置最好能够引出三角形的高的概念,从直观上认识三角形的高,抑或是设置与三角形的高有直接联系的情境导入。

(分析:教材中“三角形的高”这一节的节前图情境设置,此问题要求将任意一个三角形分成面积相等的六块,既然是等分面积,就会想到等分点。因此,会考虑到三角形面积等分可有如下方法,如图:

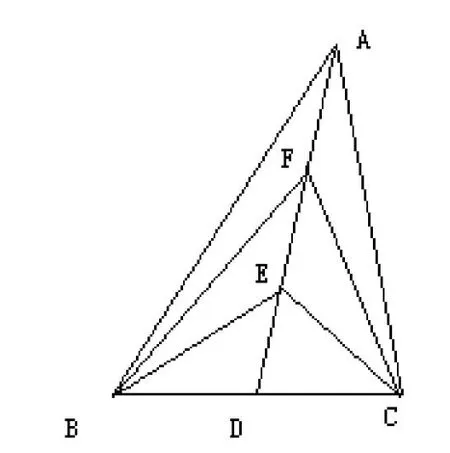
图4.1

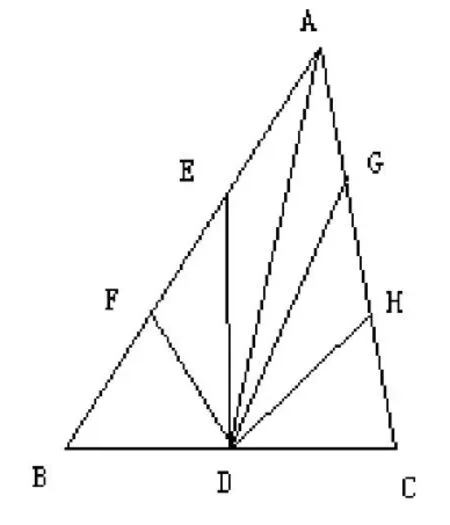
图4.2

图4.3

说明:ΔABC是任意三角形;在图4.1中,点D是边BC的中点,点E、F是线段AD的三等分点;在图4.2中,点D是边BC的中点,点E、F,点G、H分别是线段AB、AC的三等分点;在图4.3中,点D、E、F、G、H是边BC的六等分点。

取等分点的主要原因是考虑三角形的面积计算是底乘高的一半,由于同一边上高相同,于是底的长度也要取相同,把高所在的边等分就能解决问题。

本节课的课题为“三角形的高”,初看到上面这个情景设置,很难想到跟高有何关系,且面积等分一般想到的是中线。此外,此题解题途径和结论都有很大的开放性,因此即使上完新课,这个问题对学生来说仍具有一定的难度。)

根据以上分析,这样的节前图情境难度太大,不是很恰当。笔者给出以下建议:

图4.4

三角形的高是学生在小学阶段已学过的概念,但主要应用在三角形面积的计算,而本节讲述的高的概念侧重于揭示高的内在本质属性。虽然存在差异,但可根据三角形的高的概念的表述作为新旧知识的联系点,采用以旧引新的情境导入,同时,为了使情境设置更贴近生活,可将节前图情境设置修改为:“在工程建筑、机械制造中经常采用三角形的结构,如建造房屋时,有时会先搭建钢架。如图4.4是一屋顶钢架,形状为三角形,你知道如何求出此钢架所围的面积吗?”

我们知道在进行三角形面积求解时,就会想到高,学生就会回忆小学曾经学过的有关高的知识点。根据这些旧知识点,以此来阐述三角形高的概念,便自然而然地引入到整堂新课中,如此修改后的节前图既贴近生活又大大减低了学习“三角形的高”的难度。

(二)案例二

在教材“§4.4整式”(七年级上册)中节前图情境为:“草坪和花圃净化了环境,给人们带来许多美的享受。各式各样的花坛也把城市、街道、住宅点缀得绚丽多姿。”

但本节课的教学目标是了解整式的概念;理解单项式的系数和次数,多项式的项、项的系数及多项式的次数等概念;能确定单项式的次数、系数和多项式的次数。教学重点是单项式、多项式的概念,准确识别单项式的系数、次数,多项式的项、次数与系数;教学难点是确定单项式的系数、次数,多项式的次数。

图4.5

节前图只讲了花坛的美观性,介绍了生活常见景象,与紧接下来的合作学习相互脱节。如果教师按照课本节前图内容导入,上下衔接就很不紧密,或者感觉节前图内容可直接省去的了。

针对以上教学目标及重难点,笔者建议将节前图在原有基础上修改为:“草坪和花圃净化了环境,给人们带来许多美的享受。各式各样的花坛也把城市、街道、住宅点缀得绚丽多姿。如图4.5是一花坛的平面简易图,你能表示出它的面积吗?”

对于修改完善后的节前图设置,学生能很快列出代数式,并且体会到数学知识在生活中的广泛运用,同时与合作学习也有联系,可作为一个具有单项式特征的代数式来归类分析,在此基础上再学习整式的其他内容也就迎刃而解了;同时情景导入针对教学内容,切入点也小。

五 总结

综上所述,通过对现行教材节前图分析和对比发现,五种类型各有长处,如何做到灵活运用要因材施教、因人而宜、扬长避短并有所创新发展。事实证明:教学情境设置有其无可替代的优越性,但教学中也不能太注重情境化,只有合理的情境设置才能起到作用,才能激发学生去探索、解决问题;才能培养学生自主、合作和探究学习方式的培养,提高他们学习数学的积极性;最终实现教学“以学生为主体,教师为主导”的新课标精神。正因为如此,情景设置能使教师当好组织者、引导者与合作者,已成为教师普遍采用的一种教学策略;但是如何更好设置适合学生的情境问题,就成为数学教学一个重要和长期的研究课题。

[1]皮连生.学与教的心理学(第四版)[M].上海:华东师范大学出版社,2004.

[2]张奠宇,宋乃庆.数学教育概论[M].北京:高等教育出版社,1997.

[3]谢明初.数学教育中的建构主义:一个哲学的审视[M].上海:华东师范大学出版社,2006.

[4]许春.让数学课堂焕发活力[EB/OL].http://www.360doc.com/content/090319/09/117009_2853116.html,2010-11 -01.

[5]毕华林,元英丽.化学教学中问题情境的创设[J].化学教育,2000(6).

(责任编辑:王 珏)

G 633.6

A

1009-9743(2010)04-0108-05

2010-07-20

何金如(1965-),女,汉族,浙江义乌人。浙江广播电视大学义乌学院数学讲师。主要研究方向:应用数学。