基于遥感数据随机模型的空间结构分析与蚀变信息提取
2010-09-23张远飞袁继明朱谷昌吴德文
张远飞,袁继明,朱谷昌,吴德文,李 红,3
(1.有色金属矿产地质调查中心,北京 100012;2.桂林矿产地质研究院,桂林 541004;3.中南大学,长沙 408309)
基于遥感数据随机模型的空间结构分析与蚀变信息提取
张远飞1,2,袁继明1,朱谷昌1,吴德文1,李 红1,3
(1.有色金属矿产地质调查中心,北京 100012;2.桂林矿产地质研究院,桂林 541004;3.中南大学,长沙 408309)
遥感图像信号属于随机信号,其波段数据直方图与二维散点图分别是随机模型一维、二维概率密度函数的基本估计。从遥感数据的随机模型出发,讨论了一维概率密度的基本类型与形态、二维高斯分布的椭圆几何参数特征等。在此基础上,系统分析了由不同类型直方图生成的二维散点图的空间几何结构特征,以及异常信息空间定位等问题。最后,通过应用实例阐述了遥感数据空间结构分析在蚀变信息提取中的重要性与实用性。
遥感数据;随机模型;空间结构分析;蚀变信息提取
0 引言
笔者曾在文献[1]中较为详细地讨论过遥感蚀变信息检测中光谱数据点阵空间的几何结构问题,在文献[2]中阐述了基于光谱数据点阵空间遥感图像的背景、干扰与蚀变异常等3个研究对象的定义、相互关系以及它们的复杂度分析等问题,同时给出了干扰因素类型划分、背景与异常信号子空间估计等的基本准则;另外,还总结了遥感数据在大多数情况下,其二维散点图的几何结构具有单椭圆(线性分布形式)与双椭圆(非线性分布形式)两种基本类型;并在实际工作中使这些研究结果得到了有效的应用[3,4]。但是,在上述文献中仅仅给出了遥感数据几何结构的描述与基本分类,并未涉及两个波段联合概率密度的高斯分布为什么是椭圆形态的数学求证,以及两个不同波段组合的二维散点图会出现哪些空间几何形态等问题。
遥感图像信号属于随机信号,其反映的物理现象随空间坐标而变化,属于典型的随机过程,可采用概率密度函数作为描述它的随机模型,而遥感波段数据的直方图与二维散点图分别是随机模型一维、二维概率密度函数的基本估计;另一方面,遥感的多(高)光谱数据是一种多元数据集合,每一个像元代表的是一个波谱矢量。所以,遥感图像多元数据集合在高维空间中形成一个点阵,这个点阵空间具有一定的几何结构[5]。本文将重点讨论二维点阵空间(即二维散点图)的几何结构特征。
从遥感数据的随机模型出发,讨论一维概率密度的基本类型与形态、二维高斯分布的椭圆几何参数特征。研究表明,遥感波段数据的概率密度分布同其点阵空间中的几何结构有密切关系。基于这个基本前提,系统分析了不同类型二维散点图的空间几何结构特征,以及异常信息空间定位问题;并通过应用实例阐述了遥感数据空间结构分析在蚀变信息提取中的重要性与实用性。
1 单波段直方图与一维概率密度分类
众所周知,一般情况下都假设单波段遥感图像数据的概率密度为高斯分布,又称正态分布,特别是早期的遥感图像处理方面的研究更是如此假定。正态随机变量X的概率密度函数的形式为

式中,μ为随机变量X的均值;σ2为随机变量X的方差。
在实际工作中发现,大量观察到的遥感图像直方图,其形态与参数大多数都很难符合高斯分布的要求。
近年来,随着高阶统计量的研究,发现采用偏度(三阶中心矩)与峰度(四阶统计量)能够分别度量概率密度的均值对称度(分左偏分布与右偏分布)与非高斯性。
根据峰度可以把概率密度分布进行分类[6,7]。一般地,具有负峰度的分布属于亚高斯分布;若峰度为正,则称为超高斯分布。亚高斯概率密度倾向于比高斯密度分布更平坦或者多峰。典型的超高斯概率密度比高斯概率密度函数具有更尖锐的峰和更长的拖尾。遥感图像数据不同概率密度分布的实例可参考文献[1]。
2 二维散点图与二维高斯分布椭圆几何参数特性
2.1 二维散点图与二维概率密度分布
二维散点图又称二维直方图,它表示了2幅图像像元值的组合分布情况[8]。事实上,二维散点图反映的是2个变量的联合概率密度分布的几何形态。图1是青海省黄南州吉地地区TM图像的TM5与TM7两个波段的直方图及其二维散点图,由于这2个波段基本接近高斯分布,它们的二维散点图近似于椭圆形态。
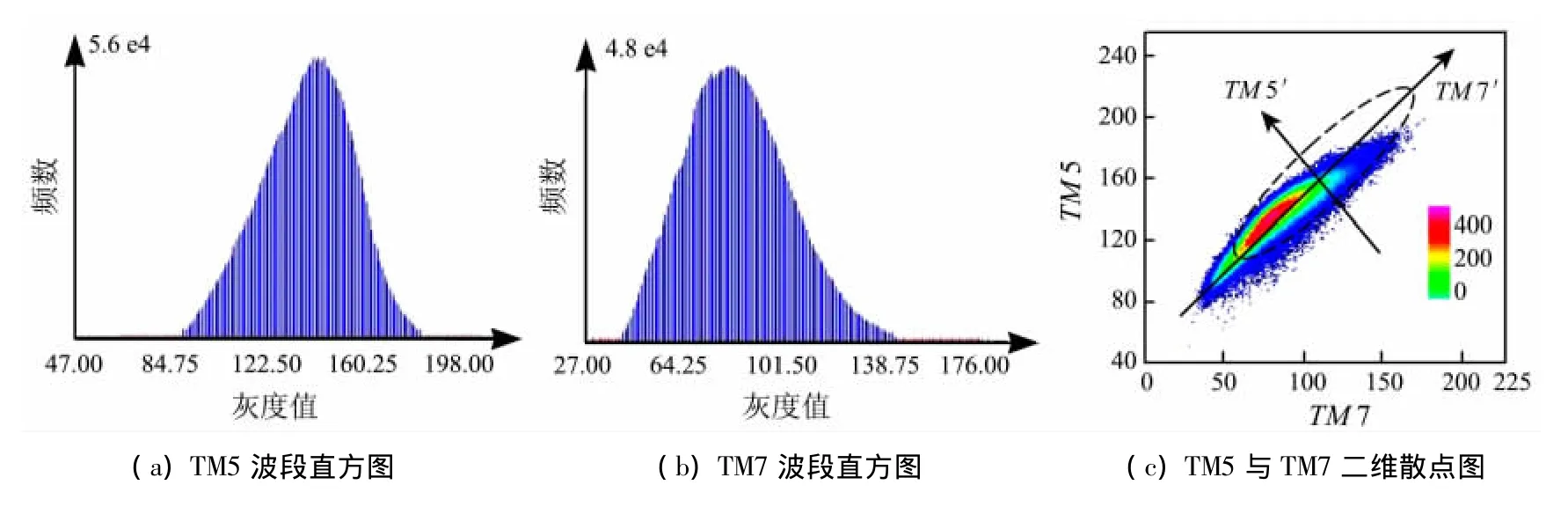
图1 青海省黄南州吉地地区TM图像数据直方图与二维散点图Fig.1 The histograms and two - dimensional scatter plots of TM image in Jidi area of Huangnan in Qinghai
实际上,经常见到的2个不同波段遥感数据的二维散点图会类似于图1(c)的近似椭圆形态,这种形态的二维散点图表明这2个波段的联合概率密度函数基本服从二元高斯分布。若设变量X1,X2遵从二元高斯分布(又称二元正态分布),则其概率密度分布[9]为
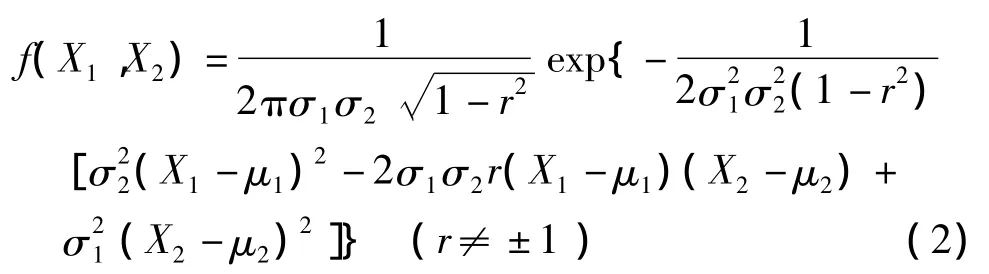
式中,μi与σi分别为变量Xi的均值与均方差(i=1,2);r是X1与X2的相关系数。
2.2 二维高斯分布椭圆形态的数学推导
对于二维概率密度函数,式(2)的二维高斯分布是否存在一个理论椭圆方程?下面采用数学方法加以推导求证。
令A为变量X1、X2的协方差矩阵,其形式为

则推导出式(2)最后的椭圆方程为
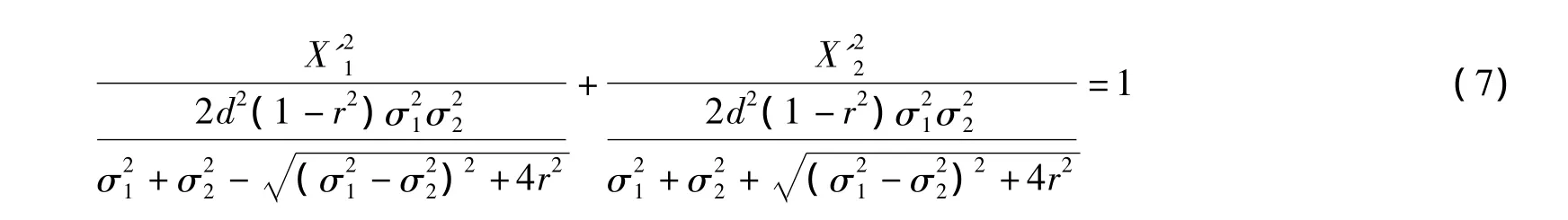
图1(c)给出了二维分布的椭圆形态及坐标轴由 X1、X2旋转至 X'1、X'2的示意图。
2.3 二维高斯分布椭圆几何参数特征
下面讨论式(7)椭圆方程的几何参数特性,即该椭圆长轴与短轴同X1、X2两个随机变量的方差与相关系数的关系。
若令 σ1=aσ2,为不失一般性,这里假设 σ1≥σ2,则有 a≥1,式(7)可变为
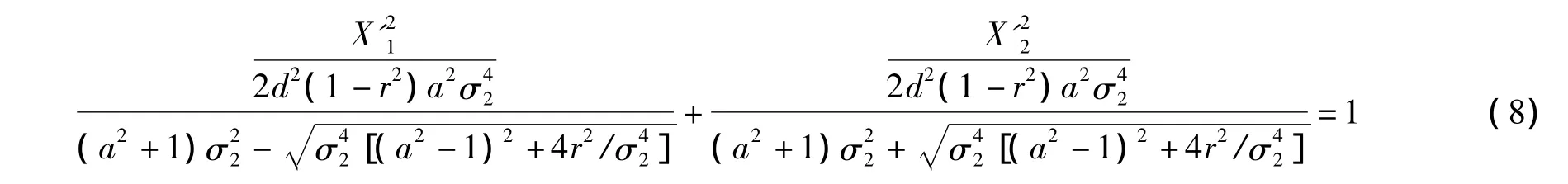
由于遥感图像数据的方差大多比较大(一般σ ≥10),所以项可看作近似于0,式(8)可简化为

由式(9)~(11)可得到如下结论:
(1)在两个随机变量均方差较大的情况下,其二维高斯分布所构成的椭圆体的长半轴、短半轴分别同两个随机变量的标准方差成正比(呈线性关系),并与两个变量的相关系数r成反比(呈非线性关系);
(2)当σ1=σ2=1时,椭圆的长半轴同两个变量的相关系数r成正比,短半轴则与相关系数r成反比;

3 不同直方图生成的二维散点图的结构特征与异常信息空间定位
由上述分析可知,遥感图像数据的均值、方差、偏度及峰度决定了直方图(一维概率密度分布)的分布形态与统计特征,而波段数据直方图的上述统计特性与波段之间的相关系数又确定了二维散点图(二维概率密度分布)的空间结构与统计特征。通过分析由不同分布类型的直方图组合生成的二维散点图的形态结构特征,能够确定异常信息在散点图上的大致位置。这里的异常信息主要指干扰地物与蚀变信息[2]。
根据前面的分析,遥感图像直方图的基本分布包括:高斯分布、亚高斯分布(多峰分布)、左偏超高斯分布和右偏超高斯分布,4种不同直方图分布的组合共有10种。下面对这10种直方图组合进行分析。
(1)高斯分布-高斯分布。在一幅图像中,存在2个都是高斯分布的波段很少,一般只有低空间分辨率的图像(如MODIS数据)才有可能常出现这种情况,其原因是由于像元混合光谱造成的。中高空间分辨率的图像出现这种情况比较少。① 若2个波段高度相关,这样的波段一般只含有背景信息,即2个波段图像越接近高斯分布,在其生成的二维散点图上越无法观测到明显的异常聚类结构,而且越接近高斯分布的数据,其二维散点图越细长(例如图1(c)是由稍有偏度的近高斯分布的图像生成的二维散点图);② 当2个波段出现负相关时,其图像也主要包含背景信息,但其背景“椭圆”主轴呈现负斜率。
(2)亚高斯分布-亚高斯分布。服从亚高斯分布(多峰分布)的波段图像(图2(a)、(b)),其信息量是最丰富的,由这种分布的2个波段生成的二维散点图也是最具结构信息的。① 较低相关(指r<9.80)的2个波段生成的二维散点图主要反映背景与大干扰的信息;② 高相关(指r≥9.80)的2个波段生成的二维散点图则能凸显异常信息(指蚀变信息与小干扰异常)。
不管反映何种类型的信息,其异常“聚类”通常会在二维散点图椭圆长轴方向的一侧或两侧的边界上(图2(c))。
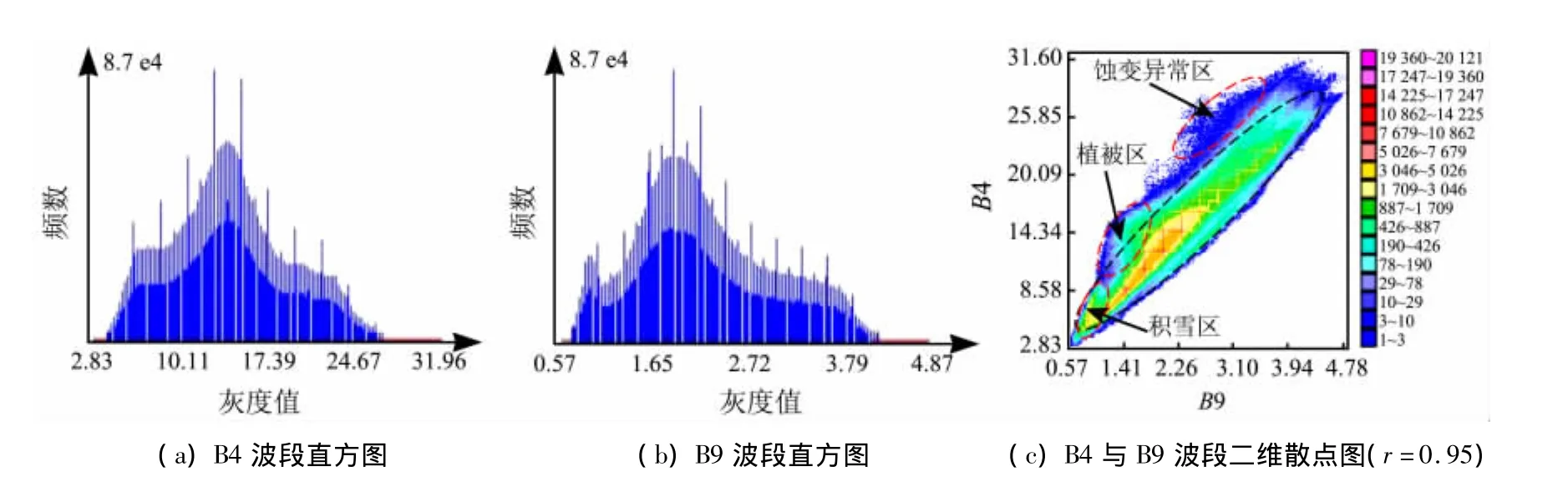
图2 柴达木北缘乌恰地区Aster图像B4、B9波段数据直方图与二维散点图Fig.2 The histogram s and two - dimensional scatter plots of the band B4 and B9 of Aster image in Wuqia area in the north of Qaidam
(3)左偏超高斯分布-左偏超高斯分布。这种类型分布的图像异常信息主要在高值区。① 当2个波段均为左偏分布且形态与宽窄相近时,即高相关(r≥0.95)的二维散点图,大多情况下其异常“聚类”会出现在二维散点图椭圆长轴方向的右端点上;②若2个波段均为左偏分布,但主峰包含有多峰时,具有较低相关(r<0.95)的二维散点图,其异常“聚类”会产生分裂,且它们分布在长轴方向端点的两侧;③若2个波段均为左偏分布,但宽窄相差悬殊时,属于低相关(r<0.90)的二维散点图,其异常“聚类”会产生“大头”现象;④ 若2个波段均为左偏分布并伴右侧小峰,而且形态与宽窄不相同的话,属于较低相关(r<0.95)的二维散点图,其异常“聚类”会明显分布在长轴方向椭圆的两侧;⑤若2个波段左偏且宽度相差较大时,其异常“聚类”会向偏度大的波段方向偏转。
(4)右偏超高斯分布-右偏超高斯分布。该类型分布同左偏超高斯分布-左偏超高斯分布的情况刚好相反,图像异常信息主要在低值区。①高相关(r≥0.95)的二维散点图,其异常信息主要集中在椭圆主轴方向的左端点上;② 低相关(r<0.95)的二维散点图,其异常信息不仅分布在椭圆方向的左端点上,而且还会出现在椭圆朝向左偏较大波段一侧的边界上;③当右偏形态还伴有右侧小峰时,大多情况下其异常“聚类”会出现在二维散点图椭圆长轴方向的两侧的边界上。
(5)高斯分布-亚高斯分布。暂时未见这种类型的例子。
(6)高斯分布-左偏超高斯分布。这种组合2个波段的相关性一般都较低,二维散点图的形态主要取决于左偏超高斯分布之直方图的左偏程度。它的背景中心位于低值端,异常信息分布在高值端且异常点群形态偏向于左偏的波段。这种情况的异常信息主要是由大干扰地物引起的。
(7)高斯分布-右偏超高斯分布。暂时未见这种类型的例子。
(8)亚高斯分布-左偏超高斯分布。这种组合类型必然是低相关的2个波段,其散点图的异常“聚类”是由大干扰信息造成的,异常“聚类”会偏向于左偏的波段。
(9)亚高斯分布-右偏超高斯分布。同亚高斯分布-左偏超高斯分布的情况一样,这种组合属于2个低相关的波段,其散点图的异常“聚类”主要是由大干扰信息造成的,异常“聚类”会偏向于左偏程度大的波段一侧。
(10)左偏超高斯分布-右偏超高斯分布。这样的组合其2个波段通常不会有很高的相关性,而且它们的偏度越大,其相关程度越低。这种情况的二维散点图主要包含的是背景或大干扰异常信息。①低相关波段组合的二维散点图,异常“聚类”偏向于左偏波段,但尾部向右偏波段的低值端延伸;②较高相关(r≥0.90)波段组合的二维散点图,异常“聚类”也偏向于左偏波段,但右偏波段的低值端的拖尾现象不明显。
4 应用实例
以青海省巴音山地区的TM图像为例,阐述遥感数据二维散点图的空间结构分析过程及其在蚀变信息提取中的应用。
图3给出了该地区TM图像的TM3和TM4两个波段的直方图及它们的二维散点图。TM3波段属于亚高斯分布(图3(a)),而TM4波段基本上可看作右偏超高斯分布(图3(b)),这2个波段属于“亚高斯分布-右偏超高斯分布”类型(第9种类型)。因此:①它们的相关性不会太高,这里TM3与TM4的相关系数r只有0.74,在遥感波段数据中是比较低的;②散点图的异常“聚类”主要是由大干扰信息造成的,此例的大干扰为植被信息;③异常“聚类”会偏向于左偏程度大的波段一侧。比较2个波段,TM4波段的左偏程度明显大于TM3波段。所以,这里的植被“聚类”,无论是暗区植被或是混合区植被点群,其长轴均偏向于TM4坐标轴一侧(图3(c))。
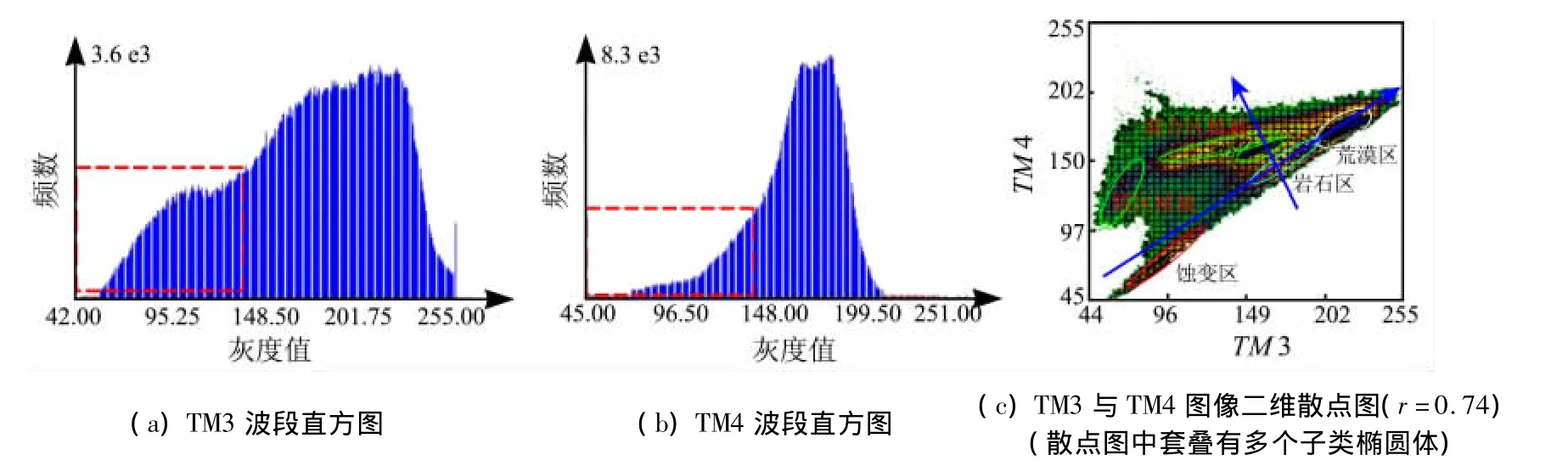
图3 巴音山地区TM3和TM4的直方图与二维散点图Fig.3 The histograms and two - dimensional scatter plots of TM 3 and TM 4 in Bayin mountain area
本例中2个波段的直方图形态差异很大,且均不是高斯分布,所以它们生成的二维散点图不是椭圆形态;但散点图中存在子类椭圆套叠结构特征,各主要地物子类的小椭圆清晰可见(在图3(c)中可见到的子类地物有荒漠区、岩石区、暗区植被、混合区植被等)。值得注意的是,根据2个波段直方图的异常信息区位置以及蚀变信息的物理意义与地质意义,在图3(c)的二维散点图上确定出蚀变信息区子椭圆(见图3(c)中的红色小椭圆);而且,蚀变信息区子椭圆同其他子类地物小椭圆的边界清晰,说明经二维散点图空间结构分析后,该地区蚀变信息的提取将变得比较容易。
图4为采用该地区TM3和TM4波段数据、用笔者自己研发的二维彩色相关编码技术提取得到的遥感蚀变异常信息图像。
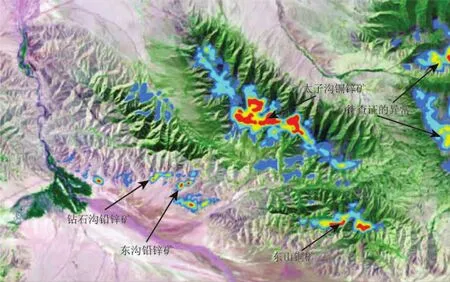
图4 巴音山地区遥感蚀变异常信息图像Fig.4 Remote sensing alteration information image in Bayin mountain area
图4表明,该地区的几个已知矿床都在蚀变异常区中;而且,除了高海拔的几个蚀变异常区暂未查证外,其他异常区经野外查证均见到矿化蚀变现象,正在做进一步的地质勘查工作。
5 结论
(1)遥感图像信号属于随机信号,一维与二维概率密度函数分别是单波段和两波段的随机模型。而单波段数据直方图与两波段二维散点图又分别是一维和二维概率密度函数的基本估计。
(2)本文讨论了遥感数据直方图的概率密度分类、二维散点图的基本形态与特征,同时从数学上推导出二元高斯分布的椭圆理论方程,并由此分析了二维椭圆的参数同2个波段数据的方差与相关系数等统计参数的重要关系。
(3)在上述工作的基础上,根据直方图的概率密度类型,系统总结了不同类型直方图组合生成的二维散点图的基本特征、空间结构形态与异常“聚类”信息的空间定位等。
(4)通过实例说明了遥感数据空间结构分析的重要性与实用性。
[1]张远飞,杨自安,朱谷昌,等.遥感图像蚀变信息检测中的光谱数据空间结构分析[J].遥感信息,2009(1):3-9.
[2]张远飞,吴德文,朱谷昌,等.遥感蚀变信息检测中背景与干扰问题研究[J].国土资源遥感,2008(2):22-26.
[3]李 红,朱谷昌,张远飞,等.矿化蚀变区典型地物光谱特征分析——以内蒙古突泉县—扎鲁特旗成矿带为例[J].国土资源遥感,2010(1):89-95.
[4]张远飞,吴德文,张艮中,等.高光谱数据的波段序结构分析与应用研究[J].国土资源遥感,2010(1):30-38.
[5]李智勇,郁文贤,匡纲要,等.基于高维几何特征的高光谱异常检测算法研究[J].遥感技术与应用,2003,18(6):379 -383.
[6]Hyvrinen A,Karhunen J,Oja E,等,著.周宗潭,董国华,徐 昕,等,译.独立成分分析[M].北京:电子工业出版社,2007.
[7]马建仓,牛奕龙,陈海洋,等.盲信号处理[M].北京:国防工业出版社,2006.
[8]Kenneth R C.著.朱志刚,林学訚,石定机,等,译.数字图像处理[M].北京:电子工业出版社,2002.
[9]何晓群.现代统计分析方法与应用[M].北京:中国人民大学出版社,2007.
(责任编辑:刘心季)
A Study of Spatial Structure Analysis and Alteration Information Extraction Based on Random Models of Remote Sensing Data
ZHANG Yuan - fei1,2,YUAN Ji- ming1,ZHU Gu - chang1,WU De - wen1,LIHong1,3
(1.China Non -ferrous Metals Resource Geological Survey,Beijing 100012,China;2.Guilin Research Institute of Geology for Mineral Resources,Guilin 541004,China;3.Centre South University,Changsha 408309,China)
Remote sensing image signals are random signals whose band data histograms and two-dimensional scatter plots are respectively the basic estimates of one-dimensional probability density function and two dimensional probability density function of the random model.In this paper,the basic types and patterns of one -dimensional probability density and the geometric parameter characteristics of Gaussian distribution ellipses are discussed based on the random models of remote sensing data.Then,problems such as the spatial geometric structure characteristics of the two-dimensional scatter plots generated by different histograms and the positioning in abnormal information space are analyzed.At last,the importance and practicability of the spatial structure analysis of remote Sensing data in alteration information extraction are demonstrated by a case study.
Remote sensing data;Random models;Spatial structure analysis;Alteration information extraction
张远飞(1958-),教授级高级工程师,主要从事遥感技术方法及地质应用研究。
TP 75
A
1001-070X(2010)04-0034-06
2010-01-21;
2010-03-18
国家高科技研究发展计划(863)资助项目(编号:2006AA06Z112)和国家科技支撑项目(编号:2006BABA06)共同资助。
