沙堆模型的原理及其在电力系统中的应用

马士英，马新惠，周任军，张世海

（1.长沙理工大学电气与信息工程学院，长沙市，410014；2.贵州电力试验研究院，贵阳市，550002）

0 引言

近几年，国内外电力系统发生了多次大停电事故。特别是2003年8月14日的美国东北部、中西部和加拿大东部联合电网发生的大停电，震惊了世界[1-4]。这些事故，引起了国内外许多的学者对大停电的思索和研究，他们期望能找出一种简单易行的方法来研究电力系统大停电，从而可以进一步对电网大停电的发生时间和规模进行预测。

众所周知，电力系统正常运行过程中电力元件均要发热[5]，若是电力系统运行过程中的温度超过系统正常运行时的温度，则可能是系统设备中某个或某些元件发生了故障，从而使电力系统过载或过负荷，造成电力系统停运，甚至是电网的崩溃。文献[6]表明电力系统大停电具有自组织临界特性。类比电力系统过载或过负荷也可能具有基于自组织临界理论中的协同学原理所揭示的规律。同时文献[6]阐述了沙堆模型可以形象地说明基于自组织临界理论中的协同学原理。电力系统过载或过负荷也可以利用沙堆模型形象地进行模拟仿真，对电力系统过载或过负荷现象进行简单易懂地定性或理论方面的研究，从而可以提前判断电力系统过载或过负荷现象，降低电力系统故障发生的机率，保障电力系统正常运行。

沙堆模型可以形象化地说明许多原理，并且能够简单地模拟仿真这些原理，因而，在国内外沙堆模型已经被应用在许多行业，近年来更是被越来越多地应用到电力行业中，用来模拟仿真电力系统中的故障分布特性和严重程度。例如沙堆模型在文献[6]，文献[7]和文献[8]中的应用，等等。而且，根据沙堆模型的目前发展趋势可以预测，在不久的将来，沙堆模型也可以应用于模拟仿真电力系统过载或过负荷的分析研究上。

沙堆模型能够描述电网的一些规律，在电力系统中具有潜在的应用背景。鉴于沙堆模型在电网中的潜在应用，本文主要依据沙堆模型的定义，对沙堆模型进行仿真编程，为今后进一步利用沙堆模型，研究其在电力系统中的应用打下基础。

1 原理介绍

1.1 自组织理论

自组织理论是20世纪60年代末期开始建立并发展起来的一种系统理论。自组织理论认为：客观实际存在的系统都是开放系统，即系统与外界环境存在着物质交换、能量和信息交换[6-8]。它的主要研究对象是复杂自组织系统（生命系统、社会系统）的形成和发展机制问题，即在一定条件下，系统是如何自动地由无序走向有序，由低级有序走向高级有序的。自组织现象是指把一个系统内部从无序变为有序，使其大量分子按一定规律运动的现象。这种现象在自然界中是大量存在的，理论研究较多的典型实例有：贝纳德（Baynard）流体的对流花纹，贝洛索夫一扎鲍廷斯基（Belousov-Zhabotinsky）化学振荡花纹与化学波，激光器中的自激振荡等。协同学（Synergetics）是自组织理论之一。

1.2 协同学原理

协同学亦称为协同论或协和学，是德国教授哈肯（Hermenn Haken）在1976年创立的。协同学是一门研究远离平衡态的系统如何通过各子系统之间的自我组织产生时间、空间或功能结构的科学，其主要目的是在现实世界中探求各种不同现象的普遍规律[7]。协同学研究协同系统在外参量的驱动下和在子系统之间的相互作用下，以自组织的方式在宏观尺度上形成空间、时间或功能有序结构的条件、特点及其演化规律。协同学的主要内容就是用演化方程来研究协同系统的各种非平衡定态和不稳定性（又称非平衡相变）。协同学认为：世界的统一性不仅在于它们的微观结构的单一性，而且在宏观结构的形成中也遵从某些普遍规律[8]。同时哈肯在协同学中描述了临界点附近的行为，阐述了慢变量支配原则和序参量概念，认为事物的演化受序参量的控制，演化的最终结构和有序程度决定于序参量。

1.3 沙堆模型

沙堆模型是自组织临界理论中的协同学原理的形象化表述[6，8]，因而沙堆模型原理同样遵循协同学原理。在沙堆模型中，设置漏斗功能，使每次只流下1粒沙粒。沙粒从漏斗中不断流到平板上，随着沙粒数的增多，逐渐在平板上形成了一种略呈圆锥形状的沙堆，沙堆堆底不是完全对称的，而且堆体表面有些凸凹不均，坡角也不是一致的。在沙粒流下的初始阶段，沙粒数量较少，各处坡角也比较小，这时即使坡角大的某一处发生滑坡，产生沙崩，对其周围的沙粒产生了影响，增大了某些地方的坡角，但增大后的坡角一般与临界安定角相差较远，此时还不至于引起新的沙崩。随着流下沙粒数量的增加，沙堆各处的坡角逐渐增大，平均坡角开始慢慢地向临界安定角逼近，若这时发生沙堆滑坡，产生沙崩，情况就和上述状况不同了。此时，某一处发生滑坡产生小沙崩，就会对周围的沙粒产生影响，引发规模不同的沙崩。这种情况表明沙堆模型已经开始接近其自组织临界状态，即此时的沙堆模型很大程度上可以形象地表示协同学原理。

2 数学建模

应用于模拟仿真的沙堆模型普遍熟知的是奥斯陆模型（Olso-model），而且这类模型具有随机更新规则，它的临界坡度通过崩塌动态调整[9]。在模型的最初的一维空间中，沙粒流入1个具有若干个位点的平板上。当这个沙堆的局部边坡在这个位点和它的邻近的位点之间被赋予不同的高度，超过1个类似的局部极限时，沙粒通过下滑1个沙粒倾覆到邻近的位点（从位点i到位点i+1）重新分布。这种做法是由1粒沙通过降低位置i的高度并且通过这个沙粒来增加位置i+1的高度，而且，在这样的倾覆事件中局部极限被重新选择。这个程序被反复执行，直到所有的位点都达到稳定状态，在这个稳定状态点，1个新的沙粒流入到它的左侧。由于这种更新规则的随机化，在模型中平均临界坡度实际上自组织到1个固定的值。这个模型根据局部极限可以很容易地用公式表示成zi=hi-hi+1[9]的形式。如果是这样的话，其规则如下所示：

当 zi＞zc[9]时，

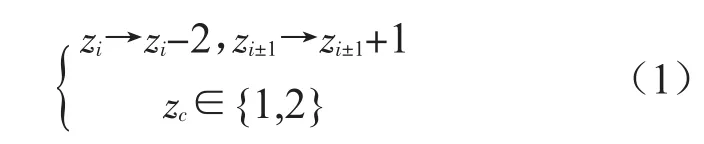
在这个表达公式中，模型的最初的沙堆性质不是直接地显而易见的，然而，将其延伸到较高维数就会变得简单易懂。这种模型的较高维空间也可以有效地应用在沙堆上，但在以下的叙述中，附加的维数将要考虑到空气的特性，这种倾覆规则最简单可能延伸（方程（1））到二维，同时包括下列的更新规则[9]：

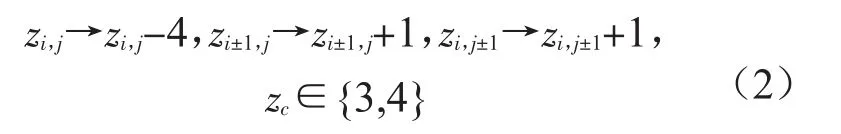
适合于这种二维空间的更新发生在x轴的x=0时，在各自的崩塌后，它的值被增加1个（例如，z0，j→z0，j+1[9]）。在y轴，周期的边界条件是设定的，而在x轴的边界条件是公开的。

3 程序实现

设定沙粒流入具有n×n个位点的板上，沙粒数量为l，规定每个位点的沙粒数不能超过4个，若有1个位点的沙粒数超过了4个，则遵循就近原则，沙粒数超过4个的位点将选择和这个位点最近的位点，将多余的1个沙粒倾覆到它最近的位点，这个程序被反复执行，直到所有的位点都满足沙粒数不超过4个，达到稳定状态。沙堆模型的程序流程图如图1所示。

图1 沙堆模型的程序流程图Fig.1 Program flow chart of sand pile model

根据上面的程序流程图可以很容易地编写出沙堆模型的程序，其部分源程序如下所示：

function sp=sandpile（n）

temp=0;

clc

k=-1;

l=0;

xtemp=linspace（k，k，100）;

ytemp=linspace（k，k，100）;

num=n;

%Numbers of grid

Sarray=zeros（num）;

while（l＜500）

xgrid=fix（rand*（num+0））+1;

ygrid=fix（rand*（num+0））+1;

Sarray（xgrid，ygrid）=Sarray（xgrid，ygrid）+1;

if Sarray（xgrid，ygrid）＞4

temp=1;

xtemp（1）=xgrid;

ytemp（1）=ygrid;

while（temp＞0）

xgrid=xtemp（1）

ygrid=ytemp（1）

if Sarray（xgrid，ygrid）＞4

Sarray=Saydear（num，xgrid，ygrid，Sarray）

[xtemp，ytemp，temp]=axidear（xgrid，ygrid，xtemp，ytemp，Sarray，temp）;

end

[xtemp，ytemp]=arrary（xtemp，ytemp，k）;

temp=temp-1;

end

end

l=l+1;

Sarray;

End

…………………………

根据编写的沙堆模型的程序，可以方便地计算沙堆模型。例如，设定板子上的位点数n=10，沙子的沙粒数量为500粒。执行程序后，可以很容易得到此种情况下沙粒的分布特性，其分布特性简单易懂地表明了沙堆模型具有基于自组织临界理论的协同学原理所揭示的规律。给定其他位点数和沙粒数，该沙堆模型同样具有一致的模拟结果。所以说沙堆模型可以很好地形象地说明协同学原理。

4 结果讨论

根据给定的沙堆模型的计算算例，总结出沙粒的分布特性是符合协同学原理的。其相似的分布特征可以在电力系统大停电数据中发现。类比在电力系统过载或过负荷的数据中，具有与沙堆模型相似的分布特征，则沙堆模型所揭示的规律也能够较好地反映电网的过载或过负荷过程，由此可以根据实际电网过载或过负荷前的有限数据预测电网过载或过负荷的发生时间，为防止由于电力系统过载或过负荷引起的故障提供较充足的处理时间，从而可以减少故障发生的概率。

应当指出，沙堆模型能够描述电网的一些规律，而本文所做的工作只是初步的，给出了沙堆模型的程序，演算了程序的执行过程，分析了其分布特性，说明了沙堆模型可以形象地阐明协同学原理的自组织过程，为其在电力系统中的应用提供理论基础。但并没有过多地和电力系统进行联系，沙堆模型在电网大停电研究中的应用也是结合国内外近几年的发展进行定性的阐述，其在电力系统过载或过负荷上的应用，只是提出了一种应用可能性，因此沙堆模型在电力系统中的实用性需要今后做进一步的深入研究。

[1]甘德强，胡江溢，韩祯祥.2003年国际若干停电事故思考[J].电力系统自动化，2004，28（3）：1-5.

[2]唐葆生.伦敦地区大停电及其教训[J].电网技术，2003，27（11）：l-5.

[3]赵希正.强化电网安全保障可靠供电：美加“8·14”停电事件给我们的启示[J].电网技术，2003，27（10）：1-7.

[4]何大愚.一年以后对美加”8·14”大停电事故的反斟[J].电网技术，2004，28（21）：1-5.

[5]王晓林.电力设备故障红外诊断技术及其应用[J].甘肃电力技术，2005（1）：9-15.

[6]曹一家，江全元，丁理杰.电力系统大停电的自组织临界现象[J].电网技术，2005，29（15）：1-5.

[7]曹一家，丁理杰，江全元，等.基于协同学原理的电力系统大停电预测模型[J].中国电机工程学报，2005，25（18）：13-19.

[8]柳 近，张世杰，李来福，等.类比沙堆模型的电网危害性展示模型[J].继电器.2007，35（增刊）：354-358.

[9]Aegerter Cm.A sandpile midel for the distribution of rainfall?[J].PhysicaA，2003（319）：1-10.