小麦面粉指标关系中的 Fuzzy非线性回归问题

史本广,许小艳,程 涛,匡国光

(河南工业大学理学院,河南郑州 450052)

小麦面粉指标关系中的 Fuzzy非线性回归问题

史本广,许小艳,程 涛,匡国光

(河南工业大学理学院,河南郑州 450052)

小麦面粉指标关系大都呈现一定的模糊性.利用 Fuzzy结构元理论对小麦面粉指标中的模糊关系进行了分析,给出了一种处理模糊非线性关系的 Fuzzy非线性回归模型,实例表明模型适用,既为处理模糊关系提供了一种新方法,也为小麦面粉的综合研究提供参考.

面粉指标;模糊回归;模糊数;参数估计

0 前言

小麦面粉的质量直接涉及国计民生,因此对小麦面粉的研究一直是有关部门所关心的问题.为便于小麦面粉的综合利用,应首先对小麦面粉各指标间关系进行分析,找出它们之间的内在联系.但小麦面粉各指标间的数据或结论的来源带有不确定性,有的还带有人为因素,换句话说带有模糊性,有学者对小麦面粉各指标间的关系应用模糊数学的观点、方法去处理[1,2,6],给出了各指标间关系的 Fuzzy线性回归模型[3],但误差过大,也就是模糊度过大,为此,笔者利用 Fuzzy结构元理论对小麦面粉指标关系进行讨论,得出关于小麦面粉指标间的模糊非线性回归关系.这不但扩大了模糊数学的应用领域,而且对于小麦面粉各指标间的关系提出了一种新的、可行的应用模型,在小麦面粉的综合研究方面具有一定的参考价值.

1 预备知识

定义 1[4]设 E是实数集 R上的 Fuzzy集,隶属函数记为 E(x),x∈R.如果 E(x)满足:

(1)E(0)=1,E(1+0)=E(-1-0)=0;

(2)E(x)在区间[-1,0)上是单调右连续函数,在区间(0,1]上是单降左连续函数;

(3)当 -∞＜x＜-1或1＜x＜+∞时,E(x) =0.

则称模糊集 E是 R上的 Fuzzy结构元.

定义 2[4]若 Fuzzy结构元的隶属函数在区间[-1,1]上有 E(x)＞0,且在 (-1,0)内是连续严格单增函数,在区间 (0,1]上是连续严格单降函数,则称 E是正则的 Fuzzy结构元.

定理 1[5]设θ是有限模糊数,则存在一个模糊结构元 E和有限实数 a和 c,使得θ=a+cE (c＞0).θ的隶属函数为:μ(θ)=E[(x-a)/c].

定义 3[5]设 g(x,y)=f(x)+w(x)y.其中f(x)和 w(x)在 X上有界、且 w(x)非负.易知g(x,y)是关于 y在 [-1,1]上的单调有界函数,则(x)=f(x)+w(x)E是 X上的一个模糊值函数,称为由模糊结构元 E线性生成的模糊值函数.的隶属函数为

2 模糊回归模型

设 g为 Rm→R的函数

式中:x1、x2、…、xm为自变量,θ1、θ2、…、θn为实值参数,对固定的 x1、x2、…、xm视θ1、θ2、…、θn为实参数,并假设函数 g关于自变量及实值参数是连续可微的,则函数 g可视为 Rn→R的函数,对此应用 Zadeh多元函数扩展原理有

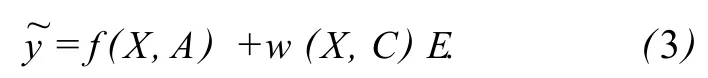
显然 (3)式可作为研究 X与 y之间的模糊回归模型,当 f(X,A)为 X的非线性函数时,也称(3)为非线性回归模型,其中 A,C可作为待估计的参数.的隶属函数为

若对 (1)式有观测值 Xi=(x1i,x2i,…,xmi),对应的 y可能有一组值 yi=(yi1,yi2,…,yis(i)),则对应于(3)式有

式中:i=1,2,…,k.取 yi的隶属函数为如下三角结构元:

则有 D=(yi-f(Xi,A))/w(Xi,C).

显然 (3)式作为回归模型,应考虑 w(Xi,C)＞0且越小越好,同时要求 yi属于程度越大越好,一般若控制在 h∈(0,1]的水平下,即

从而可得如下的规划问题:

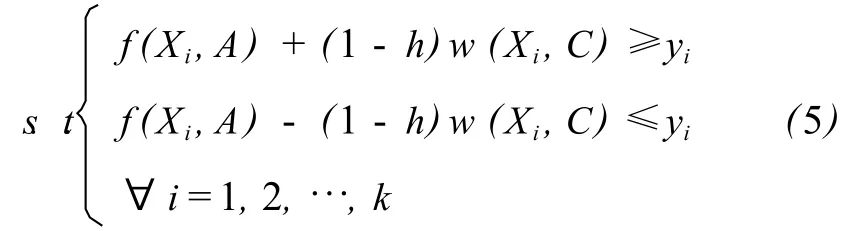
求出参数A,C,即得实自变量 X与模糊变量y之间的模糊回归模型(2).

3 小麦面粉指标关系中的 Fuzzy非线性回归问题

3.1 小麦面粉指标

小麦粉的粉质曲线特性及小麦麸皮戊聚糖组分对面团粉质特性指标见表 1[7]及表 2[7].

表 2 小麦麸皮戊聚糖组分对面团粉质特性指标的影响

表 1和表 2均为人为的观察值,由于人的心理测量因素的影响,这些观察值之间存在误差,所以这些观察值应该都是模糊的,因此用模糊回归模型解决小麦面粉各指标之间关系会比经典回归更为有效.

3.2 小麦面粉指标中的模糊回归

利用表 2中的数据,以添加比例 x1和弱化度x2为相关变量,以稳定时间 y为因变量,建立Fuzzy回归模型.由 (3)式,根据经典数学的方法用Mathematica可拟合出函数

若令 x3=,则 f(X,A) =14.8156+ 2.21487x1-0.12987x2-1.29818x3,从而可取w(X,C) =c0+c1|x1|+c2|x2|+c3|x3|.由(5)式即得添加比例 x1和弱化度 x2与稳定时间 y为因变量的值满足如下的规划模型

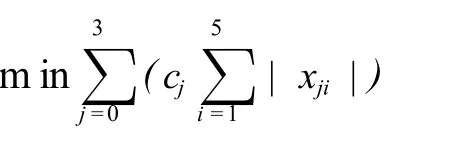
根据表 2所给数据,运用 EXCEL可求得

从而可得添加比例x1和弱化度x2为相关变量,以稳定时间 y为因变量的非线性模糊回归模型为

则当 x1=1.5,x2=60时,有=7.4248+ 0.2838E.而表 2中的实际观察值为 7.5,恰好落在区间 [7.4248,7.7086]内,且结果优于文献[3],这说明模糊非线性回归模型更能反映实际,并表明模糊非线性回归模型应用于小麦面粉指标间关系的研究是可行的.

4 结论

(1)作者利用 Fuzzy结构元理论讨论了模糊回归模型的模糊参数的估计,并把 Fuzzy结构元理论应用到小麦面粉指标的研究中,得出了小麦面粉指标间的模糊关系,其结果更能反映实际.

(2)首次把模糊非线性回归模型应用到小麦面粉指标间关系的研究,既开拓了模糊数学的应用领域,也为模糊数学应用于粮油食品提供了一种方法.

(3)通过计算结果的比较,说明模糊非线性回归模型更能反映实际,并表明模糊非线性回归模型应用于小麦面粉指标间关系的研究是可行的,对小麦面粉的综合研究具有一定的参考价值.

[1] 曹炳元,朱章遐.含三角模糊参数的线性回归模型的新解法[J].汕头大学学报:自然科学版,2004,19(4):1-7.

[2] 谢季坚,刘承平.模糊数学方法及其应用[M].第2版.武汉:华中科技大学出版社, 2000:259-286.

[3] 史本广,林恒强,史磊.小麦面粉指标关系中的 Fuzzy回归分析[J].河南工业大学学报:自然科学版,2009,30(4):81-83.

[4] 曾繁慧.模糊线性回归分析的结构元理轮[J].科学技术与工程,2005,5(10): 635-639.

[5] 赵宏霞,杨皎平,郭嗣琮.基于模糊结构元方法的模糊线性回归模型[J].辽宁工程技术大学学报,2004,23(3):418-420.

[6] 肖辞源.工程模糊系统[M].北京:科学技术出版社,2004:259-263.

[7] 王金水,张丽萍,卞科,等.利用 HMW麦谷蛋白亚基组成建立小麦品质鉴评程序[J].郑州工程学院学报,2003,24(4):1-4.

FUZZY NONL INEAR REGRESSION ON THE INDEX RELATION OFWHEAT FLOUR

SH IBen-guang,XU Xiao-yan,CHENG Tao,KUANG Guo-guang
(School of Science,Hennan University of Technology,Zhengzhou450052,China)

The relationship among the indexes of wheat flourmostly shows fuzziness.The article analyzed the fuzzy relationship among the indexes of the wheat flour based on the Fuzzy structured element theory,and put for ward a Fuzzy nonlinear regression model for processing the fuzzy nonlinear relationship.The result shows that the model is feasible.Therefore,the article provides a novelmethod for processing the fuzzy relationship aswell as the references for comprehensive study ofwheat flour.

wheat flour index;fuzzy regression;Fuzzy number;parameter estimation

TS210

B

1673-2383(2010)03-0063-03

2010-04-12

河南省自然科学基金 (072300410100);河南工业大学自然科学基金(07XJC027)

史本广(1954-),男,河南商丘人,教授,主要从事数学教学及不确定性数学的研究.