基于ARIMA 模型的我国自然灾害救助支出研究(1978—2007)

赵黎明，王 忠

(天津大学管理学院，天津 300072)

基于ARIMA 模型的我国自然灾害救助支出研究(1978—2007)

赵黎明，王 忠

(天津大学管理学院，天津 300072)

对1978—2007年中国自然灾害救助支出数据进行了时间序列分析。分析表明，ARIMA(0，0，3)模型适合我国灾害救助支出建模。通过建模，结合求济人数与受灾人口之比、求助支出与受灾损失之比的统计数据，对我国自然灾害求助支出做了结构分析，并提出了相关改进建议。最后，利用所建模型进行了短期预测。

自然灾害;救助支出;ARIMA模型

一、引 言

我国是世界上自然灾害的多发国家之一，灾害爆发频率高，危害范围广，且具有交替性和群发性的特点。因此，自然灾害救助成为我国政府一项重要的职能，成为财政支出的重要组成部分。近年来，由于自然灾害造成的经济损失巨大，尤其是2008年的冰灾和汶川地震，使得灾害救助支出呈明显上升趋势。因此，对灾害救助支出的研究也逐渐升温。目前，对自然灾害救助支出的研究主要集中于以下两方面:1)自然灾害救助的渠道、方式，如孙婧［1］所做的研究;2)自然灾害救助资金的管理和配置，如祁毓［2］、郭显光［3-4］、赵卫亚［5］所做的研究。现有的这些文献大多属于理论研究。而对于我国自然灾害救助支出进行实证分析的文献相对缺乏。因此，本文将对1978—2007年我国自然灾害救助支出的数据进行时间序列分析，构建ARIMA模型;通过模型研究我国自然灾害救助支出的动态结构特性，再进行短期预测;最后提出相关改进建议，希冀为政府灾害救助提供借鉴。

二、数据及方法

1．数据来源及处理

根据我国现行灾害救助投入体制，财政对自然灾害的救助支出分为两部分:一是专项资金，设在“抚恤和福利支出”中的“救灾支出”项目下;二是通过抚恤支出、农业支出、科技支出、社会保障补助支出以及政策性补贴支出的一部分进行救助。此外，在遇到紧急特殊的自然灾害时，还可以通过中央和地方专项储备基金进行补助。这些救助共同构成了我国财政的自然灾害救济费，由民政部门负责管理。因此，本文数据来自于历年《民政事业发展统计公报》。由于统计公报中的自然灾害救济费是名义数据，没有考虑物价水平的变化，以此建模不能反映真实的经济意义。因此，模型中数据是消除价格水平后的真实数据。具体处理方法为:以1978年为基期，以各年的数值除以当年的物价指数。此外，为了消除可能存在的异方差，本文以对数建模，即对各真实数据取其自然对数建立模型。具体的数据见图1，NDR(natural disaster relief)表示真实的自然灾害救济费，对应右边刻度，LR表示取自然对数后的真实自然灾害救济费，对应左边刻度。由图1中NDR折线可见，历年的真实自然灾害救济费波动较大，整体有上升趋势。

2．研究方法

ARIMA模型是Box和Jenkins［6］提出的以随机理论为基础的时间序列分析方法，适用于各种领域的时间序列分析。时间序列模型不同于传统计量经济模型的两个特点是:1)建模方法不以经济理论为依据，而是依据变量自身的变化规律，利用外推机制描述时间序列的变化;2)明确考虑时间序列的非平稳性。如果时间序列非平稳，建立模型之前应先通过差分把它变换成平稳的时间序列，再进行建模。作为应用最广泛的时间序列分析方法之一，ARIMA模型能揭示相应系统的动态结构及发展变化规律，还可以用于预测［7］。

ARIMA建模过程分为四个步骤［8］:1)对原序列进行平稳性检验，若为平稳序列则转2)，因差分阶数d=0，此时构建的为ARMA模型，若为非平稳序列，通过差分变换变为平稳性序列，确定差分阶数d，再转2);2)计算自相关系数和偏自相关系数，绘制相关图，确定ARIMA模型的阶数p和q;3)估计ARIMA(p，d，q)模型的参数，并检验其显著性以及模型本身的合理性;4)检验模型拟合的准确性。本文建模过程借助Eivews软件完成。

图1 真实自然灾害救济费及其对数图

三、建模及检验

1．平稳性检验

建模前首先需要对数据进行平稳性检验。根据图1可知，LR序列具有趋势项和截距项。采用常用的Augmented Dickey-Fuller检验，对原序列进行检验，ADF 检验统计量为-4．993 890，其概率为 0．002 0。可见，LR序列在0．01显著性水平下为平稳序列。因此，可以直接在此序列上构建ARMA模型。

2．模型识别与定阶

由图1可以确定，本文将构建具有截距项和趋势项的ARMA模型。由自相关和偏自相关系数表1的拖尾性和截尾性，很难准确地确定ARMA(p，q)模型中p和q的阶数。然而，根据图2的特点，可以确定:p小于等于2阶，q小于等于4阶。因此，可以对p={0，1，2}和 q={0，1，2，3，4}进行排列组合，再对各种阶数组合的模型依次进行检验。

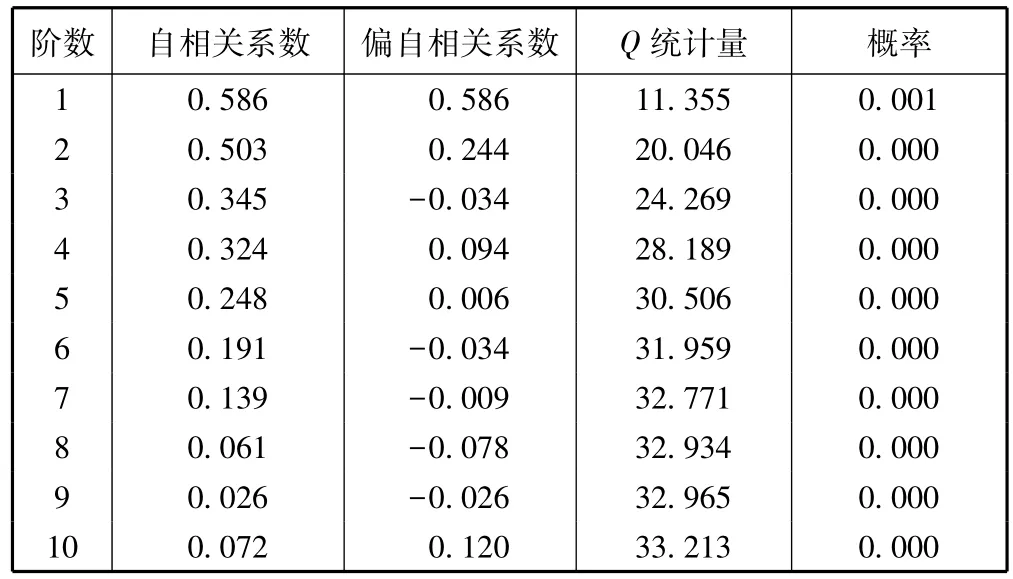
表1 自相关与偏自相关系数

3．模型检验

建立的模型是否成立应该从三个方面检查:1)模型参数估计量必须通过t检验;2)模型的全部特征根(包括自回归、移动平均两部分)的倒数都必须在单位圆以内(即模型具有平稳性和可逆性);3)模型的残差序列必须通过Q检验。同时也要尽量做到模型结构应当尽量简练、参数稳定性要好、预测精度要高［9］。经过多次比较，通过检验的为 ARMA(0，3)模型。因自回归阶数p=0，也即MA(3)模型。具体估计结果及t统计量和特征根的倒数见图3，Q统计量见表3。由表2和表3可见，t检验、特征根以及Q检验均符合要求。因此，MA(3)模型是成立的。

为测试模型预测精度，首先对1978—2007年数据分别进行静态和动态拟合，两拟合效果都很好。然后采用Chow Forecast Tests对模型进行稳定性检验，以1978—2004年数据建立 MA(3)模型，动态预测2005—2007的LR值，与真实值比较，预测精度很高，且估计参数与表2的无显著性差异。这说明其稳定性很好，因此确定构建MA(3)模型。

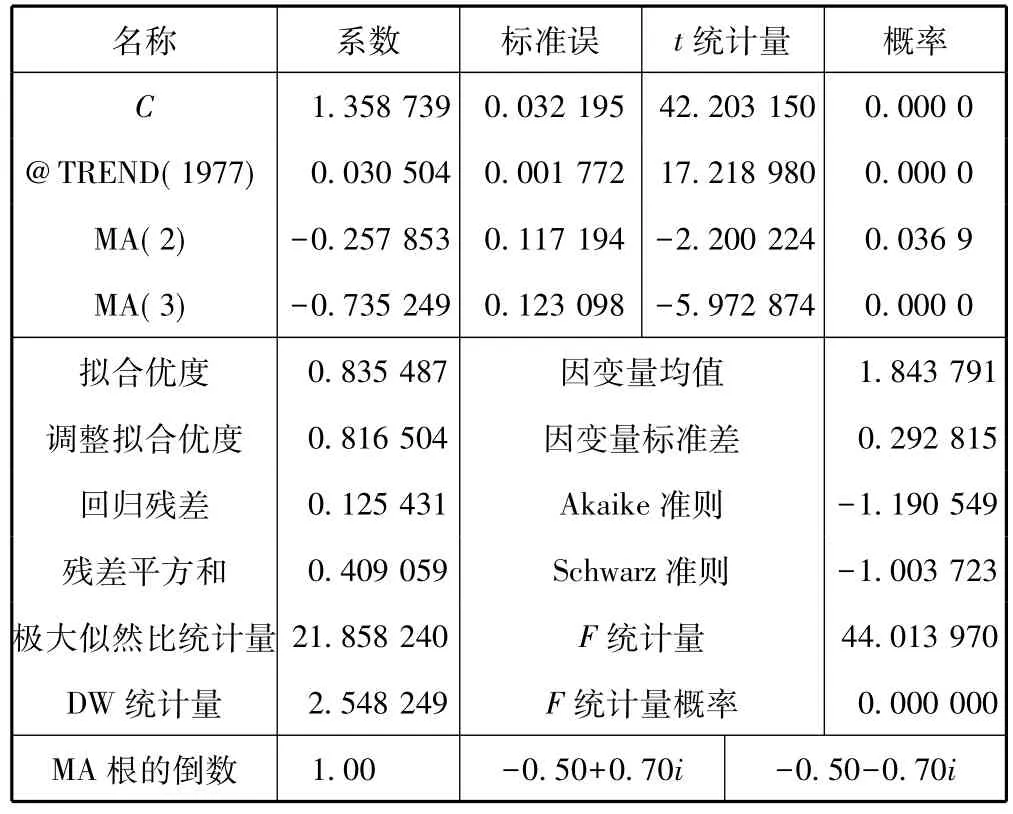
表2 模型估计参数

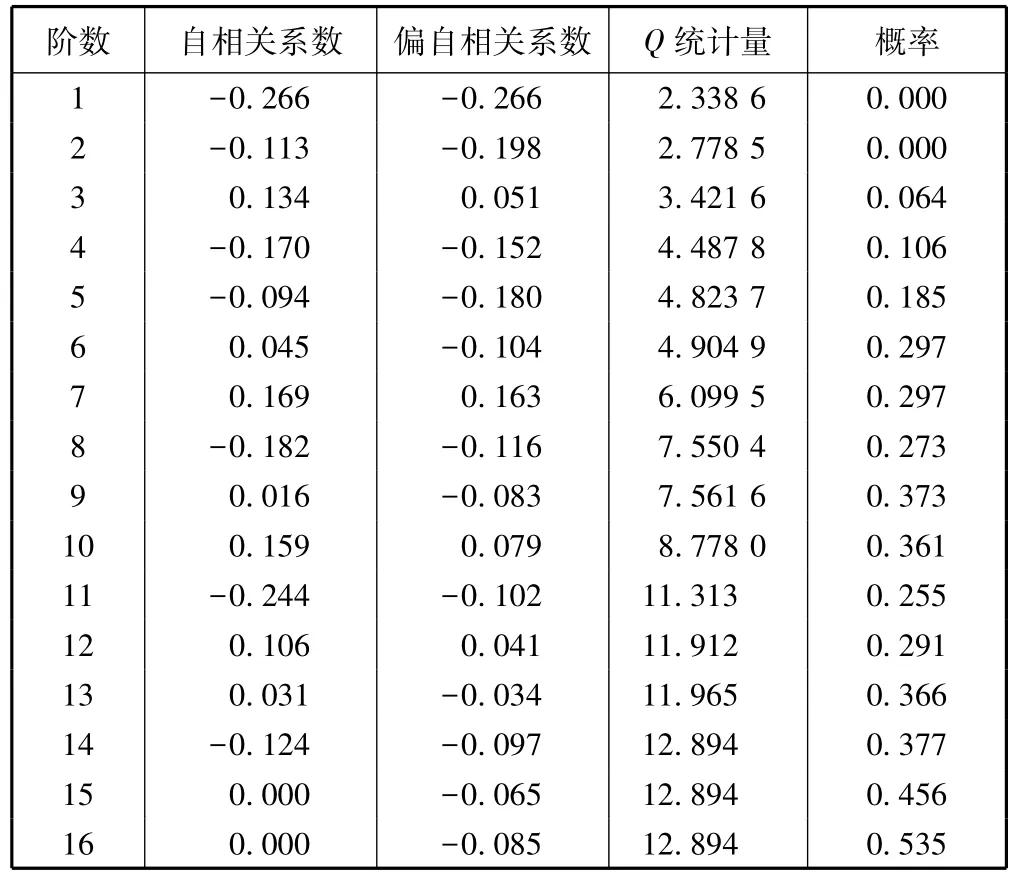
表3 残差Q检验

四、结构分析

合理的模型必须具有现实的经济意义。时间序列模型能很好地反映出系统的内在规律和动态结构，常常被用来进行结构分析。本文建立的模型具体如下。

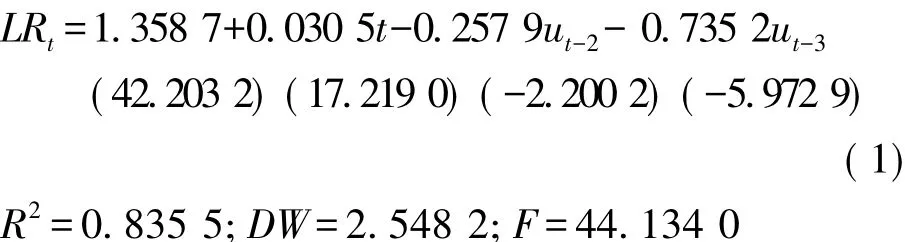
式(1)的现实经济意义体现在:t的参数0．0305体现了我国真实自然灾害救济费的年增长率为3．05%，而ut-2和ut-3以及其参数体现了取对数的真实自然灾害救济费是前第3期和前第2期的移动平均。根据模型结构，可以得出以下结论。

(1)应该加大灾害救助投入力度。虽然我国逐年加大了灾害救助投入力度，总体来说，救助力度是不够的。首先，根据式(1)中固定时间趋势项的系数，3．05%的增长率是偏低的。此外，救助比例也很低。图2中，RN表示自然灾害救济人数与受灾人数之比，RR表示自然灾害救济费与灾害直接经济损失之比。无论是救济人数的比例还是救济费的比例，都很低。尤其救济费的比例，只有2%～3%，对损失的弥补是杯水车薪。此外，RN相当于RR的5～10倍，救济人数多而经费少，人均救济费非常之低。由此可见，是由受灾单位和个人承担了主要损失。因此，应该进一步加大灾害救助投入力度。可以通过扩大救助对象范围、提高救助经费标准等手段，帮助民众抵御自然灾害。

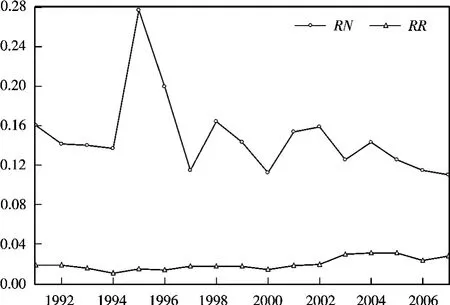
图2 自然灾害救助比例图

(2)改进灾害救助预算方法。目前的灾害救助预算工作，都是根据前一年的数据进行上浮或者下调。由模型可知，实际的灾害救助支出与前一年并没有多大关系，主要与前第二和第三年有关。因此，应该借助ARIMA模型，改进灾害救助预算方法。

五、预测分析

对自然灾害救助支出的预测是制定救灾支出预算的依据，是开展备灾救灾工作的基础，也是提高灾害救助工作绩效的手段，对其进行研究具有重要的现实意义。2006年颁布的《国家自然灾害救助应急预案》要求建立自然灾害救助的资金自然增长机制，即灾害救助资金保持一定的增长比例。该方法显然存在以下不足:1)忽视了价格水平变化。改革开放至今，我国物价指数上升迅速。因预算增长比例低于物价上涨比例，使得很多年份救灾支出明升实降。2)不能反映波动情况。灾害救助支出是一个随机过程，存在波动。固定比例增长不能把握其波动规律，在多灾年份会预算不足，少灾年份会预算浪费。为此，应该采用更为科学的预测方法。实践证明，在短期预测中，ARIMA模型准确率很高。因此，本文将以此模型进行短期预测。

在不发生结构突变的情况下，也就是现有灾害救助体制不发生大的改变的情况下，利用MA(3)模型进行预测，在95%置信水平上，2008—2010年的真实自然灾害救济费预测值见表4。由表4可知，接下来的三年，NDR支出会进一步增加。尤其是2008年和2010年，增支的幅度会很大。因此，这两年应该大幅度增加预算，加强备灾工作力度。当然，预测所提供的是真实值，具体名义值的计算还要考虑当年的价格指数。

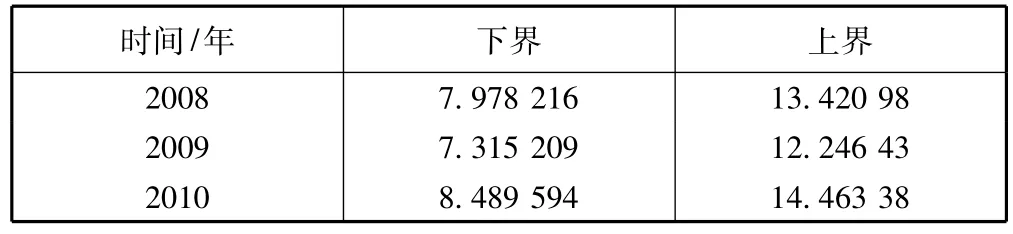
表495%置信水平的预测值

六、研究展望

不断发生的各种自然灾害考验着我国的灾害救助体制，而如何提高灾害救助支出效率始终是灾害救助体制核心问题之一。提高灾害救助支出的效率，需要从“质”和“量”两方面着手。本文以ARIMA(0，0，3)模型对我国灾害救助支出进行了预测，主要从“量”的角度进行了探索。至于“质”的方面，主要考虑救灾支出的结构和方式。事实上，国外有相关经验可资借鉴。日本重视防灾，投入了大量资金用于防灾设施和防灾教育，建立了严密的监测网络，举行各种形式的防灾演习，并建有许多防灾体验中心［10］。这些方式提高了防灾能力和人们灾中自救能力，降低了灾害损失。美国有多种灾害救助方式供灾民选择，诸如个人低息贷款，中小生意援助计划等［11］。这些灵活的救助方式，不但很好地救济了灾民，还给了他们灾后创业的机会。应该充分吸收这些先进经验，积极探索适合我国的救灾支出结构和方式，这将是未来可能的研究方向。

［1］ 孙 婧．灾害救助方式的政府决策［J］．中国减灾，2006(10):32-33．

［2］祁 毓．我国自然灾害救助财政投入现状、问题及对策［J］．地方财政研究，2008(1):25-28．

［3］ 郭显光．救灾支出分配模型及应用［J］．数量经济技术经济研究，1998(12):48-51．

［4］郭显光．浙江省救灾支出管理决策支持系统设计思路［J］．温州大学学报，2003(2):22-25．

［5］赵卫亚．救灾资金需求分配的统计分析［J］．统计与决策，1998(12):14-15．

［6］Box George E P Jenkins G M．Time Series Analysis:Forecasting and Control［M］．San Francisco:Holden-Day;1976．

［7］ 王振龙，胡永宏．应用时间序列分析［M］．北京:科学出版社，2007:7-8．

［8］Pindyck S R，Rubinfeld L D．Econometric Model and Economic Forecasts［M］．New York:McGraw-Hill Companies:1998．

［9］ 张晓峒．计量经济分析［M］．北京:经济科学出版社:2000．

［10］佚名．日本抗震救灾经验［J］．资源与人居环境，2008(11):22-22．

［11］陈 浩．美国的救灾应对程序与ngo的力量［J］．中国减灾，2008(8):42-43．

China's Natural Disaster Relief Expenditures Based on ARIMA Model(1978—2007)

ZHAO Li-ming，WANG Zhong
(School of Management，Tianjin University，Tianjin 300072，China)

Time series analysis is made on data of China's natural disaster relief expenditures from 1978 to 2007．And the result indicates that ARIMA(0，0，3)model is fit for China's disaster relief expenditures modeling．Through modeling and combining statistical data on the ratio of accumulative number of persons appealing to disaster relief to population affected by disasters，as well as the ratio of relief funds for natural disasters to econmomic loss in natural disasters，we make structure analysis and put forward relevant proposals to improve natural disaster relief．Finally，short-term forecasting was made based on the model．

natural disasters;relief expenditures;ARIMA model

F224．9

A

1008-4339(2010)03-0193-04

2009-01-13．

教育部科学技术研究重点基金资助项目(00024)．

赵黎明(1951— )，男，博士，教授．

赵黎明，zhaolm@tju．edu．cn．