非线性检验及预测在污水处理厂评价中的应用

张世英，李 琦

(天津大学管理学院，天津 300072)

非线性检验及预测在污水处理厂评价中的应用

张世英，李 琦

(天津大学管理学院，天津 300072)

为了避免污水处理厂规模盲目扩大造成的投资效率低下的现象发生，科学地预测合理的用水量必不可少。基于用水量的实际历史数据，利用BDS检验、Box-Pierce检验和Box-Ljung检验以及非线性检验，如代替数据检验Surrogate date test、Hinich双谱检验、White人工神经网络检验来选择时间序列重构预测模型。根据实际用水量情况，比较各种不同重构模型预测误差，包括线性AR模型以及随机森林、随机梯度Boosting、支持向量、人工神经网络和自适应样条等。结果表明，有着非线性关系的人工神经网络误差最小，符合检验结果。

用水量;非线性检验;预测;随机梯度Boosting

在污水处理厂的建设中，一般会结合经济发展和城市建设的总体规划来考虑污水处理厂的建设规模，并以近期需求为主，适当考虑长远发展的需要来确定污水处理厂的使用周期。建设部已经要求各地保证城镇污水处理厂投入运行后的实际处理负荷在一年内不得低于设计能力的60%，三年内不得低于设计能力的75%。目前，许多地方盲目追求政绩，不考虑实际情况，任意扩大污水处理厂建设规模，致使建成的污水处理厂大部分处理能力闲置和投资资金效率低下的情况屡见不鲜。为了合理评价污水处理厂的建设规模，有必要对污水产量进行科学预测。

通常情况下，污水处理厂的建设规模以本地排水管理处多年的观测、调查、统计和分析污水量的结果为基础，根据排水规划的服务面积、污水量标准并结合总体规划，同时参考供水指标和供水规划来确定。在以上计算过程中，人均日用水量是个很重要的指标，关系生活用水和公建用水的预测。能否科学准确预测未来年份人均日用水量，很大程度上决定了建设规模的合理性。目前用水量预测模型选择过于随意，缺乏必要的检验［1-2］。本文利用各种非线性检验方法，确定合理预测模型，提高预测精度。

一、检验思路

从统计建模方面考虑，预测方法主要有两种:一是利用历史数据预测未来数值，典型方法就是时间序列;二是利用其他相关数据预测该类指标未来数据。第二类预测方法所需数据较多，由于各种原因，不少城市缺乏生活用水资料，不易搜集数据。所以本文采用人均日用水量的历史数据序列预测未来年份用水量。

时间序列预测法的基本特点:一是假定事物的过去趋势会延伸到未来;二是预测所依据的数据具有不规则性;三是撇开了与其他因素之间的因果关系。

给定一组数据选择合适模型预测未来取值主要从以下三个方面考虑:一是数据的经验特征是否符合模型的前提条件，如ARMA模型要求序列是平稳的;二是模型拟合之后的假设检验是否显著，如线性回归的显著性检验;三是如果数据足够充分，可以把数据分成两部分，一部分用于建模，另一部分用于检验拟合模型预测的精度。

时间序列各种模型一般要求序列平稳，而原始序列由于存在长期趋势和周期趋势等，是非平稳的。必须通过变换使其平稳化，通常的一种变换是变化率变换 lnXt－lnXt－1，它的一阶泰勒展开就是变化率(Xt－Xt－1)/Xt－1。虽然不同城市之间人均日用水量存在一定的差别，但是其变化率相差不大。考虑到国内城市用水资料搜集的困难性，采用澳大利亚Mawson地区2000年1月到2007年4月每月人均日用水量数据，数据长度88。基于其变化率预测其他城市人均日用水量变化率，逆变换得到原始用水量。

基于 BDS 检验［3］、Box-Ljung 检验［4］、Hinich 双谱检验［5］、代替数据检验［6］、White 人工神经网络检验［7］等方法辨识时间序列内在变化模式，首先，判断序列之间独立还是相关，如果相关，然后进一步检验线性相关和非线性相关。这里存在两种方法:一是直接判断线性和非线性，如代替数据检验和Hinich双谱检验;二是剔除线性相关性，如果残差独立同分布，表明原始序列线性相关，如果残差继续存在相关性，表明原始序列非线性相关，所以独立性检验也可用于检验线性和非线性，如果非线性相关，还可以进一步判断是否存在混沌。通过各种检验方法判断人均日用水量变化率的变化模式，建立合理的线性或者非线性模型，预测未来人均日用水量变化率。假定不同城市人均日用水量变化率具有相同的变化模式，根据很少的用水资料可以预测未来年份人均日用水量，为合理评价污水处理厂建设规模提供参考，力求评价的科学性和准确性。

二、检验结果

澳大利亚Mawson地区2000年1月到2007年4月每月人均日用水量数据从澳大利亚数据中心http://aadc-aps．ad．gov．au/aadc/soe/displayindicator．cfm?soeid=61#graph查询得到。采用KPSS进行平稳性检验，统计量结果为0.058，对应相伴概率为0.10，结论是平稳的。BDS检验独立性检验相伴概率与嵌入维数和相邻点判断参数有关，不同组合的相伴概率不尽相同。因为拒绝是有力的，而接受只是表示在目前水平下不拒绝原假设，所以只要有一个组合拒绝原假设，即可认为拒绝原假设，表示时序不是独立同分布的，存在相关性或者独立不同分布。BDS检验结果表明，日用水量变化率独立不同分布或者相关。为了进一步检验是否存在相关性，采用Box-Pierce和Box-Ljung独立性检验，两者相伴概率都小于0.05，在5%的显著性水平下，拒绝原假设，认为人均日用水量变化率具有相关性。

判断相关是线性相关还是非线性相关，应采用代替数据检验。本文采用Schreiber等人［8］的IAAFT算法产生100组代替数据，检验统计量取平均互信息指数。检验结果表明，在5%置信水平下不能断定人均日用水量变化率存在非线性相关。

考虑弱非线性检验——White人工神经网络检验和Terasvirta人工神经网络［9］，不是均值线性的时间序列称为“弱非线性”。两种检验方法的相伴概率都小于5%，拒绝原假设，说明人均日用水量变化率确实不是均值线性，存在弱非线性相关。

Hinich的双谱检验可以直接检验三阶非线性和正态性。计算得到人均日用水量变化率双谱非线性检验的相伴概率为1.0，不认为其具有三阶非线性。

由于White人工神经网络检验和Terasvirta人工神经网络检验本文人均日用水量变化率存在弱非线性，为了进一步判断是否存在混沌，需要计算时间序列的最大Lyapunov指数。利用Rosenstein等人［10］方法和Nychka等人［11］的人工神经网络估计最大Lyapunov指数。Rosenstein等人的方法首先需要确定嵌入维数m和时间延滞d。它们也是相空间重构中最重要的两个参数。在预测过程中，采用相空间重构方法恢复原始动力系统。本文首先基于平均互信息指数确定最佳时间延滞d，然后采用虚假最近邻法确定最优嵌入维数m。最佳时间延滞d应取2，最优的嵌入维数m是3。用Rosenstein等人方法估计最大Lyapunov指数为0.373 6左右，Nychka等人人工神经网络估算的Lyapunov指数为0.263 5。一般只是Lyapunov指数的符号判断混沌是否存在，由Lyapunov指数为正，说明人均日用水量变化率存在混沌。

三、用水量预测

通过计算，估计最优的时间延滞为2，嵌入维数是3，所以重构模型为

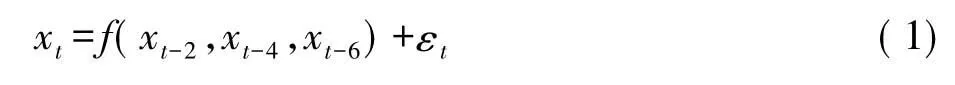
式中:xt为重构模型;f为未知非线性函数;xt－2，xt－4，xt－6为 t－2，t－4，t－6 时刻指标取值;εt为随机噪声。

机器学习的方法有多种，这里选取成熟稳定的随机森林、随机梯度Boosting、支持向量、自适应样条和人工神经网络5种方法。由于用水量数据只是弱非线性，可以考虑线性时间序列的AR模型。为了从上述方法中选择一种较好的方法，预留最后7组数据不用来训练，比较7组预留数据的相对误差，预测值减去真实值除以真实值，选择一种评比原则，得出较优方法。

前面已经检验过用水量变化率的平稳性，所以不用差分模型，直接选取AR模型。最优嵌入维数为3，选取AR(3)模型。对于标准残差不同滞后阶数的Box-Ljung独立性检验，易知相伴概率都大于0.05，不能拒绝原假设，表明标准残差独立，选用AR(3)模型合理。从预留7组数据的相对误差的均值和方差来看，人工神经网络都是最好的方法。在误差比较中，一般人们只关心误差的绝对大小，而不太重视正负符号。如果单纯考虑相对误差绝对值，其均值和方差最小的还是人工神经网络，认为人工神经网络更适用于本文用水量数据。

在向后预测过程中，由于重构模型中自变量也是随机变量，加上噪声的干扰，每步预测的标准误差不固定。由于人工神经网络模型的复杂性，推导每步预测值的标准误差无法完成。采用蒙特卡罗方法模拟。蒙特卡罗方法的思想是产生服从概率分布的伪随机数，代入复杂函数表达式，所得结果的经验分布当作所求分布的估计。预测值的不确定性来源于两个方面:一是具有固定标准差σ的噪声;二是重构模型中自变量值的随机性。噪声的标准差σ可以通过残差平方和估计。具体步骤如下:一是利用拟合残差平方和估计噪声标准差σ;二是产生2 000个零均值，标准差为σ的正态白噪声;三是将前面预测值和噪声代入拟合的人工神经网络重构模型，得到2 000个新预测值;四是逆变换人均日用水量变化率到原始人均日用水量，exp(t时刻人均日用水量变化率)乘以t时刻人均日用水量得到t+1时刻原始人均日用水量;五是重复步骤二至四，直至达到需要预测的步数;六是对于每步预测，都存在2 000个预测值，其经验标准差就看作该步预测的标准误差。95%经验置信区间看作该步预测值95%置信区间。

为了验证预测结果的可靠程度，从网站http://aadc-maps．aad．gov．au/aadc/soe/display indicator．cfm?soe id=61#graph上查询2007年5月到2009年5月Mawson地区月人均日用水量数据，基于人工神经网络训练结果，预测2007年5月到2009年5月Mawson地区月人均日用水量见图1。以散点表示的是真实用水量，中间有缓慢增长趋势，以长虚线表示的是预测均值，上下短虚线是预测值的95%置信上限和下限，体现用水量预测波动的水平。从图1中可以看出，真实用水量除去一个点在预测95%置信区间之外，其他所有点都在预测95%置信区间之内，证实了本文预测的可靠性。

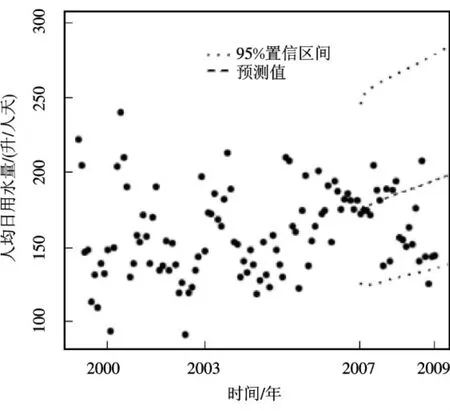
图1 人均日用水量及预测值

四、结 语

污水处理厂一般存在近期和远期规模，远期规模需要预测才能合理评价。人均日用水量是确定污水处理厂建设规模的一个重要指标，利用BDS检验、Box-Pierce检验和Ljung-Box检验等独立性检验，判断人均日用水量时间序列存在相关性。代替数据检验不能确定非线性相关，Hinich双谱检验也不能确定三阶非线性相关，而White和Teravitra人工神经网络检验判断出弱非线性。计算Lyapunov指数为正，存在混沌。由于存在弱非线性，基于相空间重构，利用随机森林、随机梯度Boosting、支持向量、人工神经网络、自适应样条和线性AR模型6种方法拟合原始动力系统。在预留七组数据中，人工神经网络预测相对误差的均值和方差最小，最后基于人工神经网络拟合结果，预测后两年人均日用水量。

［1］ 王洪礼，韩红臣，李胜朋，等．城市用水量随机梯度回归分析［J］．天津大学学报:社会科学版，2008，10(3):225-227．

［2］ 李 栋，王洪礼，杜忠晓．城市生活用水的支持向量回归预测［J］．天津大学学报:社会科学版，2006，8(1):64-67．

［3］ Brock W A，Dechert W D，Scheinkman J A．A Test for Independence Based on the Correlation Dimension［R］．Madison:University of Wisconsin-Madison，1986．

［4］ Ljung G M，Box G E P．On a measure of lack of fit in time series models［J］．Biometrika，1978，65:553-564．

［5］ Hinich M．Testing for Gaussianity and linearity of a stationary time series［J］．Journal of Time Series Analysis，1982，3(3):169-176．

［6］ Theiler J，Eubank S，Longtin A，et al．Testing for nonlinearity in time series:The method of surrogate data［J］．Physical D Nonlinear Phenomena，1992，58:77-94．

［7］ White H．An additional hidden unit test for neglected nonlinearity in multilayer feed-forward networks［C］//Proceedings of the International Joint Conference on Neural Networks．New York:IEEE Press，1989(2):451-455．

［8］ Schreiber T，Schmitz A．Improved surrogate data for nonlinearity tests［J］．Physical Review Letter，1996，77(4):635-638．

［9］ Teraesvirta T，Lin C F，Granger C W J．Power of the Neural Network Linearity Test［J］．Journal of Time Series Analysis，1993，14:209-220．

［10］ Rosenstein M T ，Collins J J，Luca C J D．A practical method for calculating largest Lyapunov exponents from small data sets［J］．Physical D，1993，65:117-134．

［11］ Nychka D，Ellner S，Gallant A，et al．Finding chaos in noisy systems［J］．Journal of Royal Statistical Society B，1992，54(2):399-426．

［12］ 张 维，杨旭才，陆晓春，等．污水处理厂机器学习综合评价［J］．天津大学学报:社会科学版，2008，10(2):118-121．

Application of Nonlinearity Test and Prediction in Assessment of Sewage Disposal Plants

ZHANG Shi-ying，LI Qi
(School of Management，Tianjin University，Tianjin 300072，China)

Scientific prediction of reasonable water consumption is inevitable to avoid blind expansion in sewage disposal plants with low efficiency of investment．Historical data were collected．Independent tests such as BDS，Box-Pierce and Box-Ljung tests and nonlinearity tests including surrogate data，Hinich's bispectrum and White's artificial neuron network tests were applied jointly．The reconstruction prediction model is selected through these tests．The prediction errors of AR，random forest，stochastic gradient boosting，support vector，artificial neuron network and multivariate adaptive regression splines were calculated based on real consumption．The results show that artificial neuron network with nonlinear relation exhibits the minimal error，which accords with the conclusion of all tests．

water consumption;nonlinearity test;prediction;stochastic gradient boosting

X730

A

1008-4339(2010)04-0318-04

2009-10-20．

国家自然科学基金资助项目(10772132);中国博士后科学基金资助项目(20060400706)．

张世英(1936— )，男，教授．

李 琦，liqifree2003@yahoo．com．cn．