极值理论高频VaR区间估计模型的构建
2010-09-19刘峥然张亚楠
赵 息,刘峥然,张亚楠
(天津大学管理学院,天津 300072)
极值理论高频VaR区间估计模型的构建
赵 息,刘峥然,张亚楠
(天津大学管理学院,天津 300072)
为了对在险值的估计精度进行度量,更为精确和有效地衡量极值VaR(value at risk)的估计风险,基于广义极值理论构建了极值VaR的区间估计模型,并进一步利用高频数据重点考察了不同置信水平和不同样本容量分块下的极值VaR区间估计结果的精度和模型的有效性。结果表明,极值VaR的动态区间估计模型与参数法和非参数法区间估计模型相比,不仅能够更为有效地捕获极端条件下收益率时间序列的动态特征,而且具有很好的估计精度,VaR估计风险的精确度更高。
置信区间;极值VaR;广义极值分布;高频数据
近年来,金融市场自由化使得全球金融环境更加具有风险,作为风险管理国际标准的VaR是金融市场风险测量的主流模型,巴塞尔协议和欧盟资本充足率指导都已使用VaR作为监督标准。金融市场风险管理主要是关注收益率分布的左尾,它反映了潜在发生概率极小但却蕴含巨大风险损失或者灾难性后果的极端事件,目前正严重冲击着全球金融市场的次贷危机也暴露了金融机构在防范蕴含巨大损失的极端事件方面的缺陷,因此对金融风险极值理论的研究是非常必要的。
Danielsson等[1]指出,一个好的 VaR模型应该能够基于历史样本提供更为平滑的尾部估计和正确的表示出极端事件发生的可能性。在过去几年中,各种各样的金融极端事件使得金融机构不得不通过识别与防范这类事件而重新对金融风险进行建模,从而达到优化风险管理系统的目的。因此,最近对于VaR的研究关注于收益分布的尾部特征,基于风险极值理论的VaR建模研究为构建更为精确的VaR点估计方法提供了新思路,Bystrom[2]和 Fernandez[3]实证分析结果也表明了对于厚尾分布极值理论估计VaR比其他估计方法更精确。
但是,更为完善的金融市场风险管理不仅仅需要VaR的点估计方法,还需要对VaR的估计精度进行度量。VaR点估计本身存在的风险主要来源于样本的波动或者模型本身参数设定的不适用性。Jorion[4]首次利用置信区间的概念探讨VaR估计的风险问题,并在一些简单的收益率分布模型假设下,推导出VaR的近似置信区间。随后,Huschens[5]也有一些相关研究结果。在其他风险值估计方法方面,一些学者研究了使用次序统计量理论,如Dowd[6]等计量方法对VaR置信区间进行估计建模。国内学者对于VaR区间估计的评判研究才刚刚起步,还有待进一步深入。马玉林[7]使用沪市周、月收益率利用不同分布来估计VaR的置信区间。通过以上文献分析可以看到,在国外发展迅速的极值VaR理论在点估计研究方面的优势已得到了学术界的普遍认同,但是对于极值VaR置信区间的研究还鲜有涉及。
在上述研究的基础上,基于包含更多信息的高频数据,在极值分布基础上建立极值VaR的置信区间的估计模型,并利用这一解析解对不同置信水平及不同分块标准下的极值VaR的置信区间进行实证估计,以期在捕获极端条件下收益率时间序列动态特征的基础上,更为精确和有效地衡量极值VaR的估计风险。
一、极值VaR置信区间模型构建
1.极值VaR的点估计
若假定一个随机变量X,其分布函数为F,代表在一定时期内某项金融资产的损益,则VaR可表示为分位数的形式,即VaR=F-1(1-p)。其中p为置信水平;F-1(1-p)为F的反函数,即p分位数。因此,只要得到一定时期内的分布函数,就可以计算相应VaR的值。
当研究金融资产极端情况下的VaR时,假设Pt表示资产在时间t时的价格,R(q),t表示一天内等间隔的q个收益,即
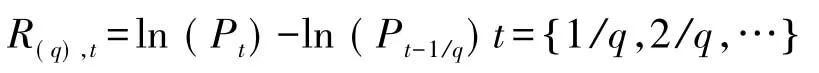

且极值变量m分别服从广义极值分布(GEV),即
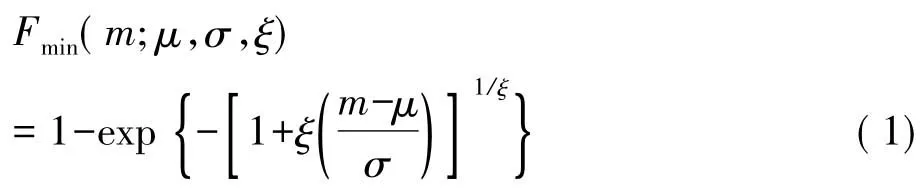
式中ξ、μ、σ分别为形状参数、位置参数和尺度参数。
m的广义极值分布的概率密度分布为

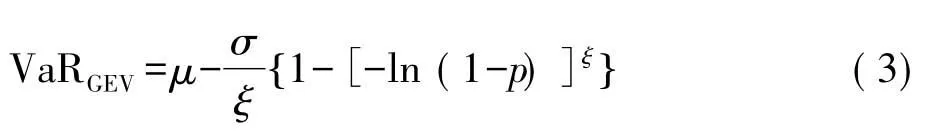
记其中待估参数 θ=(μ,σ,ξ)T,使用极大似然估计可以得到^θ=(^μ,^σ,^ξ)T,其中似然函数表达式为
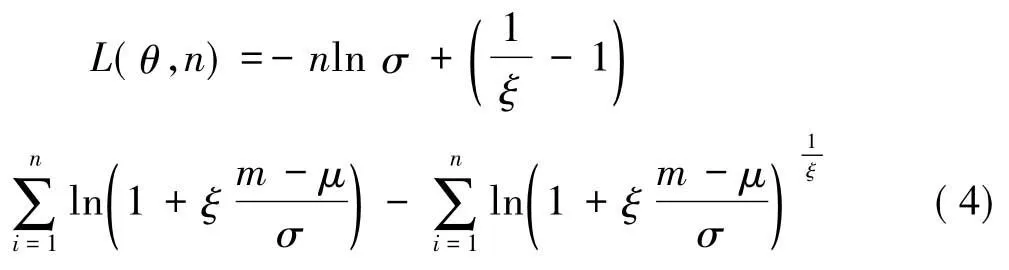
在以上极值分布的基础上可以得到极值VaR为
2.VaR置信区间的设定
进一步根据极大似然估计的统计推断理论,如果样本量足够大,最大似然估计^θ可由下式表示,即


二、实证分析
1.数据选取与基本统计描述
本文选用了上海证券交易所综合指数作为样本数据,选取2005年1月 3日至 2007年12月 28日共34 722个5 min收益作为模型的估计样本。由于广义极值分布的分块频率选择会对位置参数和尺度参数估计结果产成较大影响(Broussard和 Booth[9]),并且最优分块标准也没有统一结论,因此,选取 5 min、30 min、60 min和240 min作为分块标准(见表1)。

表1 收益率统计描述
表1是对收益数据的基本统计,从不同分块方法中可以看出,样本的均值及标准差都有随着时段的增加而明显增加的趋势,均值的增加和我国数据年度股票市场的整体上涨趋势相一致,标准差的增大表明大块样本具有更加明显的波动。而且随着时段的增加,偏度、峰度以及ADF统计量都有较明显的下降趋势,表明高频数据,尤其是5 min数据表现出最明显的尖峰厚尾特征。
2.广义极值分布的置信区间估计
本文首先使用全样本在不同的分块标准下通过极大似然估计得到广义极值分布的位置参数、尺度参数以及形状参数,不同分块标准的估计结果(见表2)。
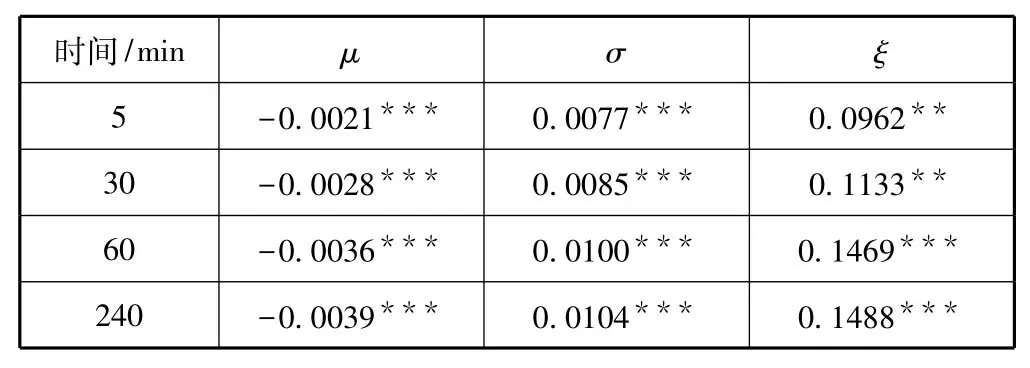
表2 不同分块方法广义极值分布的参数估计结果
如表2所示,广义极值分布估计的大部分参数结果在5%置信度下显著,其中μ、σ在1%置信水平下均显著。μ的估计结果具有减小的趋势,这也同分块时段增加时其极小值一般会大于分块时段减小时的极小值相一致。σ的增大也表明随着时段增大样本的波动加剧。因此,从参数估计结果可以看出,这种方法可以更好地描述高频数据极值具的尖峰厚尾特征。
为了比较不同置信水平和不同分块标准下极值VaR估计值之间的区别,我们先用23 022个观测值作为训练数据来估计模型的各个参数,然后作5次一步预测计算VaR值。接着估计窗口向前滚动,得到一组新的参数值,进而对接下来的5个交易日作一步预测计算极值VaR,这一过程持续到预测区间的最后一天,即2007年12月28日。
使用图1来比较在5 min分块条件下置信水平分别为95%和99%时极值VaR与日收益的走势,图2为置信水平为95%时3种不同分块条件下VaR与日收益的比较图。
从图1可以看出,极值VaR值在收益波动加剧时明显增大,且99%较95%变化更为明显,从图2可以看出,极值VaR估计值随着分块时段的增加波动更加剧烈,这表明极值VaR能够考虑到当前的预期和波动性,能够较为敏感地捕捉到收益的动态性。
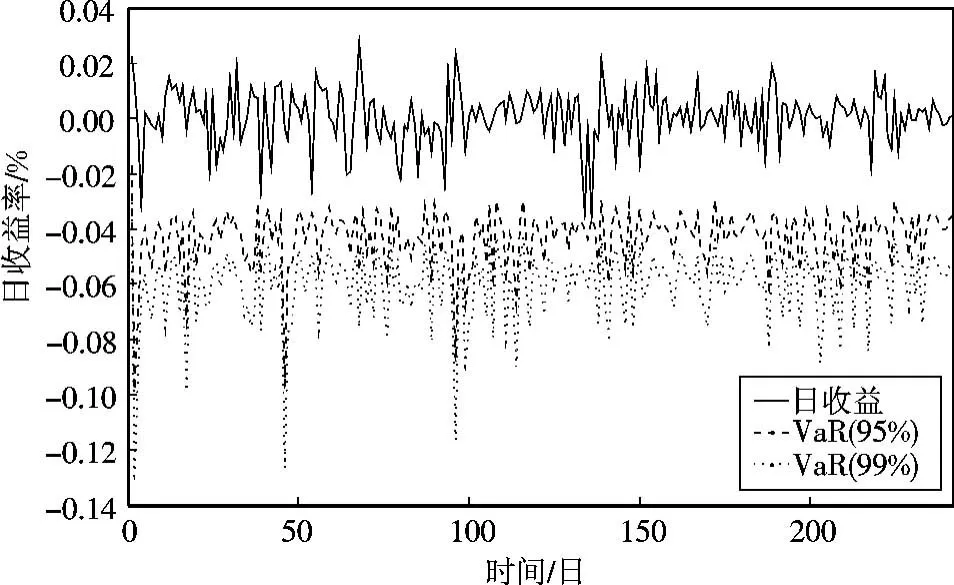
图1 5 min分块条件下极值VaR与日收益
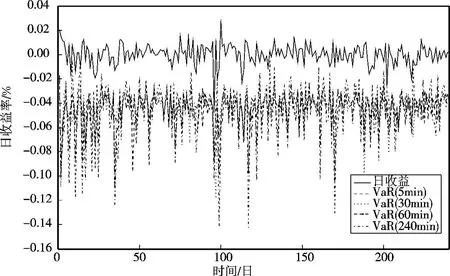
图2 3种不同分块条件下极值VaR与日收益
广义极值VaR的点估计只能根据收益波动的变化来调整VaR的估计值,当市场产生较大波动的情况下,并不能探讨估计值的误差风险,置信区间为探讨VaR值的风险问题提供可能。仍然采用上述极值VaR的预测区间进行滚动置信区间估计,表3为不同置信水平下不同分块标准对应的VaR估计的置信区间的下界、上界及区间宽度值的均值描述。

表3 不同置信水平下不同分块标准置信区间的均值描述
从表3可以发现不同置信水平下不同分块标准置信区间宽度的数量级均在10-3,较短的区间宽度表明模型具有很好的估计精度且估计值具有较小的方差。99%的置信水平下的区间宽度要明显大于95%的置信水平下的区间宽度,而且随着分块时段的增加,区间宽度逐渐变大,这表明当取较大的分块时,分块观测值得减少降低了参数估计的有效性,而且这也同图2所示极值VaR估计值随着分块时段的增加波动更加剧烈相一致,随着波动的加大,极值VaR估计的精确度下降,区间宽度的增大就表明估计值的方差的变动。因此,极值VaR的置信区间的估计模型可以很好地度量极值VaR在点估计过程中的误差风险,在市场波动加大时更好地综合评价风险价值。这也表明对于较大的市场波动,风险管理者要更谨慎地对待已估计的VaR值,综合考虑VaR的估计风险以提高和完善金融市场风险管理水平。
3.广义极值分布的置信区间估计有效性
现存的VaR模型主要可以分为参数模型(如正态分布模型、Risk-Metrics模型等)、非参数模型(如历史模拟法和混合模型等)以及半参数模型(如极值理论等)这三类,因此为了检验广义极值分布置信区间估计的有效性,进一步使用正态分布模型和历史模拟法对同一时间段上海证券交易所综合指数的日收益进行VaR的置信区间估计,估计结果见表4。
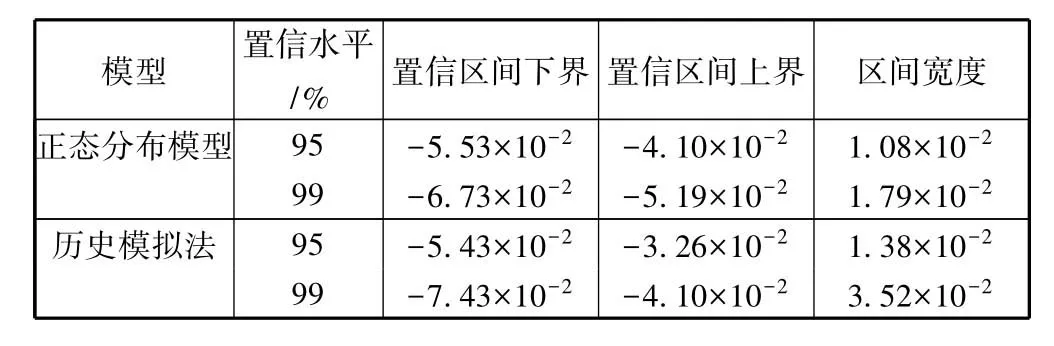
表4 正态分布模型和历史模拟法的VaR置信区间估计结果
由表4可以看到正态分布模型和历史模拟法的置信区间宽度的数量级普遍在10-2,均大于表3中我们使用基于广义极值理论构建的极值VaR的置信区间估计模型得到的区间宽度数量级为10-3的估计结果。而且可以注意到历史模拟法在99%的置信水平下存在明显的风险高估现象,预测结果很不稳定。但是本文中所构建的对极值VaR的置信区间的估计模型不仅是对极值VaR的动态置信区间进行估计,而且具有更好的估计精度,能考虑到当前地预期和波动性,能够较为敏感地捕捉到收益的动态性。
三、结 语
为了对在险值的估计精度进行度量,本文基于广义极值理论建立了极值VaR的区间估计模型,得到了极值VaR置信区间的解析解的一般形式,更为精确和有效地衡量极值VaR的估计风险。利用高频数据重点考察了不同置信水平和不同样本容量分块下的极值VaR区间估计结果的精度和模型的有效性。结果表明,由于广义极值分布的自身特征,不同的置信水平和分块结果会对极值VaR的置信区间的估计结果产生明显的影响;正态分布模型和历史模拟法的置信区间宽度的数量级均大于使用基于广义极值理论构建的极值VaR的置信区间估计模型得到的估计结果。因此,本文中所构建的对极值VaR的置信区间的估计模型不仅能够更为有效地捕获极端条件下收益率时间序列的特征,而且具有很好的估计精度,更为精确地描述VaR的估计风险。
[1] Danielsson J,Vries C D.Value-at-risk and extreme returns[R].London:London School of Economvcs,1997.
[2] Bystrom H N E.Managing extreme risks in tranquil and volatile markets using conditional extreme value theory[J].International Review of Financial Analysis,2004(13):133-152.
[3] Fernandez V.Risk management under extreme events[J].International Review of Financial Analysis,2005(14):113-148.
[4] Jorion P.Risk2-measuring the risk in value at risk[J].Financial Analyst Journal,1996,52:45-56 .
[5] Huschens S.Confidence intervals for value at risk[J].Risk Measurement, Econometrics and Neural Networks, 1997(12):233-244.
[6] Dowd K.Estimating VaR with order statistics[J].Journal of Derivatives,20013,(8):23-30.
[7] 马玉林,周 林.沪市VaR估计误差及其实证[J].统计与决策,2005(11):99-101.
[8] Sen P K,Singer J M.Large Sample Methods in Statistics:An Introduction with Applications[M].New York:Chapman and Hall,1993.
[9] Booth G G.Prudeut margin levels in the finish stock index markot[J].Management Science,1997,43:1177-1188.
Interval Model Estimation of VaR of High Frequency Extreme Value
ZHAO Xi,LIU Zheng-ran,ZHANG Ya-nan
(School of Management,Tianjin University,Tianjin 300072,China)
In order to capture the character of return series in extreme condition and improve VaR(value at risk)precision,a model of extreme value VaR is established.Aolopting high frequency data,the result precision of confidence interval of extreme value VaR and the validity of model are mainly studied under different confidence levels and blocks.The empirical results show that comparing our model with parametric method and non-parametric method in estimation of the confidence interval of VaR,our model can not only captare the risk character of Chinese stock markets,but also achieve better estimation accuracy and describe the estimation risk of the VaR more accurately.
confidence interval;extreme value VaR;generalized extreme value distribution;high frequency data
F224.0
A
1008-4339(2010)-04-0308-05
2009-04-28.
赵 息(1955— ),女,教授.
刘峥然,elvtttca@yahoo.com.cn.
