螺旋桨目标的雷达回波信号相位解缠技术

姜 岩,陈筠力,王 赟

(上海卫星工程研究所,上海 200240)

0 引言

螺旋桨对雷达回波会产生周期性的调制效应。BELL,GRUBBS等建立了喷气式飞机引擎螺旋桨调制效应的数学模型,并由此获得了螺旋桨回波包络的规律[1]。MARTIN,MULGREW对直升机、螺旋桨飞机和喷气式飞机的螺旋桨或旋转引擎的雷达回波频谱进行了特征提取,进而对三类目标进行分类[2、3]。丁建江、张贤达等对基于螺旋桨特征提取的目标识别在防空系统中的应用作了研究[4]。由于从回波频谱中可得目标的周期特征等信息,致使通过研究相位获取目标信息被忽视了。螺旋桨雷达回波相位中含目标的速度、目标螺旋桨的周期特征,以及螺旋桨类型特征等丰富的目标信息,因此研究相位的变化规律对目标识别、多普勒估计,以及螺旋桨飞机成像去干扰均有重要意义。众所周知,雷达接收机常利用正交双通道接收回波。接收机的基带输出是以脉冲重复频率为抽样频率的抽样值,包括I通道和Q(正交)通道的输出。信号中包括的幅值信息不会发生大的变化,但用普通方法求其相位只能得到(0,2π)间的值,即相位的主值,因此需利用某种相位解缠技术将其展开。目前,较常用的相位解缠技术有数值积分算法、SCHAFER的门限算法和TRIBOLET的自适应数值积分算法[5、6]。其中,SCHAFER的算法利用相位主值的跳变将其展开再还原成实际相位,另两种算法均利用相位梯度积分方法还原实际相位。实验表明,桨叶数为奇数和偶数时螺旋桨的雷达回波相位差异非常大。桨叶为奇数时回波相位光滑,适于用积分方式展开,桨叶为偶数时回波相位跳变很大,适于门限算法展开。

螺旋桨回波信号的离散性是形成相位混叠效应的主要原因,而相位解缠技术又受脉冲重复频率过低、飞机飞行速度过大,以及回波相位带宽过大等因素的制约。本文基于经典螺旋桨回波调制模型,研究了螺旋桨雷达回波调制模型的相位解缠技术。

1 螺旋桨雷达回波相位调制模型

1.1 基本回波模型建立

为研究螺旋桨雷达回波的相位在相对运动中的变化规律,建立雷达与螺旋桨相对运动坐标系如图1所示。建模中,省略飞机部分直接给出螺旋桨的结构。设螺旋桨相对雷达以速度v作径向运动,同时以角速度ωp转动;在时刻t,螺旋桨中心相对雷达的距离为R(t);雷达视角即雷达视线与螺旋桨旋转平面的夹角为β。同时建立螺旋桨自身坐标系：螺旋桨旋转平面位于平面XOY(为便于分析,取平面XOY平行于地平面);忽略桨叶螺距角的影响,每个桨叶根部至螺旋桨中心的距离为a,尖端至螺旋桨中心的距离为b,各桨叶形状相同且桨叶间夹角一致。建立回波信号模型所需参数有：雷达与螺旋桨坐标系中心的初始距离R0;R(t)=R0+vt;雷达载波频率f0;雷达载波波长λ;光速c;螺旋桨旋转频率fp;单个螺旋桨的叶片数N。

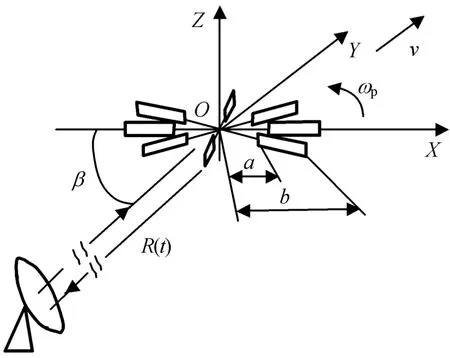
图1 雷达与螺旋桨相对运动Fig.1 Relative motion between radar and propeller

电磁波波长远小于螺旋桨,故可认为雷达的后向散射工作于光学区。则,假设每个螺旋桨叶片均是一强散射中心,N个叶片螺旋桨的雷达回波就可视作N个散射中心的雷达回波的叠加。当不考虑雷达天线扫描形式和螺旋桨叶片螺距角的影响时,螺旋桨的雷达回波可表示为

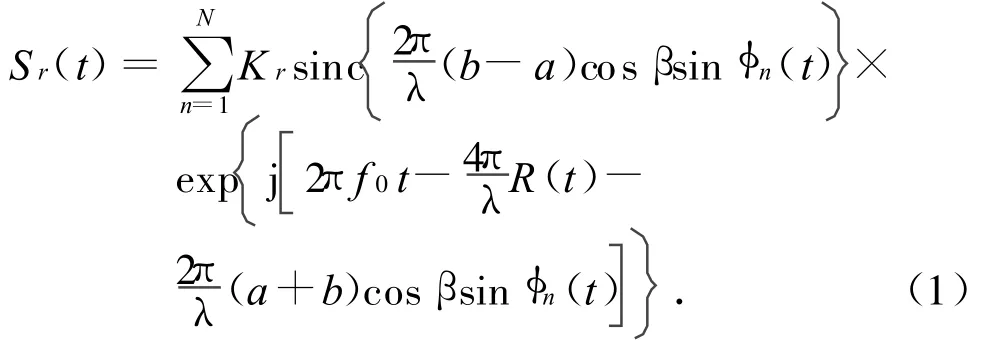
由于载波和初始距离R0对螺旋桨特性的影响较小,且载波的接收亦采用相干方式,可简化公式,去掉相位中的2πf0t项和由R0引起的项,剩余部分用Sb(t)表示,即

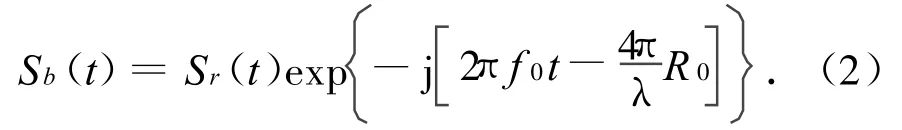
代入式(1),得

式中：fd为多普勒频率,且fd=2v/λ。

由式(3)可知：对单个螺旋桨叶片来说,其雷达回波复包络的幅度部分为周期出现的辛格脉冲函数,该周期与螺旋桨的旋转周期相关,而回波复包络的相位部分为一条以多普勒频率为斜率的直线叠加一正弦周期变化的波动,周期变化规律与幅值相似。

1.2 回波相位特性分析

当飞机距离雷达很远,且飞机平稳飞行时,可认为fd,β近似不变。这样,对单个螺旋桨叶片来说,就可提取其相位因子。设相位部分

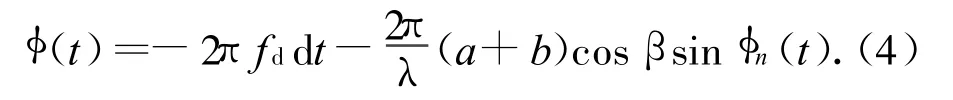
为得到该项的变化规律,选定一组参数进行仿真。

仿真1：设雷达波长3 cm,脉冲重复周期0.1 ms,螺旋桨桨叶长1.2 m,fp=50 Hz,螺旋桨相对雷达运动速度30 m/s,式(4)的仿真结果如图2所示。由图可知：单叶螺旋桨转动引起的正弦波动因多普勒斜率被向下拉长,这与式(3)模型吻合。

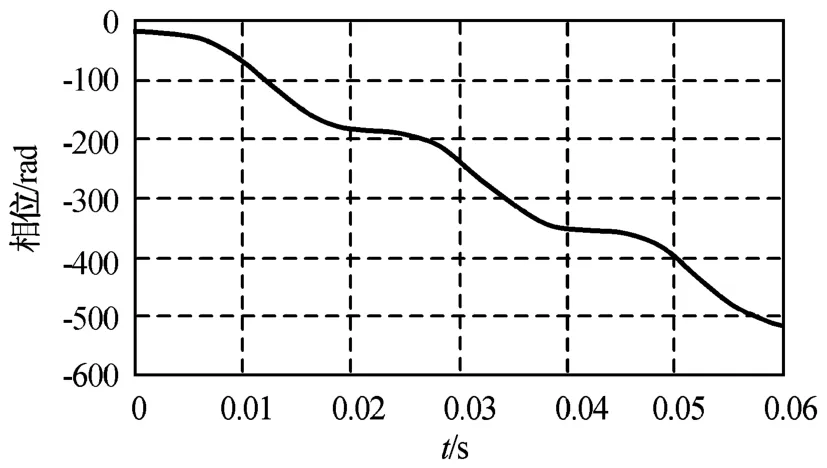
图2 螺旋桨回波模型相位因子Fig.2 Phase of MMBM

实际的螺旋桨至少有2个叶片,涡扇发动机的扇叶甚至有数十个,因此多桨叶螺旋桨回波的相位是本文研究的重点。本文基于式(1)模型,通过改变公式以理解和分析相位的调制特征。理论研究相位结构,需分析N分别为奇数和偶数两种状况。

当N为偶数时(假设N=4,其他N类似),由式(3)可知：螺旋桨上角度相差π的两叶片的回波复包络的幅值(辛格函数)也相差π,即相当于这两项的幅度一样,可将其作叠加合并。对式(3)作变形,分别对n=1,3和n=2,4进行合并,其和式分别为S1,3(t),S2,4(t),则

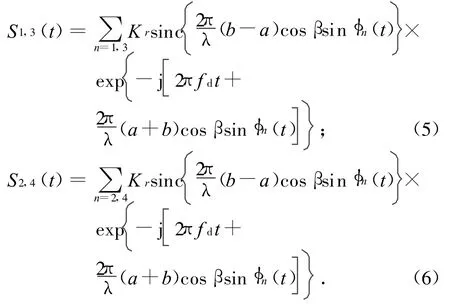
为便于合并,设φn0(t)=2πfpt+φ0,βr1=(ba)cosβ,βr2=(b+a)cosβ,则式(5)、(6)合并后为

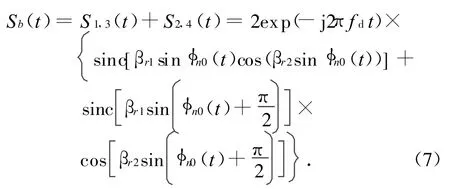
实际上对多数螺旋桨和涡扇来说,桨叶或扇叶的根部均与旋转中心直接相连,即a=0,相当于βr1=βr2。则,式(7)可进一步简化为

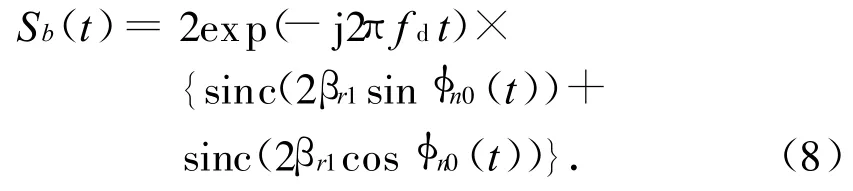
由式(8)可知：其相位由两部分构成。第一部分是以fd为斜率随时间变化的斜线;第二部分由2个实辛格函数组成,相位只能是0或π。因此,偶数片桨叶的雷达回波能使相位上的正弦波动相互抵消。

仿真2：取N=4,其他参数与仿真1相同,仿真结果如图3所示。

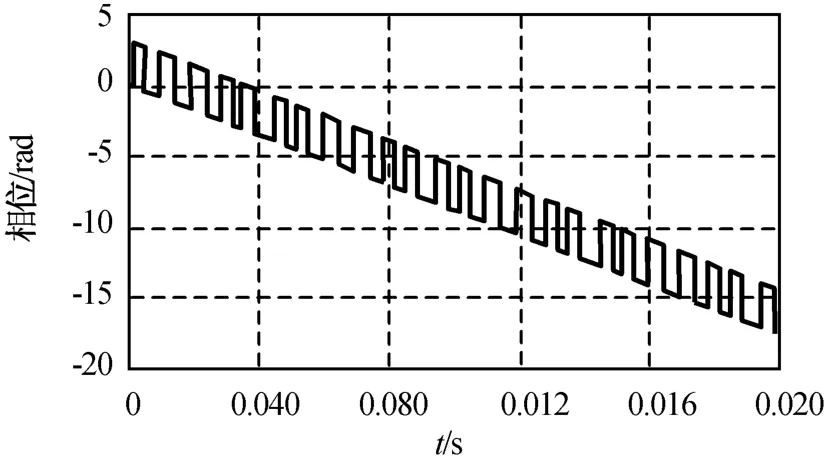
图3 改进模型的螺旋桨回波相位(N=4)Fig.3 Phaseof updated model(N=4)

同理,当N为其他偶数时,同样可得回波模型的简化形式为

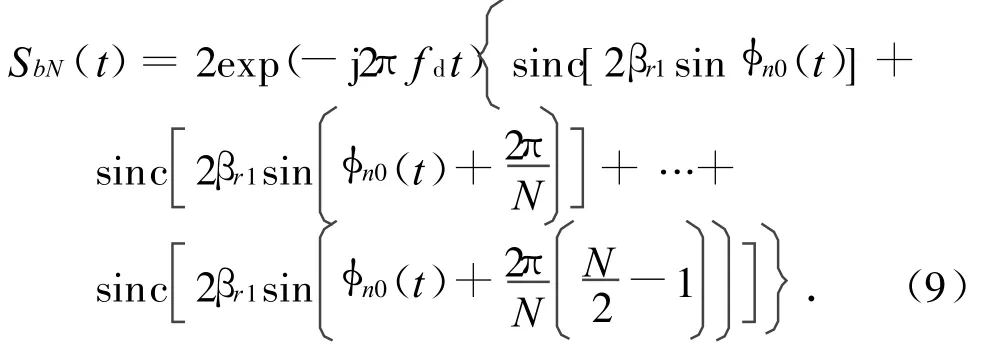
由式(9)可知：除项数增加外,它与式(8)并无大的区别,故其相位亦与式(8)相似,均是以fd为斜率的随时间变化的斜线叠加幅值为π的辛格脉冲函数。

当N为奇数时,螺旋桨各叶片的回波不能合并,桨叶分布的不对称性不能消除回波相位的波动。实际上,奇数片桨叶雷达回波的相位分布与图2相所示的那样分布相似,但N不同会使波动的周期性各异。

2 回波调制模型相位混叠效应分析

2.1 相位混叠效应产生原因

虽然理论相位可由模型而得,但雷达回波的相位不可能直接获得,通常是用正交双通道技术对回波进行相干解调并获得回波复包络的实部I(n)和虚部Q(n)(正交通道)的离散抽样值,其抽样频率即为脉冲重复频率。因此,实际的螺旋桨雷达回波与式(3)不同。用Sb(n)表示回波,则

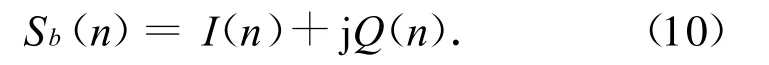
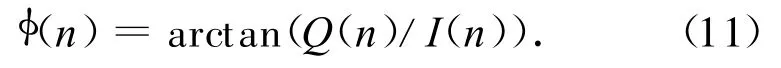
φ(n)的主值取值范围为(-π,π)。

仿真3：取N分别为1,4,其他参数不变,按式(11)对回波相位进行仿真,结果如图4所示。由图可知：相位丢失了原来的规律性,且桨叶数越多,波形就越混乱。相位模糊主要缘于雷达回波的离散性。飞机的飞行速度越大、重复频率越低,回波相位的跳变就越大,相位解缠实施也越难,另外主值相位的大带宽增大了相位解缠的难度。

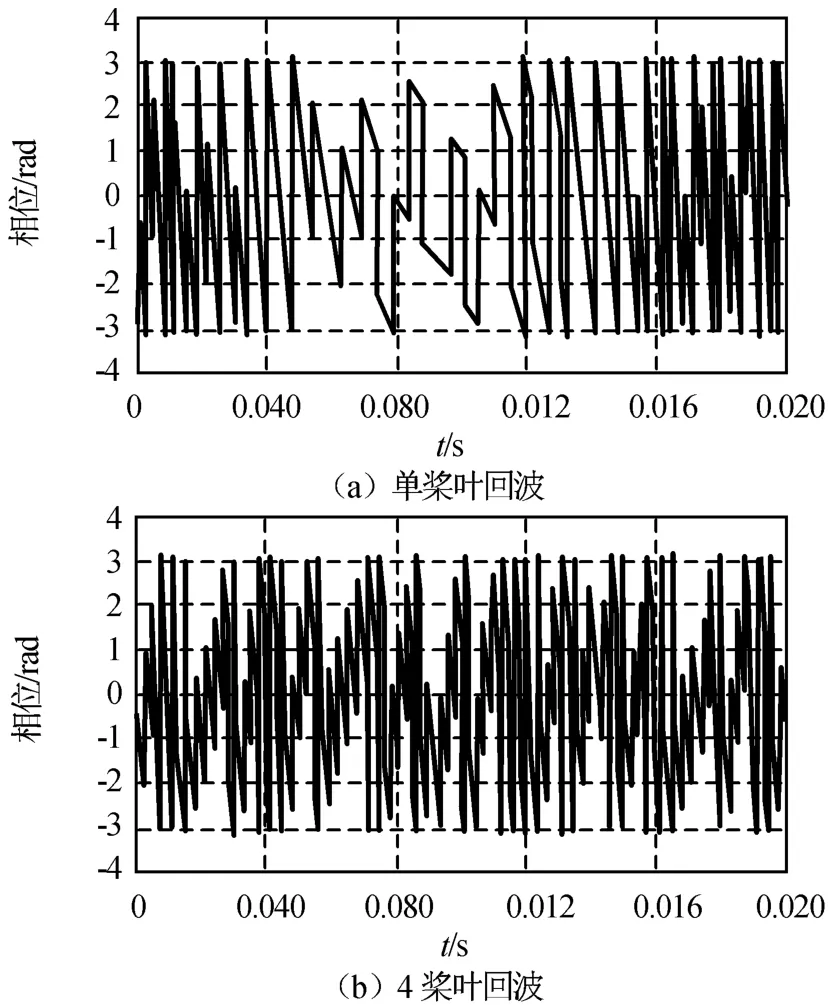
图4 不同时间的螺旋桨回波相位Fig.4 Propeller phaseunder different time

2.2 两种相位解缠方法在螺旋桨雷达回波相位解缠中的应用

针对桨叶数为奇数和偶数时雷达回波相位的特点,本文提出两种相位解缠算法：TRIBOLET的自适应数值积分算法和插值与可调门限相结合的算法。第一种算法根据相位函数的变化快慢自适应调整步长,对相位梯度进行梯形积分实现解缠,但当相位有剧烈跳变或连续性很差时该算法即不再适用,故它适于桨叶数为奇数时的相位解缠。第二种算法适于相位连续性较差变化剧烈状况,可通过相位插值和调整门限减少错误解缠,较适于桨叶为偶数时的相位解缠。

2.2.1 TRIBOLET自适应数值积分算法

设arg Sb(n)为螺旋桨的雷达回波信号的相位主值。若其真实值为φ(n),则时刻n的相位真实值

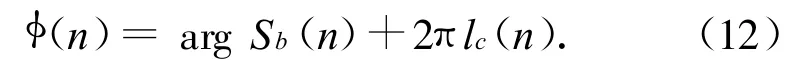
式中：lc(n)为指φ(n)与arg Sb(n)相差lc(n)个2π。只要求出lc(n),相位解缠即完成。

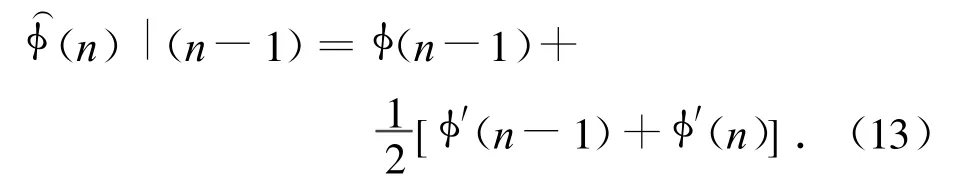
其中,φ′(n)可根据反正切函数求导,即

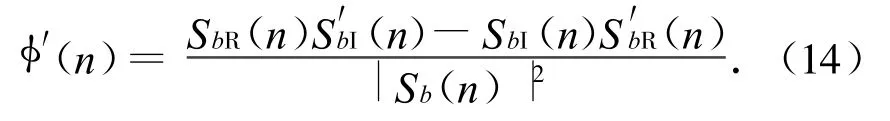
式中：下标R,I分别表示函数的实部和虚部。

因使用了相位的导数,要求原相位函数连续光滑。通过插值合理调整积分步长就可满足

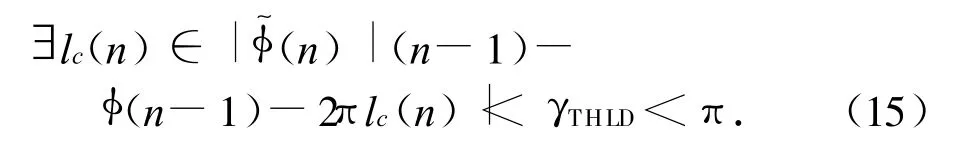
式中：γTHLD为相位中相邻两点的差值。该算法的核心是根据函数变化的快慢自适应地调整步长,在变化剧烈处适当插值缩短步长,相对平滑处增加步长,当误差小于设定的门限(γTHLD)即完成估计,γTHLD的大小取决于应用对精度的要求。此方法最后获得对相位的一致估计,完成相位解缠。

2.2.2 插值与可调门限相结合算法

此算法的核心是先对回波作插值处理,再对插值所得主值相位相邻的两点的值进行判断,当这个差值超过门限时,对后面的相位作2π补偿。算法的判断公式为

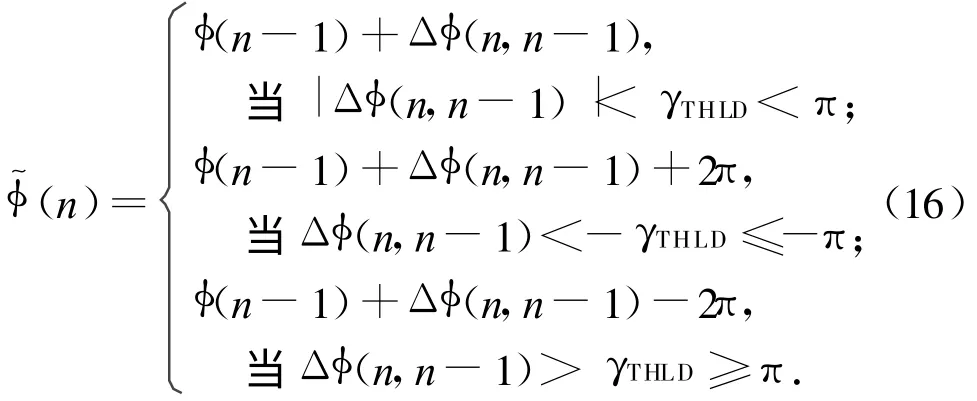
式中：Δφ(n,n-1)为主值相位差,且Δφ(n,n-1)=arg Sb(n)-arg Sb(n-1)。

该算法受采样率的影响较大,采样率不足时应尽量对回波信号进行插值处理,再提取相位主值进行解缠。

3 仿真

设雷达波长0.43 m,雷达发射25.6μs的矩形脉冲,脉冲重复周期0.1 ms,飞机飞行径向速度30 m/s,雷达视角30°,螺旋桨桨叶参数a=0 m,b=1.2 m,f p=50 Hz。N分别为2,4,12时,插值与可调门限相结合算法所得相位解缠结果分别为图5～7所示。由图可知：相位可近似视作有一定间隔的幅度π的脉冲叠加于一条斜线上,与式(9)吻合。桨叶空间位置的对称性使角度相差π的每对桨叶的回波能相干叠加,致使相位出现幅值为π的跳变。由图可得斜线的斜率为-875 rad/s,与由2πfd而得的理论值-876.7 rad/s基本相符。同时,相位呈现一定的螺旋桨周期调制特征,图5每隔9个脉冲为1个周期,0.02 s内共有2个周期,而螺旋桨的调制周期为0.02 s,桨叶数为2;图6每隔6个脉冲为1个周期,桨叶数为4;图7每隔2个脉冲为1个周期,桨叶数为12,表明相位的调制周期为螺旋桨调制周期的1/N。N分别为3,5,15时,自适应数值积分算法所得相位解缠结果分别如图8～10所示。与N为偶数相比,N为奇数时经解缠的相位显更平滑,且周期性更明显,桨叶数越多,相位的波动就越接近正弦波形。螺旋桨调制周期为0.02 s,图8～10的相位的周期分别为螺旋桨调制周期的1/3,1/5,1/15。因此,其周期性质与N为偶数时一致。

图5 用插值与可调门限相结合算法解缠后相位(N=2)Fig.5 Phase after phase-unwrapping achieved by arithmetic of interpolation and adaptive threshold(N=2)

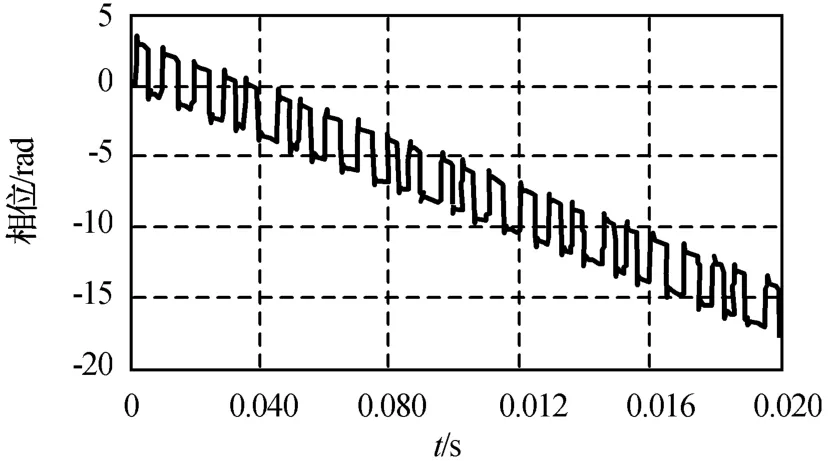
图6 用插值与可调门限相结合算法解缠后相位(N=4)Fig.6 Phase after phase-unwrapping achieved by arithmetic of interpolation and adaptive threshold(N=4)

图7 用插值与可调门限相结合算法解缠后相位(N=12)Fig.7 Phase after phase-unwrapping achieved by arithmetic of interpolation and adaptive threshold(N=12)

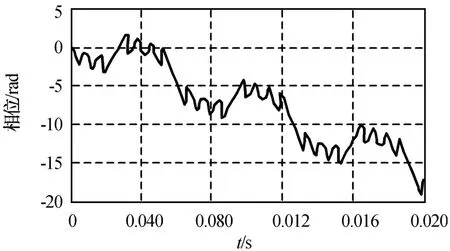
图8 用自适应数值积分算法解缠后相位(N=3)Fig.8 Phase after phase-unwrapping achieved by arithmetic of self-adaptive numerical integration(N=3)

4 结束语

图10 用自适应数值积分算法解缠后相位(N=15)Fig.10 Phaseafter phase-unwrapping achieved by arithmetic of self-adaptive numerical integration(N=15)

本文建立了螺旋桨雷达回波信号的模型,对模型回波信号的相位混叠效应进行了理论分析,推导了桨叶数为偶数时回波模型的改进形式,分析了螺旋桨调制模型中雷达回波的相位理论值。讨论了螺旋桨回波相位出现模糊的原因,并据此提出了插值与可调门限相结合的算法和自适应数值积分算法两种算法分别在桨叶数为奇数和偶数时进行相位解缠,结果较理想,由解缠后相位图对多普勒频率和螺旋桨调制周期估计的精度也较好。对螺旋桨相位的特征的研究可用于目标的识别和分析,是对基于频谱分析的目标识别的重要补充。方法有较好的应用前景。

[1]CHEN V C.Radar signatures of rotor blades[C]//International Society for Optical Engineering.Washington D.C.：SPIE,2001：63-70.

[2]BELL M R,GRUBBS R A.JEM modeling and measurement for radar target identification[J].IEEE Trans.On AES,1993,29(1)：73-87.

[3]MARTIN J,M ULGREW B.Analysis of the theoretical return signal from aircraf t blades[C]//Proceedings of IEEE International Conference on Radar 1990.Washington D.C.：IEEE,1990：569-572.

[4]DING J J,YU Z Q,YAN D Z,et al.Modeling and validation of modulated characteristics for aircraft rotating structure in the air surveillance radars：IEEE International Radar Conference[C].IEEE,2005：641-646.

[5]OPPENHEIM A V,SCHAFER R W.Digital signal processing[M].Englewood Cliffs,NJ：Prentice-Hall,1995.

[6]TRIBOLET J. A new phase unwrapping algorithm[J].IEEE Transactions on Signal Processing,1977,25(2)：170-177.