复合结构装药爆轰波爆速与曲率关系的数值模拟

向 梅,饶国宁,彭金华

(南京理工大学化工学院,江苏 南京 210094)

引 言

随着现代战争的发展,炸药的安全可靠性越来越受到重视。对于钝感弹药装药结构,国内外研究较多,如针对传爆系统的装药结构进行研究[1-3],目的是保证可靠起爆钝感炸药。杨慧群等人[4]对主装药的装药设计进行了研究,从原理上证实改变装药结构可以使炸药具有低易损性。

爆轰波在均匀柱形炸药中传播时,爆速和阵面形状都会进入一种与初始情形无关的状态。曲面爆轰波传播的一个显著特征是爆轰波阵面某点的法向传播速度取决于该点处波阵面的空间平均曲率,Eyring最早从理论和实验中得到了发散爆轰波的爆速亏损公式[5],在此基础上,本研究设计了内外层装药的复合结构,采用数值模拟的手段研究了复合装药结构中曲面爆轰波的爆速和曲率的关系,为研究该结构的低易损性提供理论依据。

1 曲面爆轰波的爆速-曲率关系

研究表明[6],爆轰波阵面某点的法向传播速度Dn和该点处的波阵面空间平均曲率κ的关系是炸药的一种基本爆轰性能,与炸药的几何形状、边界条件和起爆方式基本无关。爆轰波阵面的运动在几何上是由曲率确定的,给定曲率效应关系和边界条件,在数学上就决定了爆轰波阵面传播的几何学或运动学规律,无须依赖于爆轰产物流场的计算。常见的D n-κ的关系有:线性近似关系、不同反应阶数、DSD计算用的关系等[5]。

在Dn-κ线性近似关系理论的基础上,本研究提出了复合装药结构D n-κ的关系为:

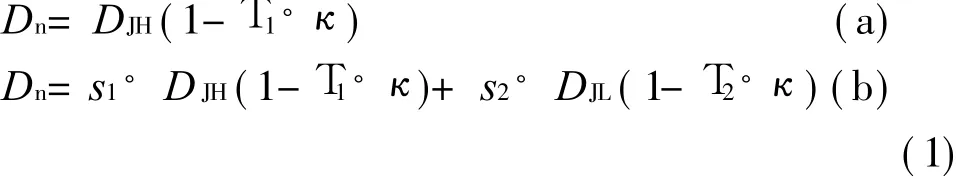
式中:Dn为药柱中的实际爆速;DJH为复合装药结构内部高能炸药的理论爆速;D JL为复合装药结构外部钝感炸药的理论爆速;s1与s2为复合装药结构中钝感炸药和高能炸药相互作用的相关系数;T1和T2分别为内外部炸药与反应区长度和外壳材料性质有关的系数,其值将在完成数值模拟后,利用得到的相关数据进行拟合得到。

如图 1所示,当一定曲率对应的坐标落在PBX9404区域内时 D n-κ的关系用式(1a)描述,落在 PBX9502区域内时用式(1b)表示。

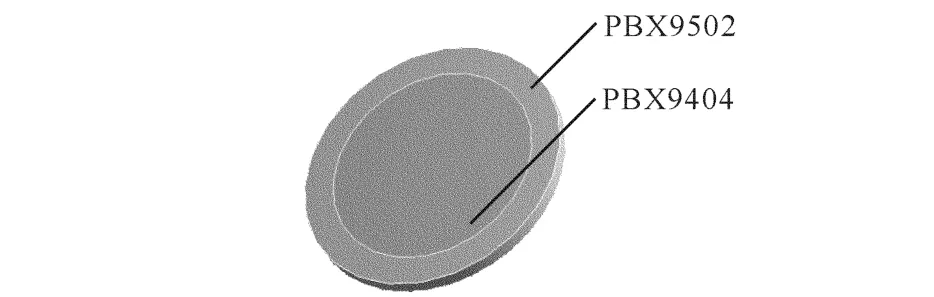
图1 药柱结构示意图Fig.1 The structure of the cylindrical explosive

2 数值模拟

2.1 模拟模型

本研究模型结构及尺寸如图 2所示,该模型为高 1cm的圆柱形药柱,内外层分别为等高的PBX9404和 PBX9502炸药,其中R表示复合装药结构中 PBX9404的半径,d表示外层 PBX9502的厚度。起爆点设置在药柱上端面中心处。

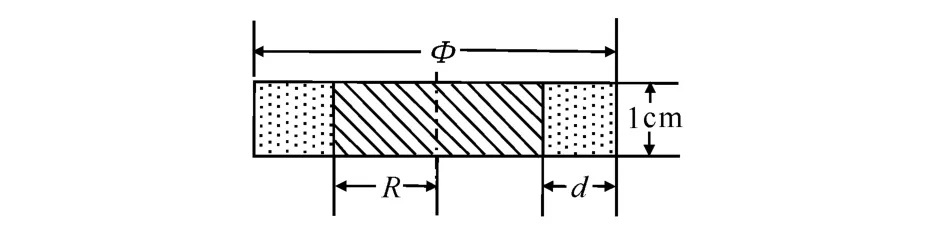
图 2 药柱尺寸及起爆点Fig.2 The dimension of the structure and detonation points

本研究使用 AUTODYN模拟软件。 PBX9404和 PBX9502炸药的状态方程使用 JWL方程[7]:

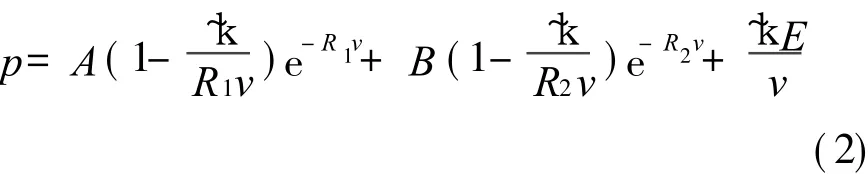
式中:p为爆轰产物的压力;v为爆轰产物的相对比容;E 为比热力学能;A、B、 R1、R2和 k～为状态方程的5个待定参数。两种炸药的爆轰产物 JWL状态方程参数见表 1,均采用 EULER求解器。

表1 炸药爆轰产物 JWL状态方程参数Table 1 JWL equation of state parameters ofdetonation products

在有限元计算方法中,炸药的爆压是用几个单元平滑处理得到的,而爆速与爆压密切相关。故有限元的单元尺度对爆压的大小影响很大,不同的网格划分会得出不同压力和速度,对拟合参数的数值影响也较大。本研究确定尺寸为0.2cm的网格既能满足模拟精度又能避免过大的计算量。

2.2 计算结果

中心单点起爆模拟的目的是为了得到爆速D n与曲率κ的相互关系,选择 3组不同直径的复合结构药柱进行模拟试验,在不同的曲率位置测量爆速,曲率半径增量为 1cm,D n-κ关系曲线模拟结果见表 2。

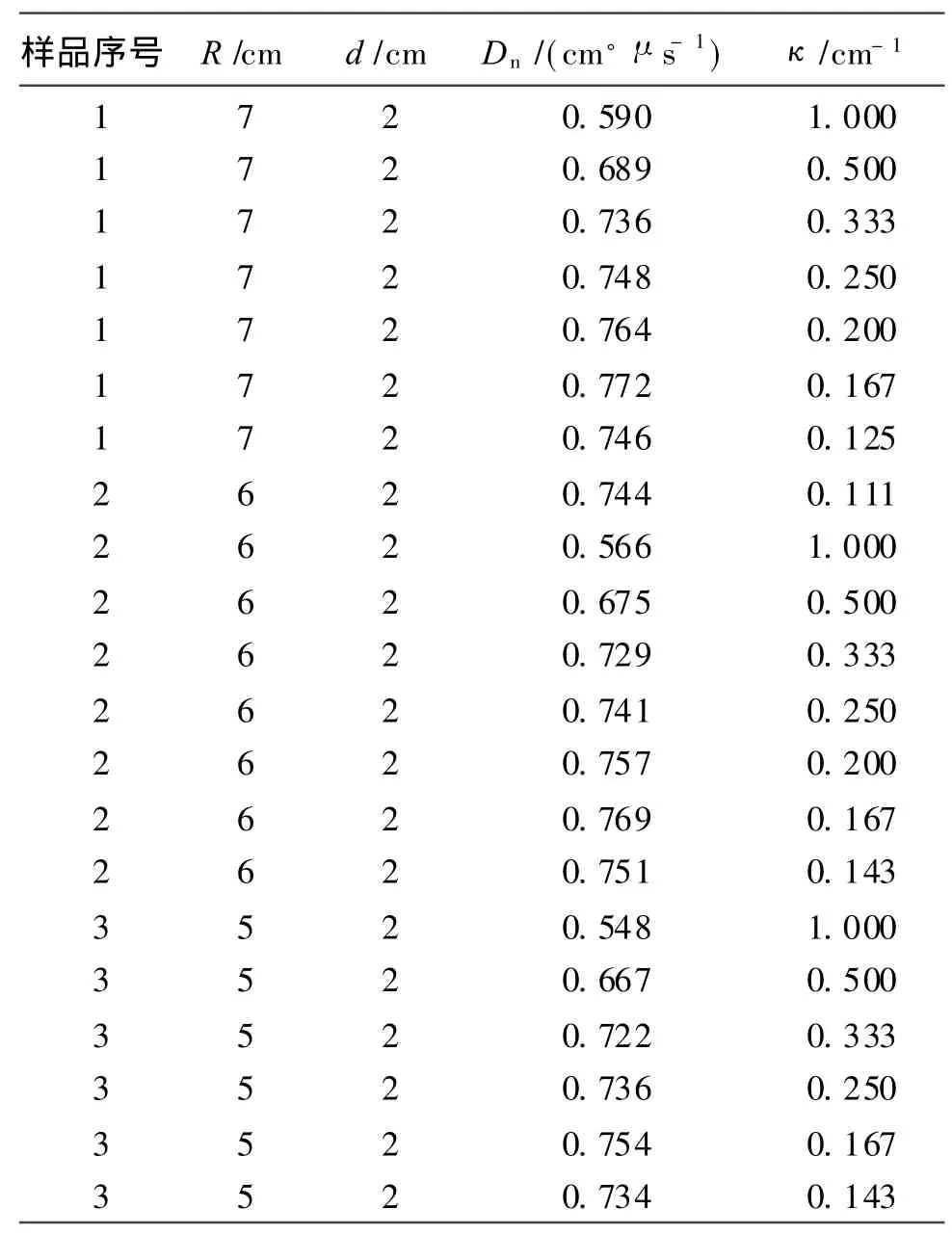
表 2 模拟结果数据表Table 2 Thedata table of simulation results

与文献[8]的研究方法类似,将 3组 D n-κ关系曲线放在同一个坐标系中进行比较分析。如图3所示,虚线右边区域为药柱中 PBX9404部分,左边区域为 PBX9502部分。可以看到,在 PBX 9502区域(外层钝感药部分),随着κ值的增大,爆速变大;在PBX9404区域(药柱中部高能药部分),随着κ值的增大,爆速变小,且不同直径药柱爆速之间的差别逐渐增加,κ值变小,爆速增大;不同尺寸药柱的爆速愈接近于理想爆速,并具有汇聚至一点的趋势。同时,κ一定的情况下,复合结构中PBX9404药柱区域的半径越大,相应测试点的爆速越大;在 PBX9502区域内,曲率相对较小,因此,在不同尺寸药柱内,相应测试点的爆速差别不大,且从图 3可以观察到测试点处的爆速从 PBX9404区域移动到 PBX9502区域时有突变的现象,分析认为这是由两种炸药的爆炸特性不同造成的。

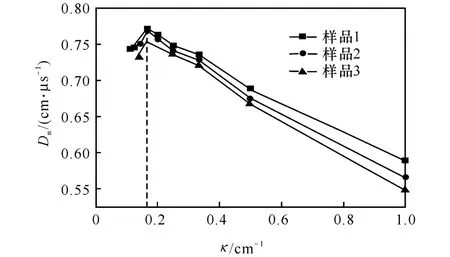
图 3 D n-κ关系曲线Fig.3 The D n-κrelationship

利用模拟得到的样品 1的D n-κ相关参数,对式(1)进行拟合得到近似描述样品 1的爆速-曲率关系式,见式(3),其中钝感区域内的实际爆速是由两种内外层炸药相互作用后得到的:

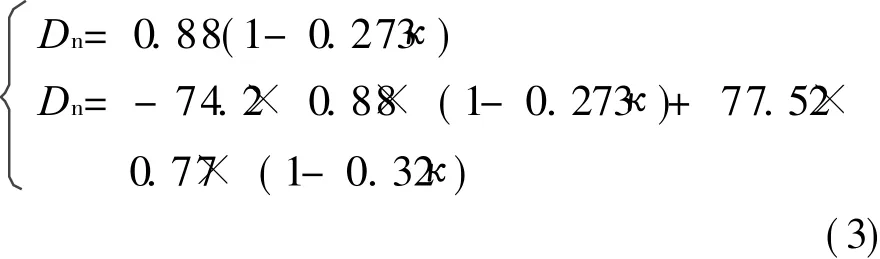
3 结 论

(1)设计并提出了外层钝感、内层高能的装药结构,有限元程序AUTODYN能够较好地应用于该模型的模拟,炸药选用JWL状态方程,EULER求解器,网格尺寸设为 0.2cm既能满足模型的模拟精度,又能避免过大的计算量。

(2)通过研究复合装药结构多个样本的点起爆情形,得到内层为 PBX9404,外层为 PBX9502的复合药柱的爆速D n和曲率κ的关系。

(3)基于曲面爆轰波曲率和爆速的线性近似关系,提出了适合复合装药结构的近似方程,利用模拟得到的数据拟合得到了近似的爆速-曲率关系方程的参数。

[1] 胡双启,曹雄.高起爆能力的新结构传爆药柱研究[J].兵工学报,2002,23(2):166-168.HU Shuang-qi,CAO Xiong.A study on thestructure of booster pellets having high initiating capacity[J].Acta Armamentar,2002,23(2):166-168.

[2] 高桂萍.钝感弹药及安全可靠起爆新技术 [J].火炸药学报,1999(2):65.GAO Gui-ping. Desensitive ammunition and new techniques of safe reliable initiation[J]. Chinese Journal of Explosives and Propellants,1999(2):65.

[3] 张金勇,胡双启 ,曹雄.新结构传爆药柱多点起爆数值模拟及实验研究 [J].工业安全与环保,2006,32(5):37-38.ZHANG Jin-yong,HU Shuang-qi,CAO Xiong.Multi point synchronous initiation numerical simulation on new structure and its experimental study[J]. Industrial Safety and Environmental Protection,2006,32(5):37-38.

[4] 杨慧群,王泽山 ,魏晓安.装药中的不同间隙对炸药爆轰性能的影响[J].含能材料,2005,13(4):214-216.YANG Hui-qun,WANG Ze-shan,WEI Xiao-an.Effect of explosive charge with variable clearance on detonation performance[J]. Chinese Journal of Energetic Materials,2005,13(4):214-216.

[5] 文尚刚.三维爆轰波传播的 LS方法研究 [D].绵阳:中国工程物理研究院,2001.

[6] Gary JS.The effect of curvature on pathological detonations[J].Combustion and Flame,2000,123(1/2):68-81.

[7] 于川,刘文翰 ,李良忠,等.钝感炸药圆筒试验与爆轰产物 JWL状态方程研究[J].高压物理学报,1997,11(3):227-233.YU Chuan,LIU Wen-han,LI Liang-zhong,et al.Studies on cylinder test and JWL equation of state of detonation product for insensitive high explosive[J].Chinese Journal of High Pressure Physics,1997,11(3):227-233.

[8] Hill L G,Bd zil JB,Aslam T D.Front curvature rate stick measurements and detonation shock dynamics calibration for PBX 9502 over a wide temperature range[C]∥ Proc of 11th Symp(Int)on Detonation.Snowmass:[s.n.],1998:1029-1037.