如何用SAS软件正确分析生物医学科研资料 X. 用SAS软件实现嵌套设计和裂区设计定量资料的统计分析

陶丽新，胡良平

如何用SAS软件正确分析生物医学科研资料 X. 用SAS软件实现嵌套设计和裂区设计定量资料的统计分析

陶丽新，胡良平

编者按

生物统计学是生物学领域科学研究和实际工作中必不可少的工具，在分子生物学迅速发展的今天，生物统计学更显示出了它的重要性。实验设计与数据统计分析是现代生物学的基石，是生物学研究者检验假说、寻找模式、建立生物学理论的有利工具，也是生物学研究者探索微观和宏观生物世界的必备基础知识。对于每天甚至是每时每刻涌现的大量的、以天文数字计量的分子遗传数据，必须借助统计学知识加以分析处理，才能从中获得有意义的信息。“生物多样性数据分析”是开展生物多样性研究的一个重要方面，数据分析能力的高低极大地影响着我们对各种生态学现象认识的深度和广度。现在，电子计算机的普及使得生物统计分析过程大大简化，生物统计分析软件包的普及将生物统计学从统计学家的书本里解放了出来，简化了生物统计分析过程，使之成为生物学研究者的常用工具。本刊特邀军事医学科学院生物医学统计学咨询中心主任胡良平教授，以“如何用 SAS 软件正确分析生物医学科研资料”为题，撰写系列统计学讲座，希望该系列讲座能对生物医学科研工作者有所帮助。

1 嵌套设计及其资料的统计分析

1.1 嵌套设计的概念及应用场合

试验中涉及两个或多个试验因素，且依据专业知识可以认为各试验因素对观测指标的影响有主次之分，主要因素各水平下嵌套着次要因素，次要因素各水平下又嵌套着更次要的因素，这样的试验设计称为嵌套设计。此类设计有两种情形：第一种情形是，受试对象本身具有分组再分组的各种分组因素，处理（即最终的试验条件）是各因素各水平的全面组合，且因素之间在专业上有主次之分（如年龄与性别对心室射血时间的影响，性别的影响大于年龄）；第二种情形是，受试对象本身并非具有分组再分组的各种分组因素，处理（即最终的试验条件）不是各因素各水平的全面组合，而是各因素按其隶属关系系统分组，且因素之间在专业上有主次之分（如研究不同代次不同家庭成年男性的身高资料，不同家庭之间的差别大于同一个家庭内部不同代次之间的差别）。

嵌套设计主要应用于试验因素对观测指标的影响有主次之分的试验研究中，试验因素之间的主次关系要有专业依据，不能凭空想象而定[1-2]。嵌套设计的构造方法和列表格式参见例 1。

1.2 嵌套设计定量资料方差分析的 SAS 实现

例 1在4块相同的试验田中考察肥力和小麦品种对小麦产量的影响，并且假定品种和肥力对产量的影响大小顺序为品种 > 肥力，资料如表1所示。试分析小麦品种和肥力对小麦产量的影响有无统计学意义。

分析与 SAS 实现：该资料涉及两个试验因素，分别为品种与肥力，各有3个水平，两因素各水平全面组合，各种组合条件下进行了 4 次独立重复试验；又由于品种与肥力对产量的影响大小顺序为品种 > 肥力，所以该资料为系统分组（或嵌套）设计。

表1 不同小麦品种和肥力对小麦产量（kg/ha）的影响

具体的 SAS 程序如下：

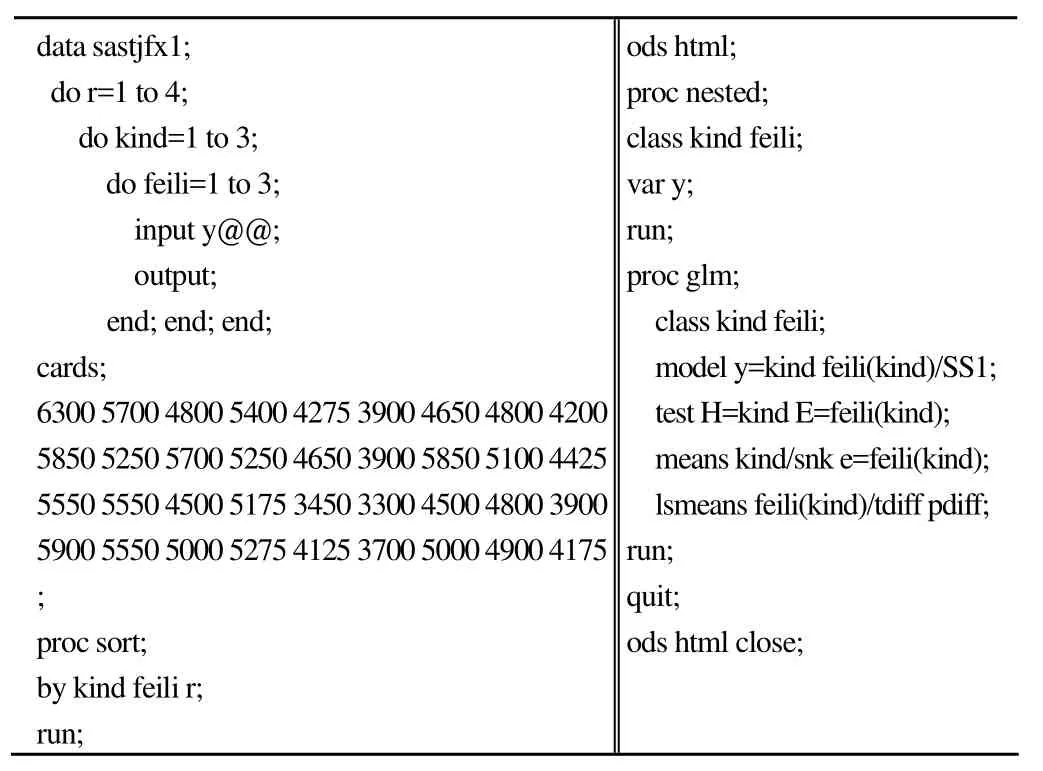
data sastjfx1;do r=1 to 4;do kind=1 to 3;do feili=1 to 3;input y@@;output;end; end; end;cards;6300 5700 4800 5400 4275 3900 4650 4800 4200 5850 5250 5700 5250 4650 3900 5850 5100 4425 5550 5550 4500 5175 3450 3300 4500 4800 3900 5900 5550 5000 5275 4125 3700 5000 4900 4175;proc sort;by kind feili r;run;ods html;proc nested;class kind feili;var y;run;proc glm;class kind feili;model y=kind feili(kind)/SS1;test H=kind E=feili(kind);means kind/snk e=feili(kind);lsmeans feili(kind)/tdiff pdiff;run;quit;ods html close;

作者单位：100850 北京，军事医学科学院生物医学统计学咨询中心

程序说明：数据步建立数据集 sastjfx1，输入变量名和变量值，“r”、“kind”、“feili”、“y”分别代表试验田编号、小麦品种、肥力和小麦产量。sort 过程是对数据集中的变量按照主次重新排序；nested 过程用于对变量已经按照主次排序且来自嵌套设计的平衡资料的方差分析；第 3 个过程为glm 过程，glm 过程的适用面很宽，资料可以是不平衡的，也可以不排序，仅取决于 model 语句和 test 语句的写法，“model y = kind feili (kind)/SS1”表示因素肥力嵌套在品种里，“SS1”表示第 I 型离均差平方和（计算结果与变量在model 语句中的顺序有关），不能选用 SS3；“H = kind E =feili (kind)”表示在考察品种的效应时，以模型中肥力的效应作为误差项。程序中同时使用了 nested 过程和 glm 过程对资料进行分析。

SAS 输出结果与结果解释：

The NESTED procedure

上述结果表明：F = 2.71，P = 0.1453；F = 11.06，P <0.0001，说明就该资料而言，肥力对小麦产量的影响具有统计学意义，但是还没有理由说明小麦品种对小麦产量的影响具有统计学意义。

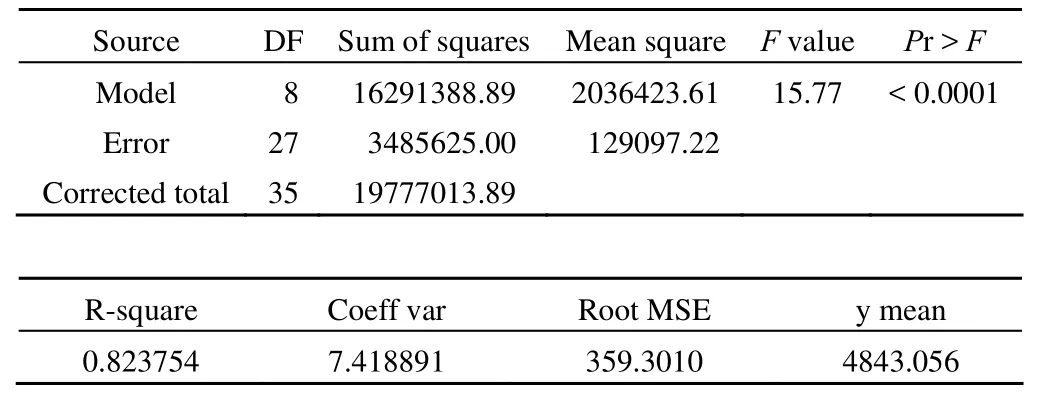
The GLM procedure dependent variable: y

Source DF Type I SS Mean square F value Pr > F Kind 2 7727638.889 3863819.444 29.93 < 0.0001 Feili (kind) 6 8563750.000 1427291.667 11.06 < 0.0001 Tests of hypotheses using the type I MS for feili (kind) as an error term Source DF Type I SS Mean square F value Pr > F Kind 2 7727638.889 3863819.444 2.71 0.1453

上述结果表明：F = 15.77，P < 0.0001，说明总模型具有统计学意义；模型的分项部分只有对肥力分析的结果是正确的，其 F = 11.06，P < 0.0001，说明肥力对小麦产量的影响具有统计学意义；由 test 语句给出的结果，才是对主要因素（小麦品种）的合理检验，其 F = 2.71，P = 0.1453，说明小麦品种对小麦产量的影响没有统计学意义。

Least squares means for effect feili (kind)t for H0: LSMean (i) = LSMean (j) / Pr > |t|Dependent variable: y

以上是 9 种组合情况的小麦产量均值之间两两比较的结果，小麦品种为 A 时，由 t = –3.54241，P = 0.0015 说明高肥与低肥比较小麦产量之间的差别有统计学意义；由t = –1.52521，P = 0.1388 说明高肥与中肥比较小麦产量之间的差别没有统计学意义；由 t = –2.01721，P = 0.0537 说明中肥与低肥比较小麦产量之间的差别没有统计学意义。小麦品种为 B 时，由 t = –4.52642，P = 0.0001 说明高肥与中肥比较小麦产量之间的差别有统计学意义；由 t = –6.19922，P < 0.0001 说明高肥与低肥比较小麦产量之间的差别有统计学意义；由 t = –1.67281，P = 0.1059 说明中肥与低肥比较小麦产量之间的差别没有统计学意义。小麦品种为 C时，由 t = –0.3936，P = 0.6970 说明高肥与中肥比较小麦产量之间的差别没有统计学意义；由 t = –3.24721，P = 0.0031说明高肥与低肥比较小麦产量之间的差别有统计学意义；由t = –2.85361，P = 0.0082 说明中肥与低肥比较小麦产量之间的差别有统计学意义。

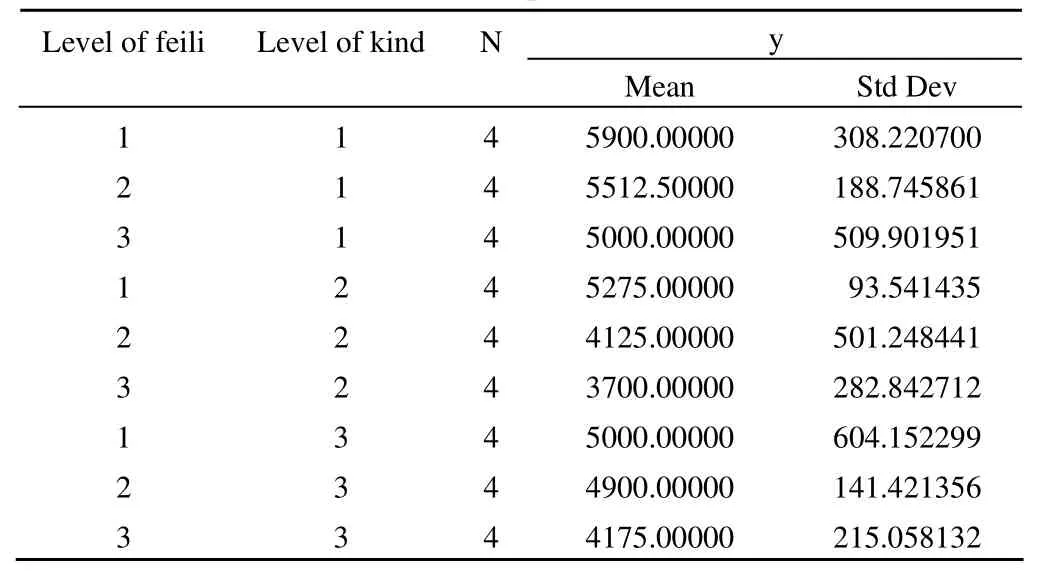
The GLM procedure

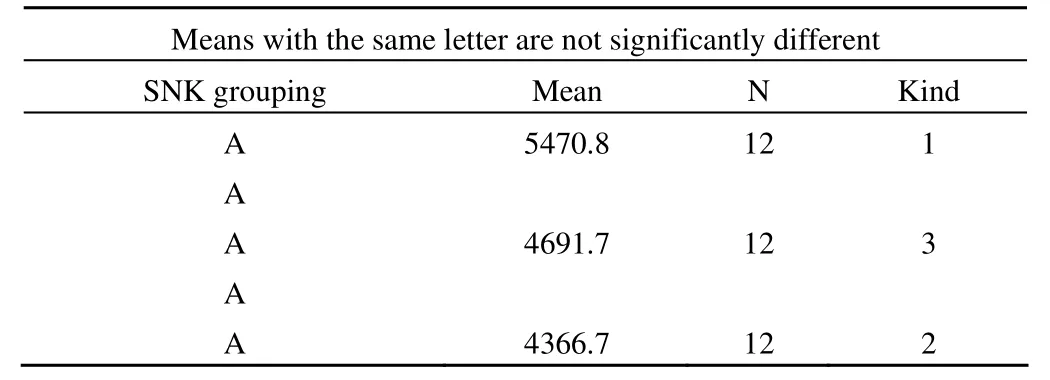
Student-newman-keuls test for y

上述结果表明：不同小麦品种之间小麦产量的差别没有统计学意义。而小麦品种为 A时，高肥的小麦产量高于低肥的小麦产量；小麦品种为 B 时，高肥的小麦产量高于中肥和低肥的小麦产量；小麦品种为 C 时，高肥的小麦产量高于低肥的小麦产量，中肥的小麦产量高于低肥的小麦产量。

2 裂区设计及其资料的统计分析

2.1 裂区设计的概念及应用场合

试验因素分阶段进入试验过程，通常由先进入试验的试验因素（设为 A）构成单因素多水平设计或由先进入试验的试验因素（设为 A）与区组因素（设为 B）构造出含 m次独立重复试验的随机区组设计；再把接受因素 A 各水平处理或接受因素 A 与因素 B 各组合水平处理的 m 个受试对象随机地分配给在第二阶段进入试验的试验因素 C的 m 个水平，这样安排试验因素的方法称为裂区设计或分割设计。

结合实际问题，当试验研究过程自然形成 2 个或多阶段（有时称为工序），各阶段涉及的试验因素彼此不同，但需要等整个试验过程结束后，才能观测定量指标的结果，就需要用到此设计[1-2]。裂区设计的构造方法和列表格式参见例 2。

2.2 裂区设计定量资料方差分析的 SAS 实现

例 2在 3 块不同的试验田中进行玉米的施肥试验。在苗期对每块试验田使用不同的施氮量，即正常施用苗肥（78 kg/hm2）和减少 1/3 苗肥（52.5 kg/hm2）；在 5 叶期，采用灌根法每公顷用清水 600 kg，分别加入不同用量的农夫乐，充分搅拌后，分株剂量浇灌在玉米根部。资料如表2所示。试分析不同的施氮量和不同的农夫乐用量对玉米产量的影响。

表2 不同施氮量和不同农夫乐施用量对玉米产量的影响

分析与 SAS 实现：该资料中，试验因素“不同施氮量”和区组因素在苗期先出现在试验中，每个区组被分成两个一级单位；当玉米生长到 5 叶期时，每个一级单位再被分为3 个二级单位，分别施加 3 种不同用量的农夫乐，定量的观测指标为玉米产量，两个试验因素分两个阶段进入试验过程，所以该资料为裂区（或分割）设计。

具体的 SAS 程序如下：

data sastjfx2;do a=1 to 2;do b=1 to 3;do s=1 to 3;input x @@;output;end;end;end;cards;11.98 11.97 11.93 10.77 10.75 10.75 9.90 9.80 9.60 11.72 11.71 11.70 10.74 10.71 10.73 9.78 9.75 9.76;ods html;proc glm;class a s b;model x=a s a*s b a*b/ss3;test h=a s e=a*s;means a*b;lsmeans a*b/tdiff pdiff;run;quit;ods html close;

程序说明：数据步建立数据集 sastjfx2，输入变量名和变量值，“a”、“b”、“s”、“x”分别代表不同施氮量、农夫乐的不同施用量、试验田编号和玉米产量。过程步调用 glm过程，“test h = a s e = a*s;”表示在分析因素 a 和区组因素s 时，以它们的交互作用的均方作为误差的均方（注意：若出现各组例数不等或某些试验条件下未做试验，应使用 glm过程来实现计算）。

SAS 输出结果与结果解释：

The GLM procedure dependent variable: x

以上结果表明：F = 459.74，P < 0.0001，说明总的模型具有统计学意义。

R-square Coeff var Root MSE x mean 0.998070 0.519693 0.056026 10.78056 Source DF Anova SS Mean square F value Pr > F a 1 0.04013889 0.04013889 12.79 0.0072 s 2 0.01471111 0.00735556 2.34 0.1581 a*s 2 0.00964444 0.00482222 1.54 0.2725 b 2 12.86831111 6.43415556 2049.82 < 0.0001 a*b 2 0.05497778 0.02748889 8.76 0.0097

以上结果表明：对 a * s 的检验，F = 1.54，P = 0.2725，说明不同施氮量与随机区组 s 之间的交互作用没有统计学意义；对 b 的检验，F = 2049.82，P < 0.0001，说明农夫乐不同施用量对玉米产量的影响具有统计学意义；对 a * b 的检验，F = 8.76，P = 0.0097，说明不同的施氮量和农夫乐的不同施用量之间的交互作用具有统计学意义。

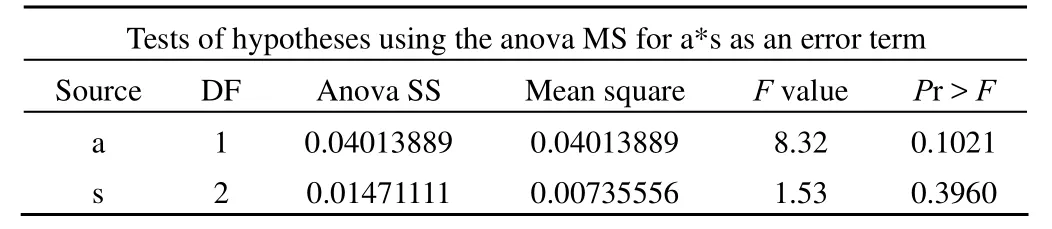
Tests of hypotheses using the anova MS for a*s as an error term Source DF Anova SS Mean square F value Pr > F a 1 0.04013889 0.04013889 8.32 0.1021 s 2 0.01471111 0.00735556 1.53 0.3960

以上结果表明：F = 8.32，P = 0.1021；F = 1.53，P =0.3960，说明不同的施氮量和不同的试验田对玉米产量的影响之间的差别没有统计学意义。

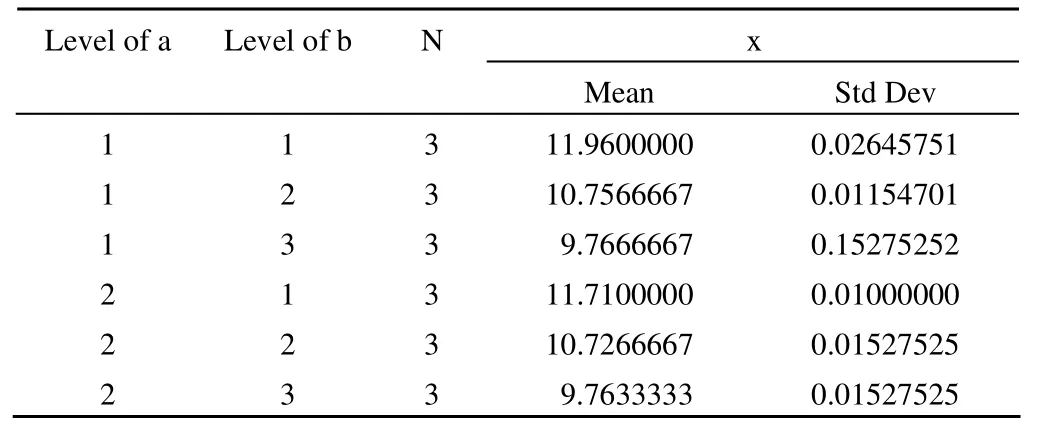
Level of a Level of b N x Mean Std Dev 1 1 3 11.9600000 0.02645751 1 2 3 10.7566667 0.01154701 1 3 3 9.7666667 0.15275252 2 1 3 11.7100000 0.01000000 2 2 3 10.7266667 0.01527525 2 3 3 9.7633333 0.01527525

Least squares means for effect a*b t for H0: LSmean (i) = LSmean (j) / Pr > |t|Dependent variable: x

以上是 6 种组合条件下玉米产量均值之间两两比较的结果。对减肥区而言，由 t = –26.3053，P < 0.0001 说明农夫乐施用量为 30 kg/hm2与农夫乐施用量为 15 kg/hm2之间玉米产量的差别有统计学意义；由 t = –47.9471，P <0.0001 说明农夫乐施用量为 30 kg/hm2与农夫乐施用量为7.5 kg/hm2之间玉米产量的差别有统计学意义；由 t =–21.6418，P < 0.0001 说明农夫乐施用量为 15 kg/hm2与农夫乐施用量为 7.5 kg/hm2之间玉米产量的差别有统计学意义。对正常施肥区而言，由 t = –21.496，P < 0.0001 说明农夫乐施用量为 30 kg/hm2与农夫乐施用量为 15 kg/hm2之间玉米产量的差别有统计学意义；由 t = –42.5549，P <0.0001 说明农夫乐施用量为 30 kg/hm2与农夫乐施用量为7.5 kg/hm2之间玉米产量的差别有统计学意义；由 t =–21.0588，P < 0.0001 说明农夫乐施用量为 15 kg/hm2与农夫乐施用量为 7.5 kg/hm2之间玉米产量的差别有统计学意义。

由以上结果可以看出，减肥区和正常施肥区比较玉米产量之间的差别没有统计学意义；但是无论是减肥区还是正常施肥区，农夫乐施用量的不同造成的玉米产量之间的差别都具有统计学意义，玉米产量的高低顺序为农夫乐施用量30 kg/hm2> 15 kg/hm2> 7.5 kg/hm2。

[1] Hu LP. Application of statistical triple-type theory in the experiment design. Beijing: People’s Military Medical Press, 2006: 85-93. (in Chinese)胡良平. 统计学三型理论在实验设计中的应用. 北京: 人民军医出版社, 2006: 85-93.

[2] Hu LP. The practical course in the statistical analysis for windows SAS, version 6.12 & 8.0. Beijing: Press of Military Medical Sciences,2001:215-222. (in Chinese)胡良平. Windows SAS 6.12 & 8.0实用统计分析教程. 北京: 军事医学科学出版社, 2001: 215-222.

10.3969/cmba.j.issn.1673-713X.2010.04.017

胡良平，Email：lphu812@sina.com