基于直方图的概率数据流聚类算法
2010-09-15程转流胡为成
程转流 胡为成
(铜陵学院,安徽铜陵 244000)
基于直方图的概率数据流聚类算法
程转流 胡为成
(铜陵学院,安徽铜陵 244000)
文章提出一种概率数据流聚类方法PWStream。PWStream采用直方图保存最近数据信息摘要,在允许的误差范围内删除过期的数据元组;并设计了一种基于距离和存在概率的簇选择策略,从而可以发现更多的强簇。理论分析和实验结果表明,该方法具有良好的聚类质量和较快的数据处理能力。
概率数据流;聚类;直方图
数据流就是大量连续到达的、潜在无限的数据的有序序列,对数据流中进行聚类分析已成为数据挖掘的热点之一。最具代表性的数据聚类算法是Aggarwal提出CluStream算法[1],在CluStream算法的基础上,Aggarwal等又提出了专门针对高维连续属性数据流的HPStream算法[2];针对CluStream算法只适应于球形聚类,不能支持任意形状聚类的缺点,Feng Cao等人[3]中提出了针对动态进化数据流的Den Stream算法,它可以进行任意形状的聚类。常建龙等人[4]提出了一种基于滑动窗口的数据流聚类分析算法CluWin。实际上,由于数据产生的随机性、数据收集的不完全性,不确定数据,也即概率数据大量存在于数据流中,这种数据流就是概率数据流[5]。对此,戴东波等人[6]提出一种在概率数据流上进行聚类的有效方法PStream。但P-Stream算法并不适用于滑动窗口模型下的概率数据流聚类分析问题,本文提出一种新的算法PWStream,该算法利用直方图存储最近数据记录的分布状况,并设计出符合概率数据流的簇选择策略和簇合并策略,从而挖掘出概率数据流中存在概率较大的簇。
1.问题定义和描述


2.PWStream算法
2.1 算法的基本框架
下面将给出PWStream算法,该算法是对一个滑动窗口内的概率数据流进行聚类分析。算法可分为两部分,如图1所示:第1~18为在线部分,维护EHCF结构;第19~21为离线聚类。PWStream算法包含三个参数:S为待处理的概率数据流,ε(0<ε<1)为误差参数,NC为EHCF的最大个数,由系统的有效内存来决定。


图1 PWStream算法过程
PWStream算法的在线部分先把概率流中的前q个元组作为簇(EHCF)的中心(第2行),然后对到来的每一个元组v′,根据存在概率和距离远近两个因素,调用Find_cluster算法选择合适的簇(EHCF)(第5行),如果v′可被候选簇吸收(第6、7行),则加入;否则,看簇(EHCF)的总数是否达到最大值NC,若是,则利用find_two_EHCF算法寻找两个合适的簇(EHCF)合并(第9~12行);再由新元组v′单独创建一个簇(EHCF)(第13行);第14行是检测各EHCF中是否含有过期的TCF,若有,就删除;如果EHCF中不包含任何TCF,就删除该EHCF(第16、17行)。算法merge就是采用文献[4]的方法对两个簇(EHCF)进行合并,算法Find_cluster,find_two_EHCF在后面详细说明。
2.2 寻找合适候选簇算法Find_cluster
设某一时刻PWStream算法在线部分维护的簇(EHCF)的集合EC={C1,C2,…,Cn},当一个新元组<ν,p,t>到来时,要在EC中为其找到一个Ci(1≤i≤n)作为候选簇。假设新元组<ν,p,t>与EC中簇Ci中心点的距离为Di,最近的距离为Dmin,对应的簇为Cmin,在文献[1]中,CluStream算法采用的是只单纯考虑距离的选择方法,也就是选择Cmin作为候选簇,但在概率流中,就要考虑距离与存在概率的综合因素。


find_two_EHCF算法按如下规则选取待合并的两个簇:
Rule 1在对lj1,lj2,…,lju依次扫描的过程中,若第一次遇到的lji(1≤i≤u)满足:Cji1和Cji2分别为过渡簇和强簇,合并之后的簇Cji′为强簇,则选取Cji1和Cji2待合并;
Rule 2如果Rule 1不满足,在对lj1,lj2,…,lju依次扫描的过程中,若第一次遇到的lj1(1≤i≤u)满足:Cji1和Cji2都是强簇,则选取Cji1和Cji2待合并;
Rule 3如果Rule 1和Rule 2都不满足,则选取与lmin对应的两个簇Cmin1和Cmin2待合并。
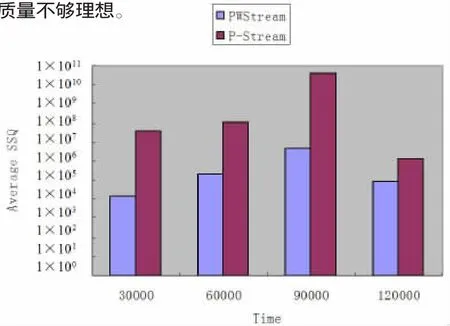
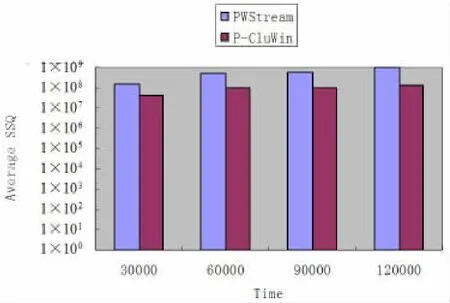
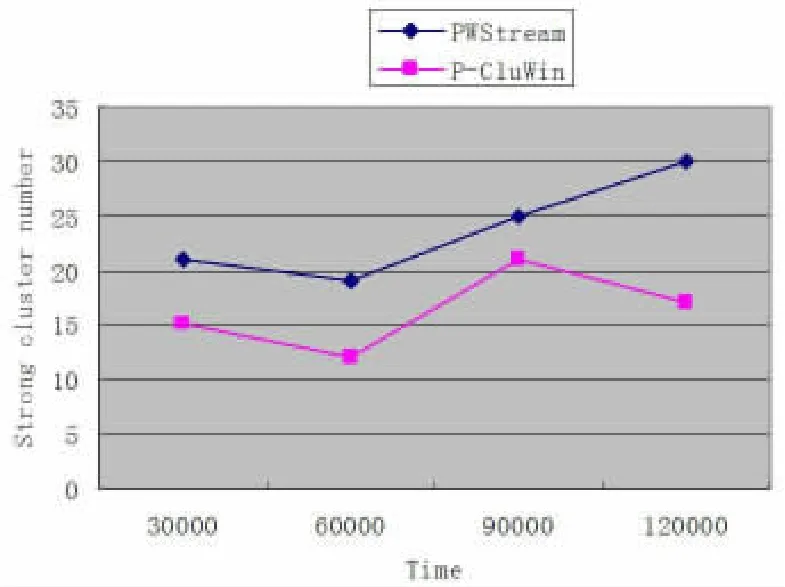
定理1设△SSQ(I)和△SSQ(II)分别表示根据算法CluS-tream选择策略(仅考虑距离因素)和算法find_two_EHCF选择策略选取两个簇(EHCF)进行合并所引起的SSQ值的增量,则有△SSQ(II) 证明:为方便起见,假设概率数据流中的元组ν值是一维的,算法CluStream选择策略(仅考虑距离因素)找到的边为lmin,与之对应的两个簇为Cmin1和Cmin2,元组的个数分别为imin1和imin2,元组值分别为a1,a2,…,aimin1和b1,b2,…,bimin2,中心点分别为Vmin1和Vmin2,合并之后的簇为C′min,中心点为V′min;find_two_EHCF选择策略找到的边为lk,与之对应的两个簇为Ck1和Ck2,元组的个数分别为ik1和ik2,中心点分别为Vk1和Vk2,合并之后的簇为C′k,中心点为V′k,则 很显然,上述两个算法在选取待处理的簇时,均考虑了距离和存在概率两个因素,在距离允许的情况下(用参数M1,M2来约束),尽量提高待处理簇的存在概率,这样在最终离线聚类时的强簇数量就较多,又因为M1,M2的存在,总的距离平方和SSQ不会提高很多。 3.1 实验设置 所有实验都在2.79GHz的PC上进行,操作系统为Windows XP,算法用VC++实现。我们用文献[4]的CluWin算法、文献[6]的P-Stream算法与PWStream算法进行比较。因为CluWin算法主要是针对确定数据流的,而PWStream是针对概率数据流的,为了便于比较实验结果,我们将PWStream算法中采用CluWin算法中选择候选簇(EHCF)策略和选择两个等合并簇(EHCF)策略的算法称为P-CluWin算法,从而将PWStream算法与P-CluWin算法进行比较。 实现数据包括真实数据集和人工数据集,存在概率采用在[θ,1]上均匀分布的数据。 图4 PWStream与P-Stream的SSQ比较 图2 PWStream与P-CluWin的SSQ比较 图3 PWStream与P-CluWin的强簇数据比较 真实数据集采用KDD-CUP′99和KDD-CUP′98两个数据集。人工数据集满足一系列高斯分布。每10K个数据点改变一次当前高斯分布的中心和方差,且采用如下标记描述人工数据集:‘B’表示数据集中包含的数据点数;‘C’表示簇的个数;‘D’表示数据点的维数。例如,B100C20D30表示数据集包含100K个数据点,分别属于20个不同的簇,各数据点的维数为30。 在实验中,PWStream中的EHCF最大个数与P-CluWin算法的EHCF最大个数、P-Stream中的最大微簇个数相等。除非特别指明,PWStream算法中的各参数设置如下:θ=0.05,ε= 0.1,N=10000。 3.2 聚类质量 聚类质量评价标准采用SSQ和强簇数目,由于最能影响聚类质量的是:(1)新元组到来时,选择候选簇的策略;(2)当簇(EHCF)的个数达最大值时,选择两个簇进行合并的策略。我们分别比较算法PWStream与P-CluWin、P-Stream在数据集KDD-CUP′98和KDD-CUP′99的实验结果。为了保证结果更准确,算法采用不同的α,β,M1和M2值各执行5次,并计算平均SSQ和平均强簇数目作为结果值。 PWStream与P-CluWin的聚类质量比较如图2和图3所示(KDD-CUP'98数据集)。由于β的平均值为0.2,θ=0.05,M1的平均值为5,M2的平均值为10,从图2中可以看出,如定理2和定理3所言,PWStream的SSQ不会超过P-CluWin的10倍,但在每个时标处,从图3所示,PWStream找到的强簇都比P-CluWin的要多,如在时标120000处,强簇个数的差别最大。并且PWStream找到强簇个数主要是呈增长趋势,而PCluWin找到的强簇个数不稳定。这主要得益于PWStream算法中的候选规则,在M1和M2不是很小的情况下,PWStream以应用Rule 1和Rule 2为主来找到候选簇和待合并的两个候选簇,而这两条规则用以保持强簇个数不变或增大。而PCluWin只考虑了最近距离而没有考虑簇的存在概率,致使强簇个数不稳定。 PWStream与P-Stream的聚类质量比较如图4所示(KDD-CUP’99数据集)。由于PWStream与P-Stream都是对概率数据流进行聚类,所采用的候选簇(EHCF)策略类似,所不同的是PWStream是在滑动窗口内进行聚类,忽略过期元组,而P-Stream是对所有元组进行聚类,两者所得到的强簇数量差不多,但从图4可看出,两者在SSQ上相差较大,PWStream高质量的聚类结果主要是因为EHCF结构能够准确捕获当前记录的分布状况,旧记录在在线聚类过程中被及时地删除,当EHCF在簇中心发生偏移时,能保持一个较小的半径,然而在P-Stream中,微簇内各记录的时标被累加起来,当簇中心发生漂移时,微簇半径将不断增大,这将混淆不同的簇,并导致聚类质量不够理想。 本文提出一种基于滑动窗口的概率数据流聚类算法PWStream,该算法采用聚类特征指数直方图作为概要结构,可较好地保存数据流当前窗口内的数据分布状况,从而获取较高质量的聚类效果;并且(1)新元组到来时,选择基于距离和存在概率的新候选簇的策略,(2)当簇(EHCF)的个数达最大值时,基于距离和存在概率选择两个簇进行合并的策略,能找到更多的强簇,但其SSQ不会超过仅根据距离选择策略的常数倍。实验结果表明,在概率数据流中,P-Stream算法相对于传统方法有较好的聚类质量,能够有效地适应数据流的演化情况。 [1]Aggarwal C C,Han Jia-Wei,Wang Jian-Yong,Yu P S.A framework for clustering evolving data streams[R].Proceeding of the 29th International Conference on Very Large Data Bases,Berlin,Germany,2003:81-92. [2]Aggarwal C C,Han Jia wei,Wang Jian-yong,Yu P S.A framework for projected clustering of high dimensional data streams [R].Proceedings of the 30th International Conference on Very Large Data Bases,Toronto,Canada,2004:852-863. [3]Cao Feng,Ester M,Qian Wei-Ning,ZhouAo-Ying.Densitybased clustering over an evolving data stream with noise[R]. Proceedings of the 6th SIAM International Conference on Data Mining,Bethesda,MD,USA,2006:326-337. [4]常建龙,曹锋,周傲英.基于滑动窗口的进化数据流聚类[J].软件学报,2007,18(4):905-918. [5]Cormode G,Garofalakis M.Sketching probabilistic data streams. In:Chan CY,Ooi BC,Zhou A,eds[C].Proc.of the ACM SIGMOD Int'1 Conf.on Management of Data,Beijing:ACM Press,2007. 281-292. [6]戴东波,赵杠,孙圣力.基于概率数据流的有效聚类算法[J].软件学报,2009,20(5):1313~1328. TP311 :A :1672-0547(2010)02-0073-03 2010-03-04 程转流(1979-),女,安徽潜山人,铜陵学院数学与计算机科学系讲师,硕士,研究方向:数据流挖掘、多Agent系统; 胡为成(1975-),男,安徽桐城人,铜陵学院数学与计算机科学系副教授,硕士,研究方向:数据流挖掘、遗传程序设计等。 安徽省高等学校自然科学研究项目(编号:KJ2009B139);安徽省高等学校青年教师科研资助计划项目(编号:2008jq1143)。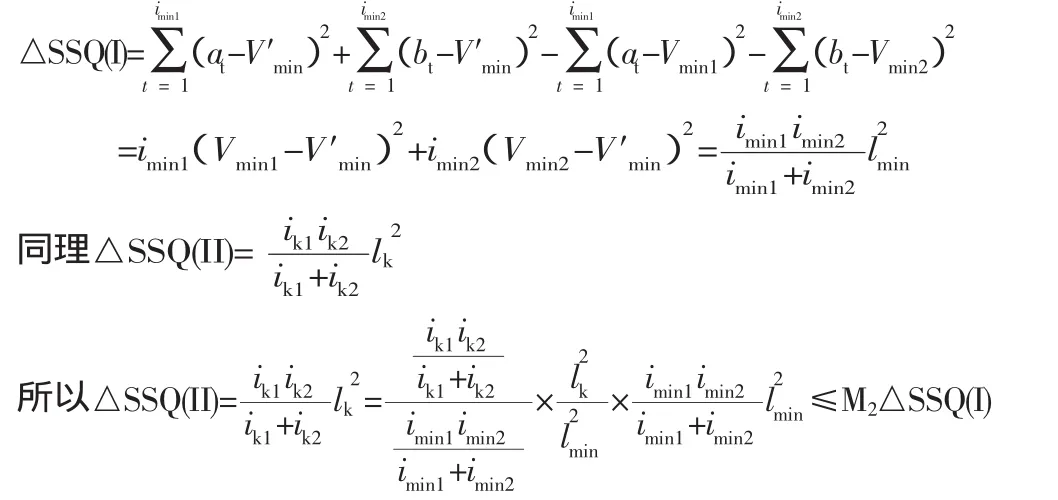
3.实验结果和分析
4.结束语
