BP 算法应用中的关键问题
2010-09-15陶保壮方厚加
陶保壮,方厚加
(淮南联合大学计算机系,安徽淮南232001)
BP 算法应用中的关键问题
陶保壮,方厚加
(淮南联合大学计算机系,安徽淮南232001)
分析了学习方法的选择、隐层数和隐层单元、学习步长的选择、避免局部最小的方法、学习样本的选择、激活函数的选择等使用BP算法时应考虑的问题,并将BP网络应用于化学反应催化模型。
BP算法;隐层数和隐层单元数;学习步长;学习样本
BP算法的基本思想是,学习过程由信号的正向传播与误差的反向传播两个过程组成[1](P42)。正向传播时,输入样本从输入层传入,经各隐层逐层处理后,传向输出层。如果输出层的实际输出与期望的输出不符,则转入误差的反向传播阶段。误差反传是将输出误差以某种形式通过隐层向输入层反传,并将误差分摊给各层的所有单元,从而获得各层单元的误差信号,此误差即作为修正单元权值的依据。这种信号正传播与误差反向传播的各层权值调整过程,是周而复始地进行的。权值不断调整的过程,也就是网络的学习训练过程。该过程一直进行到网络输出的误差减小到可接收的程度,或者进行到预先设定的学习次数为止。
1 BP算法应用中的问题
1.1 学习方法的选择
1、单样本学习法根据每一个学习样本的误差,求权值修正值,更新值;成批学习法根据所有学习样本的总误差,求权值修正值,更新权值。一般来说,学习样本中噪声较小时,用单样本学习法较合适。
2、单样本学习法的缺点是每次迭代的梯度值受学习样本中的噪声影响较大,而成批学习法的缺点是忽略了学习样本的个体差异而降低学习的灵敏度。通常,可以将上述两种方法进行折衷,即将学习样本集分成若干个子块分别进行以子块为单位的成批学习,当误差收敛到一预定数值,再以此时权值为初值,转入下一个子块进行学习,在所有的子块学习完后,如果总的误差满足要求,学习结束。否则,转入下一个循环继续学习。
3、规模较大的BP网络学习时,可以将它以一定的比例缩小成较小的BP网络,先训练这个较小的BP网络,将学习的结果以同样的比例提升到原来较大规模的网络,再训练较大规模的网络。实验证明对于大规模BP网络这种学习方法速度快,特征抽取能力强[2](P65-69)。
1.2 隐层数和隐层单元数的选择
1、一般总是先选择一个隐层的BP网络,但如果选择一个隐层时,隐层单元数目较大,可以考虑选用两个隐层,而每个隐层的单元数取较小值。
2、隐层单元数目HN的选择是否合适是应用BP网络成功与失败的关键因素之一,HN值太小,学习过程可能不收敛;HN值越大,网络映射能力越强,局部最小点越少,越容易收敛到全局最小点[3]。但HN过大,不但使学习时间过长,而且网络容易训练过度,会使网络的容错性降低。因为如果网络对学习样本的学习太“精确”,即使检测样本与学习样本之间有很小的畸变,网络也会判为非。目前,最佳隐层单元数的选择尚无理论指导。实际应用中,可以先取较小的HN,训练并检验网络的性能。然后稍增大HN,再重试。试验确定合适的[3]。
1.3 学习步长的选择
学习步长(或称学习速率)的取值较大时,学习速度快,但会引起权值振荡,太大将引起权值发散;取值较小时,网络学习速度慢,训练时间长。步长的取值应在学习速度与权值的稳定性之间折衷选择,但最好是用变步长的方法。文献[2]给出一种方法,先设一初始步长,若一次迭代后误差增大,则将步长乘以小于1的正数,否则步长乘以大于1的正数。步长随学习的进展而逐步减小。文献[3]根据连续两次迭代时,梯度方向的相似或相反,来增加或减小步长。应该注意的是,学习步长的选择与的动量因子的选择不是孤立的,它们之间有一定的等效性。
1.4 避免局部最小的方法①
1、增加动量项(或称惯性项、矩项等)并适当选择动量因子(或称惯性系数),可以抑制学习过程中的振荡和有助于摆脱局部最小。动量因子一般选在0.9左右。根据连续两次迭代时,梯度方向的相似或相反,来增加或减小动量因子(与学习步长同时考虑)。
2、给权值加小的随机扰动,有助于网络摆脱局部最小。
3、将BP算法与模拟退火算法或遗传算法结合起来,可以避免陷入局部最小,但要影响学习速度。
1.5 学习样本的选择
1、选择学习样本时,不仅要包括所有的模式类别,而且每种类别所具有的学习样本数要平衡,不能偏重某一类型。但如果事先明确类型A出现的机会比类型B大一倍,这时可以选择类型A的学习样本比类型B的学习样本多一倍。如果事先知道类型A的误差比类型B的大,那么类型A的学习样本要多于类型B的。这样可以改善网络的性能。
2、学习时,在学习样本中适当加些噪声,可以提高网络的抗噪声能力。
3、学习样本应尽可能相互独立而没有相关关系,尽可能用正交设计方法来获得足够多的学习样本。
其它技巧①
1、初始权值最好设置为较小(单极S型函数时,可选-0.3~0.3之间的随机数)。
2、激活函数采用单极S型函数时,学习样本期望输出设置为0.1或0.9较合适。
3、给定一定的允许误差,当网络的输出与样本之间的差小于给定的允许误差时,则停止学习。对网络学习采取这种宽容的做法,可加快学习速度。还可以在开始学习时允许误差取大些,以后逐渐减小。
2 BP网络应用
应用BP网络分析测试了化学反应催化问题,牛顿已给出了化学反应催化问题的说明,其描述如下:
2.1 基于BP算法的多层感知器的模型[4](P127-156)
该模型包含3层:输入层,隐层,输出3层感知器,输入向量为X=(x1,x2,…,xi,…,xn)T,隐层输出向量为Y=(y1,y2,yi,…,ym)T,输出层输出向量为O=(O1,O2,…,Oi,…,Ol)T;期望输出向量为O=(O1,O2,…,Ok,…,Ol)T。
2.2 BP算法的程序实现[5](P109-131)
(1)初始化
初始化权值,权值用一个三维数组表示,W[i][j][k],i表示第几层的权值,j和k分别表示本层节点k和上一层的节点j。
(2)输入训练样本对,计算各层输出u[i][j],其中u[i][j]表示第i层的第j个节点的输出,i从1开始。
(3)计算网络输出误差
e[2][node]=u[2][node]-OutputDate[node],其中数组e表示误差,OutputDate为期望的输出值。
(4)计算各层误差信号
(5)调整各层权值
w[layer][j][i]=w[layer][j][i]+ALPHA*delta_w[layer][j][i]-STUDY_SPEED*g[layer][j][i],其中ALPHA为冲动系数,delta_w[layer][j][i]为冲动向量,STUDY_SPEED为学习速率。g[layer][j][i]是误差函数对权值w的导数。
(6)检查网络总误差是否达到进度要求
判断w ucha>EP是否成立(w ucha为实际输出与期望输出的差,EP是给定值),如果成立,训练结束,否则返回步骤(2)。
2.3 BP网络图[1](P42)
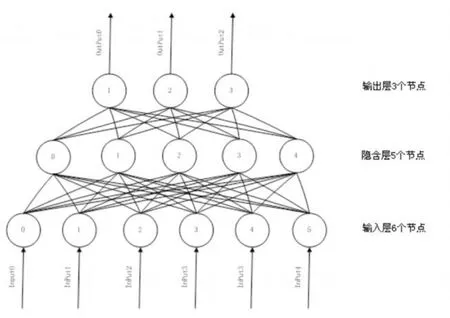
2.4 测试结果
为更好地分析BP算法的实时性、预测精度、收敛性等性能,笔者借鉴引用文献[6]中的相关数据,利用25个边坡实例,对BP神经网络模型进行有效性检验。表1为训练样本,对表中数据进行归一化处理,误差的收敛值为0.001;表中前面数据为催化剂配方比,后三项数据是三种化合物产量比。
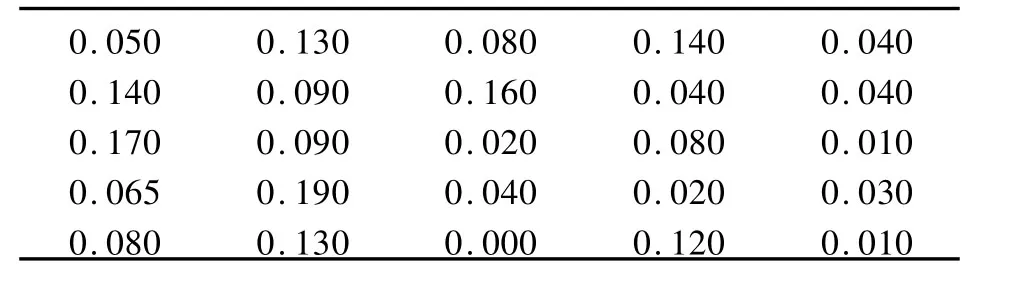
表1 输入数据
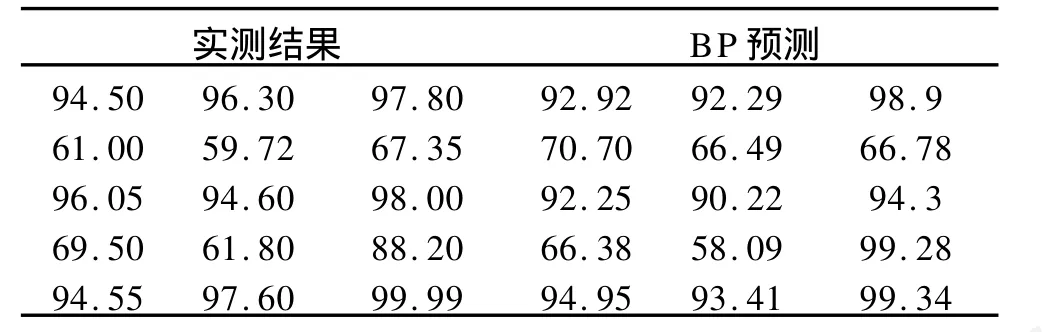
表2 不同催化剂配方实际输出结果与预测结果比较
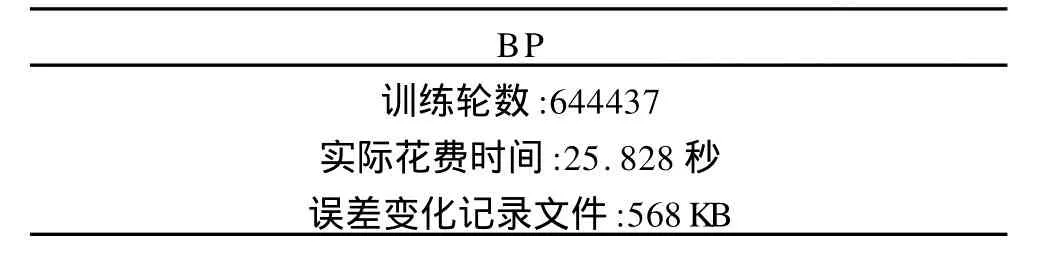
表3 算法性能
2.5 实验分析
BP网络是非线性多层向前网络,对于任一个BP网络,总存在一个感知器(如 RBF)与之对应,反之亦然。BP网络算法采用基于误差反向传播的梯度算法,充分利用了多层前向网络的结构优势,在正反向传播过程中每一层的计算都是并行的,算法在理论上比较成熟;上述实验表明了BP网络的特性主要体现在以下几个方面:
①BP网络的隐层可以是一层或多层。
②BP感知器的隐层和输出层其神经元模型是相同的。
③BP网络的隐单元激励函数计算的是输入单元和连接权值的内积。
⑥BP网络相对于其它网络而言(如RBF)其精确度高、泛化能力较强。
⑦BP网络能以任意精度逼近任何非线性函数,在函数逼近问题上,若样本是非线性的,BP网络效果明显优与其他网络。
⑧BP隐含层难设计,BP网络使用的Sigmoid函数具有全局特性,它在输入值的很大范围内每个节点都对输出值产生影响,并且激励函数在输入值的很大范围内相互重叠,因而相互影响,故BP网络训练过程很长[7]。
3 总结
在实际使用中,由于BP算法的固有特性,BP网络容易陷入局部极小的问题不可能从根本上避免,并且BP网络隐层节点数目的确定依赖于经验和试凑,很难得到最优网络。如上分析,我们可以采用多种方法提高BP网络的性能:如增加学习的样本空间,已知的样本空间越多,提供的客观信息越多,因而训练出的连接权值可以提高预测的准确性;隐层数和隐层单元数的选择要适当,需要通过多次测试给出最优设计,有必要时增加隐含层层数;学习步长应该根据实际情况给出,太小没有区分度,太大则会影响预测效果。
注释:
①张燕萍:《神经网络讲义》,合肥:安徽大学,2007.
[1]张立明.人工神经网络的模型及其应用[M].上海:复旦大学出版社,1993.
[2]黄风岗,宋克呜.模式识别[M].哈尔滨:哈尔滨工程大学出版社,1998.
[3]杨万山,陈松乔,唐连章.基于BP神经网络的工程图纸图形符号识别[J].微型电脑应用,2000,16(2):22-23.
[4]韩力群.人工神经网络教程[M].北京:北京邮电大学出版社,2006.
[5]舒怀林.PID神经元网络及其控制系统[M].北京:国防工业出版社,2006.
[6]孙丽英,葛超,朱艺.RBF神经网络在函数逼近领域内的研究[J].计算机与数字工程,2007,(8):47-48.
[7]潘登,郑应平,徐立鸿,等.基于RBF神经网络的网格数据聚类方法[J].计算机应用,2007,(2):25-27.
The Key Problem of BP Algorithm Application
TAO Bao-zhuang,FANG Hou-jia
(Department of Com puter,H uainan Unit University,H uainan 232001,China)
In this paper the use of BP algorithm should take into account the p roblems and techniques,in particular the choice of learning methods,hidden layers and hidden units,learning step the choice of method to avoid localminimum,the choice of learning samp les,the activation havemade the choiceof function in detail,and then test the app lication of BP netwo rk analysisof the chemical reaction catalyzed model.
BP algo rithm;hidden layer and hidden layer units;learning step;the study sample
TP301.6
A
1009-9735(2010)05-0039-03
2010-07-12
陶保壮(1972-),男,安徽淮南人,讲师,硕士,研究方向:嵌入式系统开发与应用;方厚加(1972-),男,安徽淮南人,讲师,研究方向:数据通信与计算机网络。
