GARCH模型的蒙特卡罗模拟方法及应用
2010-09-15刘旭彬
刘旭彬
(暨南大学 经济学院统计学系,广州 510632)
GARCH模型的蒙特卡罗模拟方法及应用
刘旭彬
(暨南大学 经济学院统计学系,广州 510632)
文章以长江电力(600900)股票和长电CWB1(580007)权证为例进行了实证研究分析,结合GARCH模型与蒙特卡罗模拟方法,利用Eviews和R语言对长电CWB1权证进行了数值方法的定价。实证结果显示出了金融时间序列的GARCH模型特性,并且蒙特卡罗方法定价与实际价格偏差较小,证实了该方法在期权定价中的有效性。
GARCH模型;蒙特卡罗方法;期权定价
0 引言
在众多的金融衍生物当中,期权是一种重要的基础性衍生产品,如何准确地为期权定价一直是众多学者研究的重要课题。
期权定价的经典模型是Black-Scholes模型,该模型需要先估计标的股票收益的波动率,一般采取历史波动率法,但是完全市场与波动率固定不变的假设与实际市场并不完全相符,大量的实证分析证实了Black-Scholes模型定价的偏差。应用GARCH模型对标的股票收益的波动率的时滞性进行探讨,并在此基础上对期权定价问题进行研究,国内外的学者在这方面都有一定的贡献。
Duan[1]运用均衡定价原理通过引入更一般化的风险中性定价关系或叫做局部风险中性定价关系解决了这一难题,从而第一次给出了系统的GARCH期权定价理论。此后,Duan和Simonato[2]结合GARCH模型与马尔科夫链对美式期权的定价问题进行了研究;Duan和Zhang[3]运用GARCH模型研究了香港恒生指数期权的定价问题,研究表明基于GARCH模型的期权定价方法具有较高的准确性。汪来喜、丁日佳[4]应用GARCH模型估计标的股票收益的波动率,并将估计出来的收益波动率代入Black-Scholes期权定价公式,与基于历史波动率下的定价进行比较,结果发现GARCH定价并非总具有优势。王健、李超杰、何建敏[5]基于GARCH-扩散过程,把规范的Black-Scholes期权定价模型推广到存在交易成本的情形,并与Leland的期权定价模型进行了比较。结果表明,有交易成本的GARCH-扩散期权定价模型具有较好的定价性能。张敏、王键[6]研究了期权的数值分析法—Monte Carlo模拟法,为期权的定价提供了估值的数值计算方法。
国内常见的蒙特卡罗模拟方法是假定标的资产价格服从一个几何布朗运动,即根据标的资产价格呈对数正态分布的假设,模拟出资产在期权持有期内的价格走势,得出资产在期权到期日的不同价格分布。上述方法中测度的波动率多为常数,未能如实地反映出金融时间序列波动率的时变性和聚类性。对于如何才能利用可充分反映金融时间序列特有性质的方法来进行期权定价,国内少有相关文献研究。针对以上问题,本文假设股票价格收益率服从一个GARCH类模型,此类模型为准确描述和预测波动率提供了条件,而使用结合了GARCH类模型的蒙特卡罗模拟方法为长电CWB1权证的价格进行数值定价,精确性较高,与实际的偏差较小,证实了该方法定价的有效性。
1 理论依据与技术实现
1.1 GARCH模型
金融时间序列的一个显著特点是条件异方差性。Engel提出自回归条件异方差(ARCH)模型,Bollerslev将其推广到广义ARCH 模型(GARCH)。这些模型以线性形式刻画了误差项的条件二阶矩性质,通过条件异方差的变化来刻画波动的时间可变性及集簇性,GARCH族模型现在已广泛地应用于计量金融领域。对对数收益率rt,我们假定其均值方程是一个ARMA模型,设at=rt-μt使均值修正的对数收益率,考虑如下模型[7]:


1.2 蒙特卡罗模拟方法的理论依据
衍生证券的数值方法通常有二叉树方法,有限差分方法和蒙特卡罗模拟方法。
蒙特卡罗方法是以概率统计的理论和方法为基础的一种计算方法。蒙特卡罗方法将所求解的问题与某个概率模型联系起来,在计算机上进行随机模拟,从而得出问题的近似解,因此蒙特卡罗方法也被称为随机模拟法或者统计试验法。
蒙特卡罗模拟方法的理论依据是风险中性定价。我们考虑一种欧式衍生证券,这种衍生证券的持有者在其有效期内不能做任何决策,假设在T时刻时该衍生证券的收益为fT,那么在风险中性的世界里,其0时刻的价值为:

如果衍生证券只依附一个标的随机变量,并且这个变量不是利率,我们就可以模拟风险中性世界中该标的变量的一种可能路径,然后计算出在这条可能路径下所得到的回报,得到了衍生证券的最终价值,这一最终价值可被看作是全部可能终值集合中的一个随机样本。再选取该变量的第二条样本路径,可以按照上述方法获得第二个样本的终值。更多的样本路径得出更多的样本终值。计算出大量的样本终值后,(fT)就用它们的算术平均值来估计,通过无风险利率对(fT)进行贴现,就可以计算出衍生证券现值的估计值。上述的模拟被称为其中的一次模拟运算。蒙特卡罗方法需要非常大量的模拟运算。
1.3 基于GARCH模型蒙特卡罗模拟方法的技术实现
股票价格t时期的波功率σt可由GARCH(1,1)模型估计出,假设股票的收益率满足如下的形式:
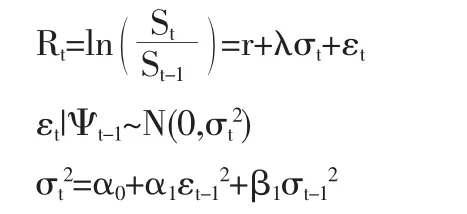
其中{St}为股票每日的收盘价格序列,{Rt}为股票的收益率序列,λ表示单位风险费用 (即市场中的预期风险增加一单位时,收益率就会相应增加λ个单位),Ψt-1表示t-1时刻所有的信息集。
在风险中性的世界中,令 ξt=λσt+εt,则上述模型变为如下形式:

接着运用蒙特卡罗方法对标的股票价格走势进行模拟,其技术实现步骤如下:
(1)创建一个j行k列的标准正态随机矩阵,k表示距离到期时刻T的天数(距到期日时间不包括周末和假期),j表示模拟的路径总数,不妨设j=10000,n(j,k)表示标准正态随机矩阵中的一个元素。
(2)创建一个波动率矩阵σ(j,k),该矩阵第一列的元素可用历史波动率的方法估计α0,α1,β1可以用Eviews软件估计出,ξ(j,k)=σ2(j,k)n(j,k),代入波动方程可得到波动率矩阵。
(3)模拟股票价格的走势,到期日T的股票价格ST的计算方法如下:
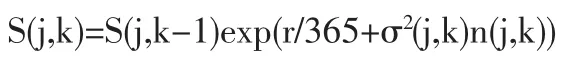

图1 长江电力日收益率波动的波动

图2 长江电力日收益率的频数图及统计特征
(4)则欧式看涨期权在GARCH(1,1)模型下的定价公式为:

其中C表示欧式看涨期权的价格,r表示无风险利率,X表示期权的执行价格,S(T,i)表示标的资产在到期日T的第i条路径模拟价格。
2 数据分析与实证
2.1 数据的选取与准备
本文实证的数据来自WIND金融数据库,研究的期权为长电CWB1(580007),其标的股票为长江电力(600900),选取长江电力上市之日2003年11月18日至2007年3月19日的日收盘价为样本来进行GARCH模型的估计,共806个数据,其收益率按照如下的公式来计算:

其中Rt表示股票的日收益率,St为股票的每日收盘价。
2.2 实证分析
2.2.1 描述性统计(见图1,图2)
图2的结果见表1。
由图1可以看出长江电力日收益率的波动都表现出时变性、突发性和集群性。由图2的结果可看出其收益率分布都是略微右偏的,其峰度明显要高于正态分布的峰值3,所以具有一般金融时间序列“尖峰厚尾”性质。通过雅克贝拉检验可以得出长江电力日收益率序列的分布是显著的异于正态分布的,初步具备建立GARCH(1,1)模型的条件。
2.2.2 平稳性检验
从上面的统计分析能够知道,收益率序列围绕着均值上下波动,不存在趋势,因此,对沪深两市的收益率序列做带截距项不带时间趋势滞后4阶的ADF检验,可以得到表2。

表1 长江电力日收益率序列的统计特征
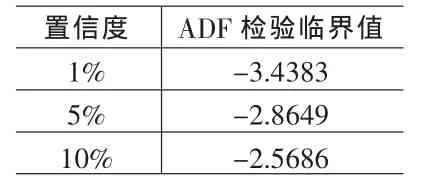
表2 长江电力日收益率序列的增广迪基富勒检验

表3 GARCH(1,1)方差方程的建模结果

表4 ARCH-LM检验结果
由长江电力日收益率序列的增广迪基富勒检验得出,ADF检验统计量为-12.952,P值接近为0,说明长江电力的收益率序列均在1%的显著性水平下拒绝存在单位根的原假设,由此得到长江电力的收益率序列是平稳的,无需差分则可以直接建立模型。
2.2.3 建立GARCH(1,1)模型
对长江电力建立GARCH(1,1)模型,可得表3。
即:
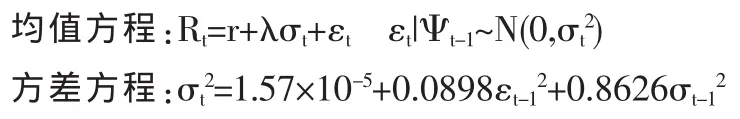
由表3可以看出,方差方程中所有系数都是统计显著的,且所有系数均大于 0,α1+β1=0.9524<1,满足 GARCH(1,1)模型中参数的约束条件,由于ARCH项系数和GARCH项系数之和为0.9524,又非常接近于1,说明外部冲击引起长江电力的波动影响时间会比较长,持久性特征明显。
2.2.4 GARCH(1,1)模型的ARCH-LM检验
对GARCH(1,1)模型的残差进行滞后4阶的ARCH-LM检验,其结果见表4。
相伴概率为0.8827,接受原假设,认为残差序列不具有ARCH效应,说明上面的GARCH(1,1)模型很好地消除了残差序列的条件异方差性。
2.3 期权定价蒙特卡罗模拟方法的R语言实现
R语言的实现程序见附录。附录中的程序构造了一个函数,只要输入离行权日的天数n、股票的前一天收盘价格s0作为初始价格、权证的行权价格X和股票的历史波动率sigma0还有单位风险费用 (这里假设为0.25),并且选取2006年一年整存整取的利率2.52%作为无风险利率,就可以通过10000次的模拟股价路径,算出10000个在行权日当天的股票最终价格,从而得出以其为标的资产的权证的价值。则最终运算得到的模拟价格与真实价格的比较见表5。
利用偏离度来界定蒙特卡罗模拟方法的优劣,从定量的方式着手,验证基于GARCH模型的蒙特卡罗定价方法的有效性。

平均偏度计算方法:

其中Pr为真实价格,Ps为蒙特卡罗模拟价格。则由此可以算出,蒙特卡罗模拟价格与真实价格之间的平均偏离度为 4.843%,说明 GARCH(1,1)模型对权证的定价偏差不大,结合了GARCH模型的蒙特卡罗方法十分有效。
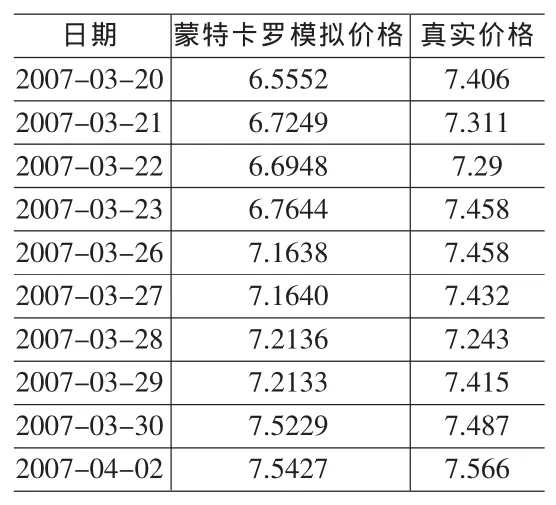
表5 蒙特卡罗模拟价格与真实价格对比
3 结论
本文利用多种金融时间序列分析方法与统计手段,对标的股票长江电力(600900)和权证长电 CWB1(580007)进行实证分析,结合GARCH模型和蒙特卡罗模拟方法对长电CWB1进行数值定价,得到如下结果:
(1)长江电力的股票日收益率基本满足一般金融时间序列具有的“尖峰厚尾”特征,而拟合出来的GARCH(1,1)模型能很好地模拟其波动率,各项系数都十分显著,ARCH项系数和GARCH项系数之和为0.9524,非常接近于1,说明外部冲击引起长江电力的波动影响时间会比较长,持久性特征明显。
(2)虽然运用了期权的定价方法,可是长电CWB1不是真正的期权产品,理论上和期权还是有一些出入的,权证是由公司发行的,发行数量上是有限的,容易被人操纵价格,影响定价的准确性。
(3)卖空机制能使股票市场的价格更加接近于真实价格,对实现股票市场的有效性有着重要的意义。由于当时我国股票市场不允许卖空,使得套利无法进行,市场的投机成份较多,价格的上下波动大,也会增加定价的难度。
(4)在中国权证市场上多数都是百慕大式的权证,是介于欧式和美式的一种权证,蒙特卡罗方法由于其独特的性质,一般用来模拟欧式的权证,不过总体来说,基于GARCH模型的蒙特卡罗模拟值和真实值之间的平均偏离度只有4.843%,定价的准确性还是相当高的。
[1]Duan J.The Garch Option Pricing Model[J].Mathematical Finance,1995,5(1).
[2]Duan J,Simonato J.American Option Pricing under GARCH by a Markov Chain Approximation[J].Journal of Economic Dynamics and Control,2001,25(11).
[3]Duan J,Zhang H.Pricing Hang Seng Index Options around the Asian Financial Crisis-A GARCH Approach[J].Journal of Banking&Finance,2001,25(11).
[4]汪来喜,丁日佳.基于GARCH模型的股票期权定价方法研究[J].金融理论与实践,2008,(2).
[5]王健,李超杰,何建敏.有交易成本的GARCH-扩散期权定价模型[J].东南大学学报(自然科学版),2006,(1).
[6]张敏,王键.Monte-Carlo模拟法在期权定价中的应用[J].湖南商学院学报,2003,(4).
[7]R Tsay.金融时间序列分析[M].北京:机械工业出版社,2006.
(责任编辑/浩 天)
F830.91
A
1002-6487(2010)23-0163-03
