深埋非圆形地下洞室围岩应力解析分析的“当量半径”法＊

刘长武,曹 磊,刘树新

(1.水利学与山区河流开发保护国家重点实验室,四川成都 610065; 2.四川大学水利水电学院,四川成都 610065)

深埋非圆形地下洞室围岩应力解析分析的“当量半径”法＊

刘长武1,2,曹 磊1,2,刘树新1,2

(1.水利学与山区河流开发保护国家重点实验室,四川成都 610065; 2.四川大学水利水电学院,四川成都 610065)

受施工方法与施工手段的限制,常见的地下洞室断面形状都是矩形、直墙半圆拱形等典型的非圆形断面形式。限于目前弹塑性力学和岩石力学的发展水平,除椭圆等极少数非圆形地下洞室周边的应力分布有理论解析解外,其它非圆形地下洞室周围的应力分布都缺乏精确的理论解析解,直接影响了地下洞室的围岩稳定性分析和支护形式与支护参数设计。本文在全面分析影响地下洞室围岩稳定性主要因素的基础上,系统论述了地下洞室深埋的3重含义;分析了采用外接圆半径法进行非圆形地下洞室周围应力分布理论分析时存在的主要问题;提出了以“当量半径”为特征尺寸的等面积虚拟圆来替代实际非圆形地下洞室的简化方法和“当量半径”的计算公式,为非圆形地下洞室的围岩稳定性分析和支护形式与支护参数设计提供了科学的理论依据。

深埋;非圆形;地下洞室;应力分布;当量半径

1 引言

为了实现地下有用矿物开发、开采和地下空间开发、利用的目的,人们必须在地层(岩层或土层)中开凿大量的、各种形状和尺寸的地下巷道、地下隧道、地下隧洞和地下洞室(为叙述方便起见,以下统称为地下洞室),地下洞室的开挖与维护成为地下工程领域最重要的研究内容之一。

地下洞室的开掘工作破了地层原岩应力的平衡状态,导致岩、土体内部的应力重新分布。当重新分布后的应力超过岩、土体的极限强度时,地下洞室周围的岩、土体发生破坏,这种破坏将持续到岩、土体内部再次形成新的应力平衡为止[1]。此时,在地下洞室周围的岩、土体内形成一个与原岩应力场完全不同的新的二次应力场,引发不同程度的应力集中,并在洞室周边围岩内形成一定范围的极限平衡区[2]。

显然,这种地下洞室开挖诱发的地层空间应力场的演变变化是引起洞室围岩变形、移动垮落和支架受压损坏等矿压显现的根本作用力,是决定顶板灾害事故发生与否的主要因素之一。该问题的深入研究是地下工程界一个永恒的重要主题。

2 影响地下洞室周边应力分布的主要因素

与一般的地面构筑物不同,地下洞室是在天然状态下的岩、土体内开挖的,岩、土体自身的物理、力学性质对支护结构的荷载及其稳定都有重要的影响。同时,围岩不仅会对支护结构产生荷载,而它本身又是一种承载体,地下洞室支护结构与围岩之间存在着一种特殊的围岩——支架相互作用关系。充分调动围岩自身的承载能力,协调围岩——支架相互作用关系,可以实现地下洞室支护的优化设计。

全面分析围岩——支架的这种相互作用关系可以看出,虽然影响地下洞室周围应力分布及其支护结构稳定性的因素很多,但归纳起来,这些因素可以概括为岩、土体容重、抗压强度、粘结力和内摩擦角等自身的物理、力学参数;与地下洞室埋深及区域构造应力有关的原岩应力和地下洞室的数量、形状与尺寸等人为扰动因素等3大类。在这3类影响因素中,岩、土体的物理力学性质是决定地下洞室开挖后围岩稳定与否的内因;由自重应力和构造应力等构成的原岩应力及其扰动后的重新分布,是引起地下洞室围岩变形、破坏的动力外因;而地下洞室的数量、形状和尺寸集中反映了地下有用矿物开采和地下空间开发利用过程中的人们对天然岩、土体的人为扰动程度。

岩、土体自身的物理力学性质对地下洞室围岩稳定性的影响,人们已进行了多年的研究和探索,因此这里重点讨论地下洞室的埋藏深度和地下洞室的形状和尺寸等人为扰动因素与地下洞室周围应力分布的关系。

3 地下洞室深埋的三重含义

地下洞室的埋藏深度不仅决定了原岩应力场中自重应力的大小,而且还直接影响地下洞室支护结构上的荷载及其分布形式。因此,地下洞室的埋藏深度是影响洞室围岩稳定性分析和支护结构形式选择与支护参数设计的主要因素之一。

到目前为止,关于“浅埋”和“深埋”的划分,国内外还没一个能被广大岩土工作者所普遍接受的界定。不同工程领域关于深与浅的含义也不尽相同,并且随着时间的变化与技术的发展、以及地下工程向地层更深处的发展,浅埋与深埋的工程界定标准及其所关注的问题也有所不同。

目前国内地学界对深埋和浅埋的划分,大多是以铁路隧道工程界的划分标准为基本界定范围,再适当考虑自身领域所具有的特性而界定的。

根据埋深的大小,我国早期将隧道划分为深埋隧道和浅埋隧道两种[3],现行的铁路隧道设计规范[4]和公路隧道设计规范在计算围岩压力时,也都采用该划分方案。该方案划分深埋的临界深度是以隧道上方覆盖岩、土层的厚度能否形成自然平衡拱(压力拱)为原则而确定的。因此,围岩的性质与类别不同,所划分的界定深度也不完全相同。深埋界限一般采用塌方平均高度的2～2.5倍而划定,如表1所示[3]。

根据表1可以看出:对于山岭隧道,埋深超过50m时,上方覆盖层岩、土体基本上都能形成自然平衡拱,亦即属于深埋隧道的范畴。

表1 各类围岩塌方高度平均值和深埋界限值

暗挖城市地铁区间隧道、部分油气地下储库和部分埋深较浅的铁路、公路隧道等大都属于上述意义上的浅埋地下洞室。而大型地下越岭隧道、各种地下采矿巷道、地下核废料处理洞室等往往大都属于深埋地下洞室。

区分深埋与浅埋的基本目的,是针对不同的地下洞室类型,进行相应的围岩压力及支护结构荷载估算。然而,随着地下工程向地层更深处的发展,埋藏深度的大小对地下工程的影响已远远超出一般意义上的静力学范畴,在工程施工及其后的维护过程中出现的动力学现象——岩爆与冲击地压、高压突水、高压有害气体与岩(煤)突出;以及高地温、和软岩变形等问题已成为影响工程设计与施工的主要因素。虽然上述某些现象在个别浅埋工程中也有所发生,但大部分现象还是出现在埋藏深度大于几百米的深埋地下工程中,而且随着埋藏深度的增大,事件发生的几率也有随之增高的趋势。

因此,再将埋深几十米的地下洞室和埋深上千米的地下洞室简单地用深埋工程归结为一类显然是欠合理的,从而许多隧道工作者又赋予“深埋”以新的含义,也有学者把深埋的临界值确定为500m。徐则民等则在尊重即有划分方案的基础上,将隧道按埋深划分为浅埋、深埋和超深埋三种形式,如表2所示[3]。

表2 硬岩隧道埋深划分方案

埋藏深度对地下洞室围岩稳定性的影响除上述两重含义外,还与洞室周围应力分布的分析计算有直接关系。只有当洞室的高度h远小于洞室的埋藏深度H时,沿洞室高度的应力变化才能忽略不计,如图1所示。根据若干资料的分析结果[5]:在岩体的自重应力场中,当洞室的埋藏深度H大于洞室高度h的3倍时,可以近似假定洞室围岩的受力状态如图2所示,亦即上、下的垂直应力都是匀等的,其值为Pν=γ·H;围岩两侧的水平应力Ph也假定为均匀分布,其值为Ph=λ·γ·H=λ·Pν。

在地下洞室为“深埋”圆形洞室的前提下,采取上述的简化假定后,可以借助弹性力学中计算有孔平板在周围外荷载作下的应力公式来分析地下洞室周围的应力分布规律。

4 非圆形地下洞室的外接圆半径

根据弹塑性理论和岩石力学的基本原理,两直线相交处剧烈的应力集中现象,使得地下洞室的形状对其周围应力分布的影响,特别是折边形地下洞室棱角对其附近应力分布的影响是十分显著的。

限于目前弹塑性力学及岩石力学的发展水平,除圆形、椭圆形等少数洞室断面形状周围的应力分布有理论解析解外,直墙半圆拱形、矩形等许多地下工程中常用的洞室断面形状周围的应力分布都缺乏精确的理论解析解。这些形状地下洞室所引起的应力重新分布情况,多通过光弹性试验及计算机数值模拟等方法来研究确定。

虽然通过计算机数值模拟等方法可以获得非圆形地下洞室周边的应力分布情况,但在工程中要想应用这些计算结果却往往是比较困难的。而且重点凸显这些形状特点的形状效应多局限在棱角等局部地方,对总体的地层空间应力场的演变变化规律影响不大。所以,对于非圆形地下洞室,采用非圆形地下洞室的圆形标准化法来考虑地下洞室的断面尺寸和形状的影响,是解决该问题的一条有效途径。

作非圆形地下洞室的外接圆,用该外接圆的半径代表实际地下洞室的特征尺寸,外接圆半径可以用解析计算法或几何作图法求得[6],如图3所示。

用这样的方法求解出的特征尺寸(外接圆半径)已包含了形状因素,不需再用系数来修正。

把各种典型的非圆形地下洞室转(简)化为以此外接圆半径为特征尺寸的圆形地下洞室后,就可以利用圆形地下洞周围应力分布的各种理论和公式对洞室周围的应力分布及洞室周边位移等进行理论解析。

图3 常见的典型非圆形地下洞室的外接圆几何作图法

这种以外接圆半径表示非圆形地下洞室特征尺寸的简化方法,基本原理简单、易于掌握。但是,用这种方法所获得的分析结果显然相对保守;同时,对于单边斜梯形等特殊形状的地下洞室,用解析法求解外接圆半径的计算公式相对复杂;而用几何做图法求解时,不同的作图者之间往往存在着一定的相对误差。因此,工程应用上仍然受到很大的限制。

5 非圆形地下洞室的“当量半径”及其工程应用

针对非圆形地下洞室解析分析的外接圆半径法存在的一系列问题,从易于现场应用的角度出发,这里提出了以一个与非圆形地下洞室断面积相等的虚拟圆半径为特征尺寸的非圆形地下洞室解析分析的“当量半径”法。基本原理就是用一个与非圆形地下洞室断面积相等的虚拟圆来简化非圆形地下洞室,该虚拟圆的半径代表实际非圆形地下洞室的“当量半径”,通过对该虚拟圆周边应力分布的理论分析来获得非圆形地下洞室周围应力分布的解析解。

5.1 非圆形地下洞室的“当量半径”

假设有一个与非圆形地下洞室断面积相等的虚拟圆,则该虚拟圆的半径r0为:

式中:r0为虚拟圆的半径,m;S为实际非圆形地下洞室的断面积,m2。

地下洞室形状对洞室周边附近的应力分布是有很大影响的。因此,必须对公式(1)计算出的虚拟圆半径进行修正,以便充分反映地下洞室的形状效应,如式(2)所示[7]。

式中:r为非圆形地下洞室的“当量半径”,m;k为洞室断面形状修正系数;其它符号意义同前。

根据实测与计算结果得出不同形状地下洞室的断面修正系数值如表3所示[7]。

表3 地下洞室断面形状修正系数

5.2 工程应用

上海大屯能源股份有限公司徐庄矿7172工作面位于微山湖沼泽区下,地面标高+31.97m,地下该面西部为东七上山,南部为未开拓区,深部为7174工作面,运输巷最深部标高为-295m。工作面开采7#煤。煤层平均厚5.65m,容重13.7kN/m3;直接顶为砂质泥岩,平均厚度2.40m;老顶为细砂岩和中砂岩,平均厚度9m,上覆岩层的加权平均容重为25 kN/m3;煤岩体力学参数修正系数的统计结果为1/3(即:煤岩体强度为煤岩块强度的1/3)。

采用厚煤层放顶煤一次采全高回采工艺,运输巷为沿煤层底板掘进、留部分顶煤的全煤巷道。巷道断面为4.2×2.6m的矩形。

实验室测得煤的粘结力c=5.13MPa;内摩擦角φ=29.7°;剪切模量G=0.793×103MPa,计划采用锚喷网支护方式,因此需要对锚杆长度等支护参数进行设计。

根据上面给定的条件,运输巷的最大埋藏深度为327 m(295+31.97),按海姆假说估算原岩应力为:

巷道断面的实际形状为4.2×2.6m的矩形(非圆形),按式(2)可以求得该巷道的“当量半径”r为:

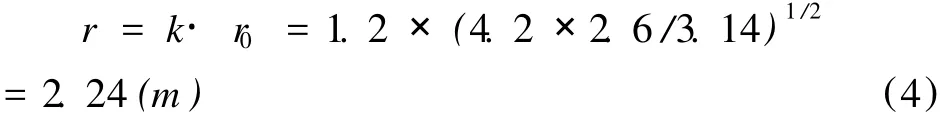
以计算获得的当量半径为特征尺寸,按弹性力学理论,可以计算出不受回采工作面采动影响时,静水应力状态下巷道周围极限平衡区半径R为:

式中:K2为煤岩体力学参数修正系数,等于1/3; Pi为支护系统对巷帮围岩提供的支护强度,约等于0。

煤体中极限平衡区的宽度△为:

从而可以确定锚杆的长度L为:

式中:L1、L2分别为锚固段长度和锚杆外露长度,m。

考虑实际锚杆的加工,实际锚杆长度取整数2 m。确定了锚杆长度后,可以进一步对锚杆直径和锚杆的间、排距等其它参数进行计算和分析,限于篇幅这里不再述及。

6 结语

以修正的等面积虚拟圆半径为特征尺寸,对地下工程施工、建设过程中经常遇到的矩形、直墙半圆拱形等非圆形地下洞室进行简化,借助弹塑性理论中计算有孔平板在周围外荷载作下的应力公式,可以获得非圆形地下洞室周围近似的应力分布规律,进而可以得到洞室周边围岩内的极限平衡宽度等与洞室围岩稳定性直接相关的重要参数。从而为地下洞室的支护形式选择与支护参数设计提供了科学的理论依据。

REFERENCES

[1] 陈炎光,陆士良.中国煤矿巷道围岩控制[M].徐州:中国矿业大学出版社,1994.

[2] 钱鸣高,刘听成.矿山压力及其控制[M].北京:煤炭工业出版社,1984.

[3] 徐则民,等.深埋特长隧道及其施工地质灾害不[M].成都:西南交通大学出版社,2000.

[4] 铁道部第二勘测设计院主编.铁路隧道设计规范[M].北京:中国铁道出版社,1998.

[5] 徐志英.岩石力学[M].北京:中国水利水电出版社,2002.

[6] 华安增.矿山岩石力学基础[M].北京:煤炭工业出版社, 2002.

[7] 刘长武,等.地层空间应力场的开采扰动与模拟[M].郑州:黄河水利出版社,2005.

M ethod of"Equivalent Radius"for the Analyzing Rock Stress of High-buried Non-circular Underground Chambers

L IU Chang-wu1,2,CAO Lei1,2,L IU Shu-xing1,2
(1.State KeyLaboratory of Hydraulics andMountain River Engineering,Chengdu 610065,Sichuan,China; 2.College ofWater Resource and Hydropower,Chengdu 610065,Sichuan,China)

Be hedged in with constructionmethods andmeans,themost common sectional shapesof underground chambers are all rectangle and semicircularwhich belong to typical non-circular cross section for ms.Due to the development of current plasto-elasticity and rockmechanics,stress distribution around non-circular underground chambers has no accurate analytical solution except a few non-circular underground caverns,which directly influences stability analysison the surrounding rocksof underground chamber and design of supportpatterns and parameters.On the basis of analyzing the main factorswhich influence stability of surrounding rocks of underground chamber,the paper discusses systematically three definitions of the high-buried underground chamber;analyses themain problems in theoretical analysis about stress distribution in surrounding rock of the non-circular underground chamberwhen the circumradiusmethod is adopted in;and puts forth a calculation for mula of"equivalent radius"and a s implified method for equal area virtual circle whose characteristic d imension is"equivalent radius"takes the place of practical non-circular underground chamber,which provides the scientific theory reference for stability analysis of surrounding rock mass of underground chamber and design of support patterns and parameters.

high-buried;non-circular;underground chamber;stress distribution;equivalent radius

TD322+.4

:A

:1009-3842(2010)01-0001-05

2010-01-04

＊

国家自然科学基金资助项目(项目批准号:50879049;50574064);国家重点基础研究发展计划(973计划)(项目编号: 2010CB226802)

刘长武(1963-),男,汉族,黑龙江大庆人,工学博士,博士后,四川大学水利水电学院教授,博士研究生指导教师,主要从事矿业工程和地下工程方面的科研与教学工作。