《概率论与数理统计》教学改革研究与探索

时 凌,魏代俊,吴 勇(湖北民族学院 理学院,湖北 恩施 445000)

《概率论与数理统计》教学改革研究与探索

时 凌,魏代俊,吴 勇
(湖北民族学院 理学院,湖北 恩施 445000)

针对理工科学生概率论与数理统计课程的教学改革进行了研究与探索。从重点教堂内容、课程体系、培养创新能力和应用能力的教学模式以及课时分配等进行了一系列探讨。

概率论与数理统计;随机现象;教学改革

概率论与数理统计是专门研究和探索客观世界中随机现象统计规律的一门数学学科,随着现代技术的飞跃发展,不论是在自然科学领域还是在社会科学领域中,传统的肯定性数学已经不能合乎要求地解决所遇到的各类理论问题及应用问题,因而在这个过程中,随机性数学-概率论与数理统计得到了蓬勃发展。它不仅形成了结构宏大的理论体系,而且在许多领域中都得到了广泛的应用,如金融、保险、经济与企业管理、工农业生产、军事、工程技术等,同时在许多新兴学科与边缘学科,如信息论、排队论、对策论、人工智能等领域中也有广泛的应用。反过来,这些领域中的许多新课题又促进了概率论与数理统计的进一步发展,从而使得概率论与数理统计成为了近代数学中最活跃的分支之一[1,2]。

鉴于概率论与数理统计的这些深刻的实际背景,这门处理随机现象的数量关系与数量规律性的课程越来越受到人们的重视,成为了大学数学里的一门十分重要的基础课程。目前,研究生入学数学统考试题中,概率论与数理统计所占比例达到20%-25%。因此学好和掌握好概率论与数理统计不仅是将来从事科学研究和实际工作的需要,更是高度发展的现代化社会对现代化人才提出的基本要

求[3,4]。

然而就我国目前的现状而言,多数高等院校关于概率论与数理统计的教学都没有跟上时代的要求和需要,本科教学仍停留在理论分析、问题的抽象与求解。我们知道,概率论与数理统计不同于高等数学、线性代数等其他研究确定性的数学分支,由于学生在学习概率之前,在数学的先期课程中打下了非此即彼、非对即错的两极思想模式,现在转入研究随机现象,需要用一种全新的思维方式思考问题,这使得学生们感到很不习惯,抽象不易理解,从而无法在本质上把握理论和概念。因此研究《概率论与数理统计》课程的教学体系就被赋予了重要的意义[5]。

一、课时分配

理工科专业《概率论与数理统计》的课时分为48、56和64几种,以概率论为主,而数理统计相对较少,48学时的只有4周时间,56学时的只有5周时间、64学时的有6周时间,主要内容为:样本及抽样分布,参数估计和假设检验。课时分配为:1.5,1.5,1、1.5,1.5,2或者2,2,2。

二、教学方法

“满堂灌”、“黑板+粉笔”“教师讲,学生听”这种传统的教学方法,不利于培养学生的思维能力和创新意识,从而导致学生缺乏思维方法的训练,思维能力不强,创新意识较差。为了改变这种状况,需要改变教学中的以教师为中心的教学结构,建立一种既能发挥教师的指导作用,又能充分发挥学生学习主动性和积极性的新型教学模型。由于概率论与数理统计课在教学中所占的课时较少,但涉及的内容较多,非常适合进行教师与学生的互动式教学.同时可以充分利用现代的教学手段,使教学过程更加生动、活泼。充分利用现代的教学手段,利用课件和讲授相结合的教学模式进行教学。例如在讲授χ2-分布、t-分布和F-分布时,可以充分利用课件,介绍分析密度函数在不同参数情况下的变化趋势,从而加深学生对χ2-分布、t-分布和F-分布变化趋势的认识,为讲授假设检验打好基础。

三、重点教学内容

如何在课时少内容多的情况下,既能满足考研学生对数理统计内容的基本要求,同时又能满足一般学生掌握数理统计的需求呢?我们从以下几个方面入手,着力数理统计重点教堂内容的改革,收到了较好的效果。

1.讲清一个基本框图

数理统计中几个基本而重要的概念:总体、样本和样本值之间的关系如图1所示.图1是数理统计中非常重要的图形,贯穿于整个数理统计的教学之中,反映了数理统计的基本思想。由于总体数量相当庞大或者对个体进行试验具有破坏性(如水炮弹能否引发爆炸)或者费时耗资大等原因,对总体的研究转为对总体中的部分个体的研究,即从总体中抽取部分个体进行研究。为了充分体现总体的性质,对这部分个体要求具有独立性和代表性,从而形成简单随机样本。为了数学角度来研究总体,进而引入了样本值。由样本值的性质推断出总体的性质。对于总体可以从两个方面来理解[6,7]:

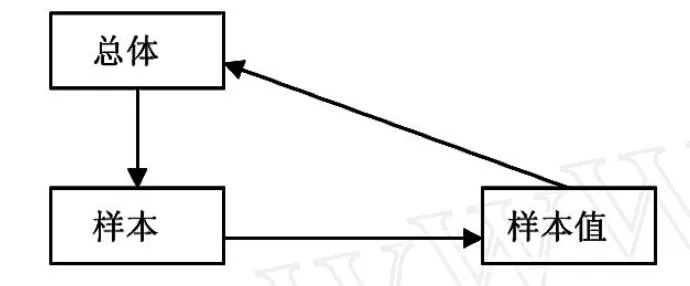
图1 基本框图

2.四大分布

数理统计中的四大分布为:正态分布、χ2-分布、t-分布和F-分布,其中正态分布是最重要的分布,其基本内容可以归纳如下:

(1)标准化

由于χ2-分布、t-分布和F-分布的密度函数一般都比较复杂,因此必须讲清这几个分布的构成,分布函数的变化趋势及其特殊性质。

(3)一个基本定理

抽样定理中一个必须掌握的基本定理是Fisher引理, Fisher引理是抽样定理中最基本的一个定理,不仅应用于单正态总体的情况,而且也可以应用到两个正态总体的情况.同时也是抽样定理中其他定理的基础,其叙述如下:

假设ξ1,ξ2,……ξn是来自正态总体N(μ,σ2)的样本, ?ξ是样本均值,?S是样本方差,则有:

(4)参数估计有两种方法

参数估计中常用的方法有矩估计法和极大似然法。

(ⅰ)矩估计是基于一种简单的“替换”思想建立起来的一种估计方法,即用样本矩代替总体矩的一种估计方法。该方法从计算角度来说方法简单,容易掌握;从理论上来看第一样本矩p-收敛到总体矩;第二矩估计是无偏估计;第三矩估计是相合估计。所以一般情况下应先求统计量的矩估计,如果求不出来再考虑应用极大似然估计。但矩估计的缺点是没有充分利用分布提供的信息。一般场合下,矩估计不唯一。

(ⅱ)极大似然估计的关键是似然函数的构造。似然函数的实质是样本的联合分布律或者联合密度函数,在讲授的过程中必须讲清楚这点;其次是只对未知参数求导数或者偏导数;最后需用实例说明当极大似然法行不能时可用极大似然原则来求是极大似然估计。

(5)估计的评价

估计量的评价有三个标准:无偏估计、最小方差无偏估计和相合估计。无偏估计的实质是无系统偏差,但无偏估计有时不唯一,因此评价标准中引入了最小方差无偏估计。在大样本的情况下又引入了相合估计。相合估计是对估计量的一个基本要求,不具备相合性的估计量是不予以考虑的。

(6)带概率意义的反证法

假设检验的逻辑推理与高等数学是完全不一样的,它的基本原理是小概率事件原理:小概率事件在一次试验中几乎不发生.但需要说明的是:几乎不发生不等于一定不发生。

一般的反证法要求在原假设成立的条件下导出的结论是绝对成立的,如果事实与之矛盾,则完全绝对地否定原假设.但概率反证法的逻辑是:如果小概率事件在一次试验中居然发生,我们就有很大的把握否定原假设.这样的不同应该在教学中重点强调,使学生明白如何理解和如何应用.

(7)两类错误

假设检验是根据样本的信息并依据小概率原理作出接受还是拒绝原假设的判断。由于样本具有随机性,因而假设检验所作出的结论有可能是错误的,这种错误有两类,如表1所示:

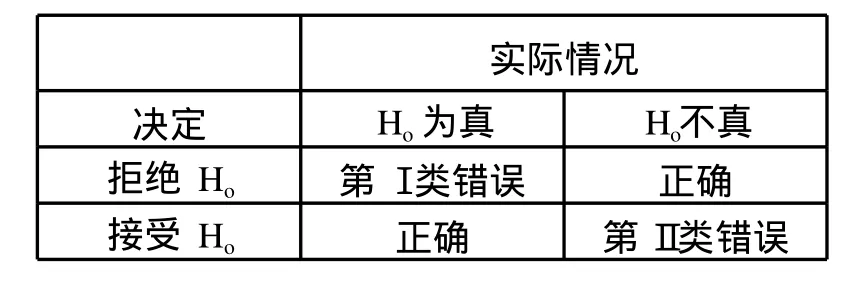
表1 假设检验的两类错误

犯第Ⅰ类错误的概率是显著性水平α,α=P,{拒绝Ho|Ho为真},犯第Ⅱ类错误的概率记为β,β=P{接爱Ho|Ho不真}。

两类错误之间的关系是此消彼长:当α增大时β减小,当β增大时α减小。我们要想同时减少犯两类错误的概率,只有通过增加样本容量。但样本容量的增加又会受许多因素的限制,所以人们想办法对两类错误加以控制,由于犯第Ⅰ类错误的概率是可以由研究者控制的,因此在假设检验中,人们往往先控制第Ⅰ类错误的发生概率。当样本容量n一定时,若减少犯第Ⅰ类错误的概率,则犯第Ⅱ类错误的概率往往增大。

当然假设检验的计算问题可以通过实例进行讲解,也应该引起重视。总之,只要我们讲清楚并使学生真正掌握了上述几个问题,数理统计的基本方法、基本理论和基本概念也就掌握了。

[1]王翠香.“概率论与数理统计”教学的几点体会[J].高等理科教育,2006,69(6):35～37.

[2]张景祥,唐旭清.概率统计课程的改革与实践[J].江南大学学报(教育科学版),2007,27(2):89～93.

[3]刘琼荪,钟波.将数学建模思想融入工科”概率统计”教学中[J].大学数学,2006,22(2):152～155.

[4]丁淼,边振华,于颖.概率论教学方法改革[J].科技信息,2007,34(4):553～554.

[5]陈建兰,吴明,孙伟良.概率论与数理统计教学改革[J].杭州电子科技大学学报(社会科学版),2005,2 (1):58～60.

[6]盛骤,谢式千,潘承毅,等.概率论与数理统计(第4版) [M].北京:高等教育出版社,2009.

[7]梁之舜,邓集贤,杨维权,等.概率论与数理统计(第3版)[M].北京:高等教育出版,2005.

G420

A

1006-5342(2010)10-0145-03