点光源劈尖干涉的条纹分布特征

王开圣,赵志敏,杨雁南

(南京航空航天大学理学院,江苏南京211100)

点光源劈尖干涉的条纹分布特征

王开圣,赵志敏,杨雁南

(南京航空航天大学理学院,江苏南京211100)

在有限远的点光源照射下,导出了劈尖干涉的明、暗纹条件,通过Matlab软件,用数值分析方法给出了劈尖表面条纹分布特征,讨论了光源距离对表面条纹分布的影响.

劈尖干涉;点光源;数值分析

1 引 言

在讨论厚度不均匀的薄膜干涉时,大学物理教科书往往将光源看成无限远,近似用平行光处理,但实验室常用扩展光源代替平行光源(如劈尖以及牛顿环实验).扩展光源可看作是由大量的独立点光源所组成,每个点光源都可能在空间产生其各自的干涉图样,相互叠加后,总的干涉条纹的明暗对比度下降,使得干涉条纹只能在空间某些区域出现,由此引出了干涉的定域问题,文献[1-3]对扩展光源劈尖干涉的定域中心和定域深度等问题做了详细的研究,指出了在光源尺度很小、光源距离很远、劈尖角很小的条件下,条纹定域在劈尖表面及其附近.然而,实际做实验时并不把扩展光源放在所谓的很远处,一般离开数十厘米左右,用显微镜或眼睛就可观察到劈尖表面的干涉条纹,而且处理数据仍沿用平行光照射的公式,对此物理教科书及实验指导书都缺少详细解释.关于这个问题,笔者认为除了与定域干涉有关以外,还与点光源自身干涉条纹的分布有关,因为条纹间距、分布均匀性等是以点光源干涉为基础.本文以劈尖干涉为研究对象,通过Matlab软件,用数值计算方法描述点光源劈尖干涉条纹的分布特征,定量分析点光源距离对干涉条纹的影响.

2 劈尖表面的明、暗纹条件

模拟计算依据的点光源劈尖干涉光路如图1所示,折射率为n的介质劈置于空气中,劈尖顶角为θ,为简化光程差的表达式,便于讨论,点光源S置于劈尖顶端O的垂线上,与劈尖表面距离为R.从光源S发出的光SA在劈尖上表面折射进入劈尖,在劈尖下表面B处反射回上表面C处,再经过折射返回空气中,与从光源S发出的另一光线S C在C处相遇产生干涉,2束光的光程差决定了C点的光强.

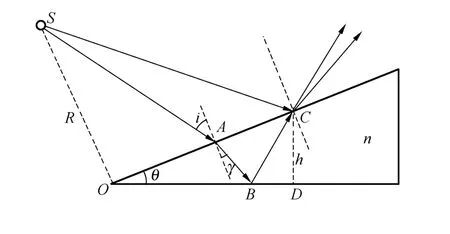
图1 点光源劈尖干涉光路图

设光SA的入射角为i,光AB的折射角为γ,劈尖C处的厚度CD 为h.

当光源无限远时,SA与S C可看成平行光,且劈尖顶角θ非常小时,光程差的计算可按文献[4]上的公式来计算,

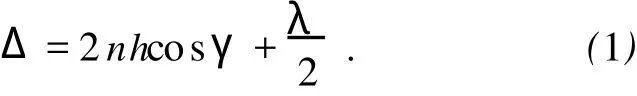
若光源无限远,但考虑劈尖顶角θ对光程差的影响时,光程差的计算可按下式计算[5]

明暗纹条件由下式给出,从而可以确定明、暗纹的位置:

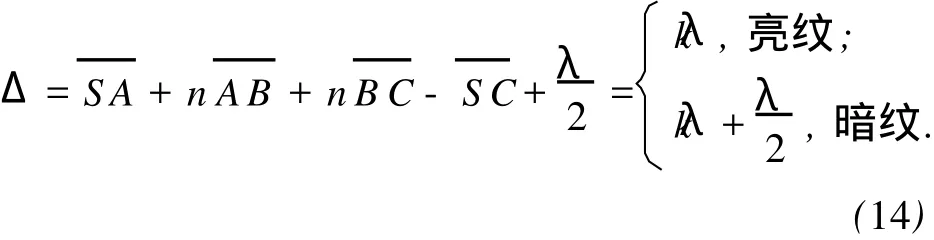
3 条纹分布特征的数值分析

干涉条纹的分布特征包含在明、暗纹表达式(14)中,由于光程差公式较复杂,难以从解析结果直接分析和归纳,所以下面利用Matlab数值计算及图示化功能,分析干涉图像特征,研究光源距离对干涉图像分布的影响.

在数值计算时,取介质劈折射率n为1.2,顶角θ为0.01°,采用钠黄光光源,主要由589.0 nm和589.6 nm谱线构成,故谱线宽度Δ λ= 0.6 nm,则其相干长度为

求解步骤如下:

1)赋予光源距离R一初值;

2)取入射角i初值为0,步长为1°×10-7,末值为85°;

3)计算折射角γ及对应的劈尖厚度h;

4)计算光程差Δ,并判断是否小于相干长度0.58 mm,若否,中止运算,若是,进行下一步骤;

5)计算光程差Δ与波长λ的比值Δ/λ,即条纹级数k,判断比值是否为整数,精确到10-4,若不为整数,返回2)选择下一个i值,重复2)～5);

6)若Δ/λ比值是整数,保存i、条纹级数k及相应的条纹位置OC(k),返回2)选择下一个i值,重复2)～6)直至最后一个i;

7)计算相邻的两条纹间的距离OC(k+1)-OC(k);

8)赋予光源距离R另一个值,重复2)～7);

9)结果图示化.

计算结果如图2所示,给出了50,80,110, 200,500,800 mm不同光源距离时,条纹间距随级数的变化情况,图中k为条纹级数,如k=1时,条纹间距对应第1级暗纹与0级暗纹的间距,k= 2时,条纹间距对应第2级与第1级的暗纹间距,依次类推.

从图中可看出:

a.条纹不是等间距分布,相邻条纹间距随级数k增大而增大,即离劈尖顶点愈远,间距愈大.

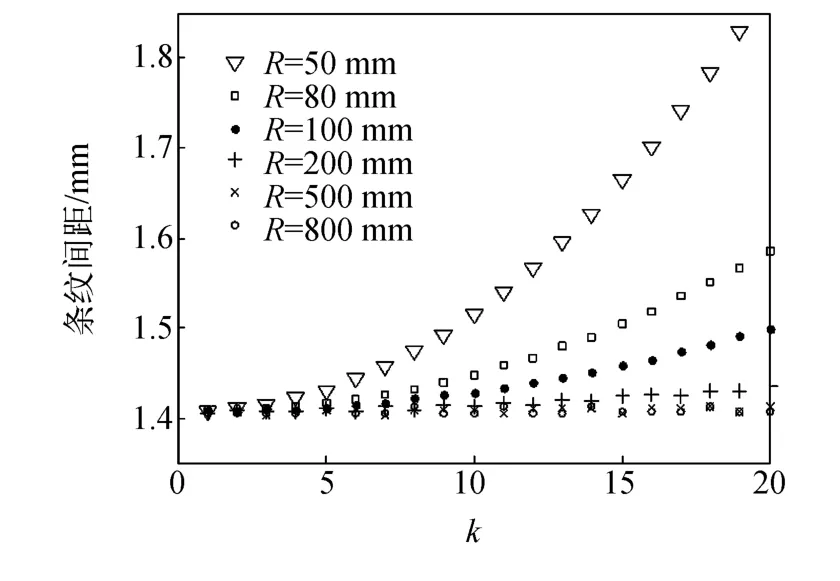
图2 不同光源距离时条纹间距随级数k的变化

b.随光源距离的增大,条纹间距变小,条纹变密,其中高级数的条纹间距比低级数的减小幅度大.

c.这种条纹间距不均匀性在光源距离较小时比较明显,但随光源距离的增大,条纹间距逐渐均匀.对文中模拟所用的劈尖,当光源距离小于100 mm时,条纹间距随级数变化很快,光源距离达到200 mm时,条纹间距随级数变化趋缓,在光源距离超过500 mm后,条纹间距随级数变化很小,可看成均匀分布,这时才与平行光照射时的等间隔条纹分布特征吻合.因此,在设计厚度不均匀薄膜的等厚干涉实验时,不能盲目地作平行光近似处理,应预先评估光源距离对条纹分布的影响,以减少实验系统误差.

4 结束语

劈尖干涉实验用点光源照射时,在劈尖表面有非均匀分布的干涉条纹,随光源距离增加,条纹间距逐渐变小,条纹变密,其中间距大的条纹比间距小的条纹减小幅度大,导致条纹间距随光源距离增大而趋于均匀,条纹间距也趋于稳定,当光源足够远时,条纹均匀分布,可等效为平行光干涉.

[1] 程路.薄膜干涉条纹的定域[J].大学物理,1982,1 (6):8-13.

[2] 陈冠英.薄膜干涉条纹定域的确定[J].大学物理, 1991,10(11):28-30.

[3] 刘金龙.劈尖干涉条纹定域的解析研究[J].物理与工程,2008,18(4):54-57.

[4] 程守洙,江之永.普通物理学[M].北京:高等教育出版社,1998:190-191.

[5] 赵新闻,黄生祥,周克省.对劈尖薄膜等厚干涉的讨论[J].广西物理,2005,26(4):44-46.

Distribution of wedge interference fringes with point light source

WANG Kai-sheng,ZHAO Zhi-min,YANG Yan-nan
(College of Science,Nanjing University of Aeronautics and Astronautics,Nanjing 211100,China)

An equation to determine the locations of the interference fringes appeared on the surface of a wedge near a point light source is deduced.The distribution of the interference fringes on the surface of the wedge is plotted by using numerical analysis method in Matlab.The impact of the distance between the wedge and the light source on the distribution of the interference fringes is discussed.

wedge interference;point light source;numerical analysis

O436.1

A

1005-4642(2010)01-0036-03

[责任编辑:郭 伟]

2009-04-17;

王开圣(1965-),男,江苏泰州人,南京航空航天大学理学院讲师,硕士,从事无损检测技术研究.

赵志敏(1954-),女,辽宁沈阳人,南京航空航天大学理学院教授,硕士,从事光测技术研究.