从时域和频域两种角度探讨卷积积分

杨永生, 赵梅

(苏州科技学院电子与信息工程学院,江苏苏州,215011)

0 引言

信号与系统是电气工程及其自动化、电子信息科学与技术以及通信信息工程等专业的专业基础课程,对后继课程的学习起到承前启后的作用[1-6]。在《信号与系统》这门课程中,主要从时域和频域两个角度分别来讲授确定性信号和线性时不变(LTI)系统的分析方法。在分析线性系统过程中,知道卷积运算将输入信号、输出信号以及冲激响应三者之间联系起来,主要有时域和频域两种计算方法。在时域法中,涉及到信号的平移、反转运算以及冲激响应的概念;而在频域法中,涉及到信号的傅里叶变换和频率响应的概念。可以看出,卷积运算将各种物理概念、分析方法以及知识点有机地衔接起来,是培养学生综合能力的一个重要方面。但是,在笔者多年的教学实践过程中,发现学生需要一个强化的学习过程才能够掌握卷积运算。要想真正理解卷积的物理含义及其应用,更是需要一个漫长的过程。为了能够保证学生运用卷积来解决工程实际问题,需要掌握扎实的理论基础。

1 时域法求解卷积

对任意两个信号f1(t)和f2(t),卷积的定义为：

为了方便起见,通常记作：

其中,“*”表示卷积运算。从式(1)可以看出,卷积是一种特殊的积分,它服从交换律、分配律和结合律。对信号来讲,其物理含义是可将任意的信号分解为无穷多个冲激信号之和,即：

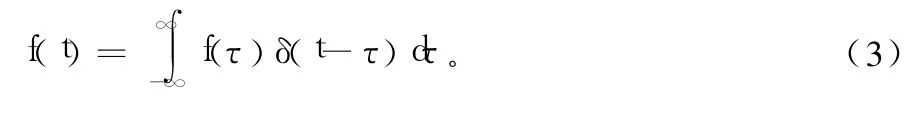
根据 LTI系统理论,若冲激响应为 h(t),输入信号 f(t),则系统的零状态响应 y(t)为：

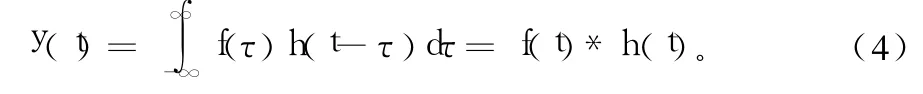
式(3)表明,输出信号可表示为输入信号与冲激响应的卷积。依据卷积的定义,可以看出,其计算步骤为,

① 将变量 t改为 τ,则信号的自变量为 τ,即 f1(τ)和f2(τ);

②将信号 f2(τ)反转,并作平移运算,其平移量为 t,得信号 f2(t-τ);

③将信号 f1(τ)与 f2(t-τ)相乘;

④对乘积项进行积分,积分限为 [-∞,∞],即 f(t)=

需要注意的是,步骤②信号f2(t-τ)的平移量 t决定信号 f1(τ)和信号 f2(t-τ)之间是否有重叠区域,如果有重叠区域,那么要确定步骤④中的积分上、下限,然后进行积分;如果没有重叠区域,则卷积为零。由于两信号在时间轴上的关系可分为部分重叠、完全重叠和无重叠三种情况,因此计算卷积的关键问题是找出两信号的重叠区域,确定积分上、下限。采用图解法可以直观地来说明卷积运算的全过程。对于两个有限长的信号 f1(τ)和 f2(-τ),如图 1所示。

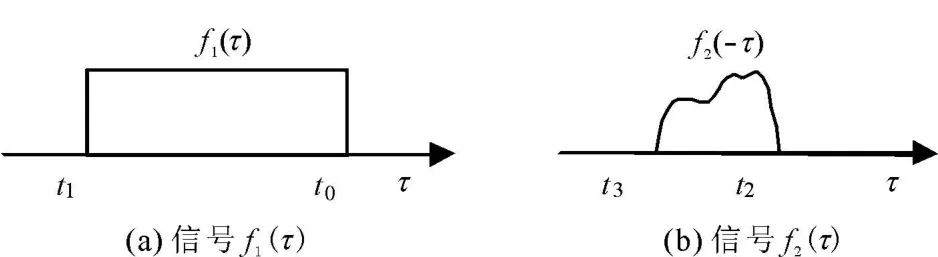
图 1 信号 f1(τ)和 f2(-τ)

随着平移量 t的不同,信号 f2(t-τ)在时间轴 τ的位置变化情况如图 2所示。当 t+t2＜t1时,信号 f2(t-τ)的前端还未进入信号 f1(τ)的末端,如图 2(a)所示。此时两信号没有重叠区域,卷积为零。当 t+t2＜t1且 t+t3＜t1时,信号f2(t-τ)的前端已进入信号 f1(τ)里,但信号 f2(t-τ)的末端还在信号 f1(τ)的外面,如图 2(b)所示。此时两信号是部分重叠,积分限为[t1,t+t2]。当 t+t3＞t1且 t+t2＜t0时,信号 f2(t-τ)全部进入信号 f1(τ)中,如图 2(c)所示。此时信号 f2(t-τ)完全进入信号 f1(τ)中,积分限为[t+t3,t+t2]。当 t+t3＜t0且 t+t2＞t0时,信号 f2(t-τ)的前端已部分移出信号 f1(τ)中,如图 2(d)所示。此时两信号是部分重叠,积分限为[t+t3,t0]。当 t+t3＞t0时,信号 f2(t-τ)的末端已移出信号 f1(τ),如图 2(e)所示。此时两信号没有重叠区域,卷积为零。

2 频域法求解卷积

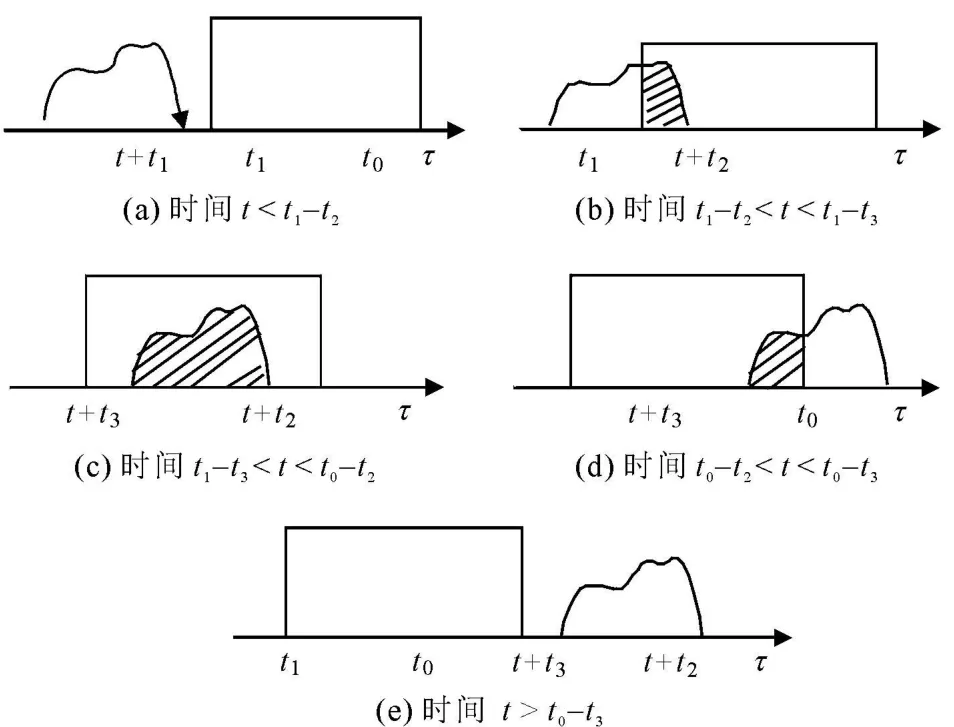
图 2 信号的卷积运算

对任意两个信号 f1(t)和 f2(t),若信号 f1(t)的Fourier变换记为 F1(jω),信号 f2(t)Fourier变换记为 F2(jω),则

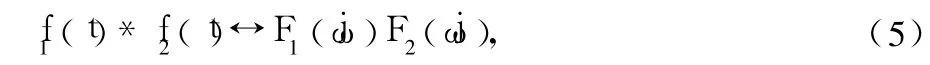
从式(5)可以看出,时域的卷积运算与频域的乘法运算相对应。众所周知,FFT是Fourier变换的一种快速算法,其运算量为logN。若信号 f(t)和 f(t)长度均为 N,则时域的212卷积运算量为 N2,而采用 FFT计算,其总的运算量为 2N+3Nlog2(2N)。表 1为时域法和频域法卷积运算量的比较。当N较大时,频域法的运算效率可提高一个数量级。

在分析 LTI系统时,结合式(4)和式(5),LTI系统的输出响应为：

式(6)是LTI系统的频域分析方法的理论依据,在滤波器的设计、频率响应的分析以及无失真传输等方面广泛应用。

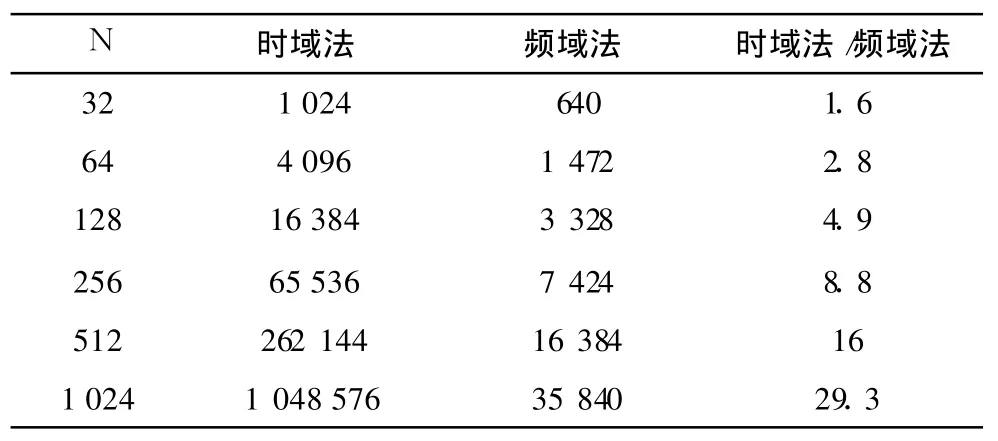
表 1 时域法和频域法卷积运算量的比较

3 结语

分析了时域法和频域法计算卷积的特点,并运用图示方法阐述时域法计算卷积积分的全过程,这有利于学生的学习和理解。但在实际工程中,由于该方法运算效率较低而未广泛采用,通常采用Fourier变换的方法来提高其运算效率。对于线性时不变系统来讲,激励信号、冲激响应以及输出信号是通过卷积运算相联系的。而在雷达和通信领域中的盲源分离、系统辨识以及信号估计等问题常遇到的是时变系统,因此快速解卷积算法需要进一步的研究。

[1]吴大正,杨林耀,张永瑞,等.信号与线性系统分析[M].第 4版.北京：高等教育出版社,2000.

[2]郑君里,应启珩,杨为理.信号与系统 [M].第 2版.北京：高等教育出版社,2000.

[3]丁玉美,高西全.数字信号处理[M].第 2版.西安：西安电子科技大学出版社,2001.

[4]孙贵根,杨冬云,李俊生.信号与系统[M].北京：机械工业出版社,2004.

[5]高秀英,吴长奇,王兰芳.基于匹配傅里叶变换的高动态载波捕获技术 [J].通信技术,2010,43(03)：19-20.

[6]盛广铭,吴中川,王甲峰.通信信号变采样率频域实现方法[J].通信技术,2010,43(02)：191-194.