对的积分方法探讨

陈浩

（宿州学院应用数学系，安徽宿州234000）

陈浩

（宿州学院应用数学系，安徽宿州234000）

通过对的积分方法的分析探讨，说明如何灵活使用积分法解决积分问题，方法灵活、巧妙，适用范围广。

积分；积分方法；形式逻辑；辩证逻辑

1 引言

数学分析主要研究的对象是变量与函数，它的主题是微积分，它所持的基本观点是运动的观点，变化的观点，所用的基本方法是极限的方法，用极限的思想贯穿于数学分析的始终，解决了函数的连续性、可微性、可积性等基本概

念和基本方法。它的内容既有形式逻辑，又有大量的辨证逻辑。一题多解能够巩固已学知识，开拓解题思路，探索解题技巧，训练解题的灵活性，增强解题能力，在比较各种解法的难与易，繁与简的基础上，能够总结出一些规律性的东西，进一步提高学习效果。

2 方法探讨

解法1：令x=asint，则dx=acostdt,所以

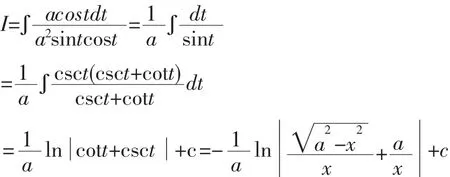
解法2：令x=asint，则dx=acostdt，所以

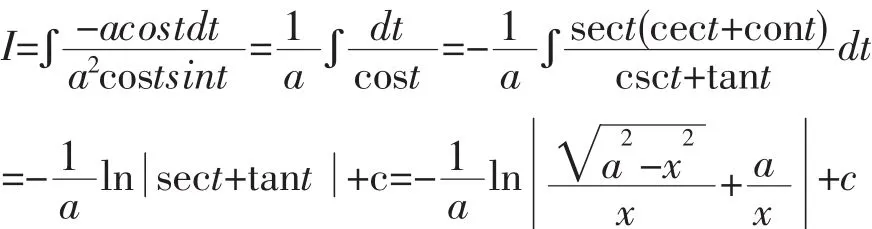
注：方法1和方法2是用传统的三角代换法将根号去掉，化为三角函数有理式的积分。[1，2]

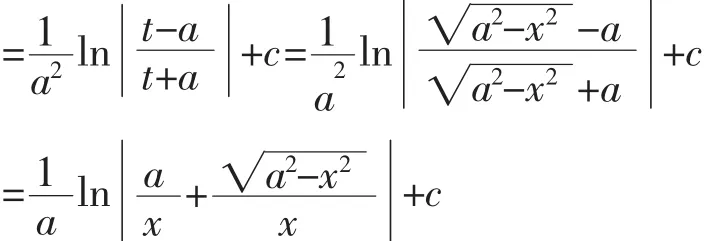
注：解法3利用x2+t2=a2中x与t的对称性，巧妙地将被积函数化为有理函数。

解法5：由解法4知

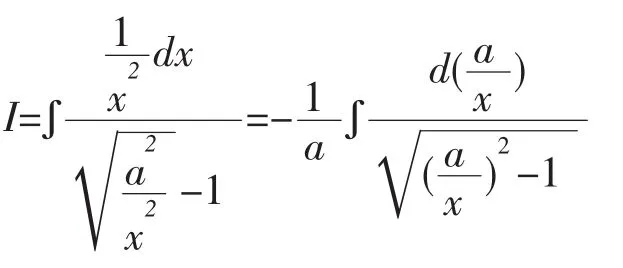
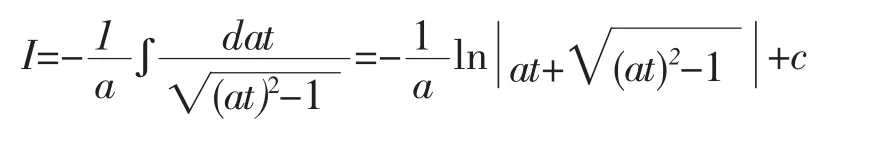
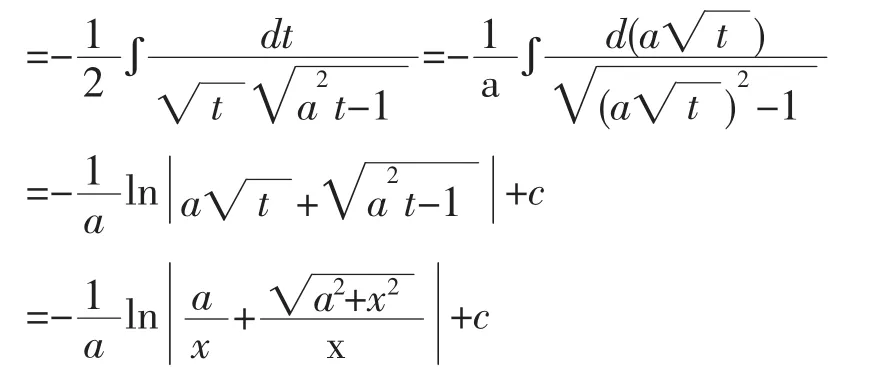
注：解法4-6是凑微分和第二换元法混合应用。

∴可令，则a+x=(a-x)t2

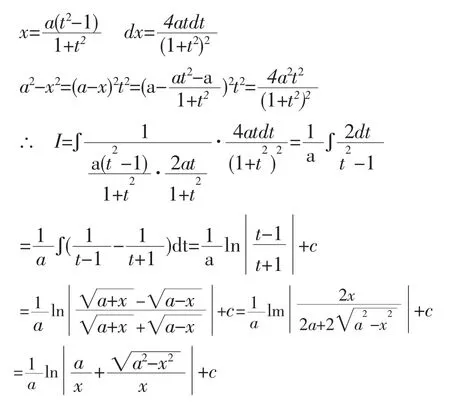
解法8：令,则a-x=(a+x)t2,

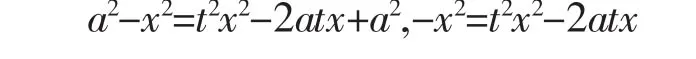
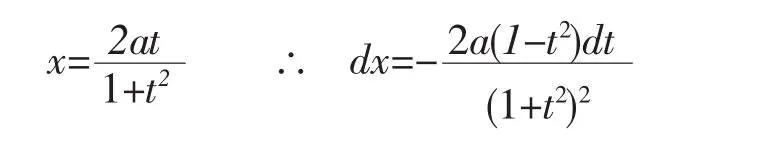
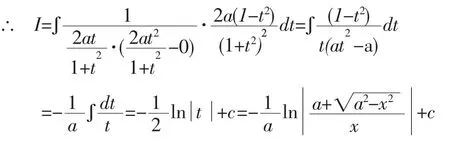
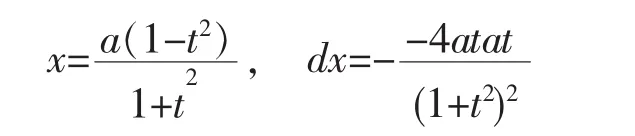
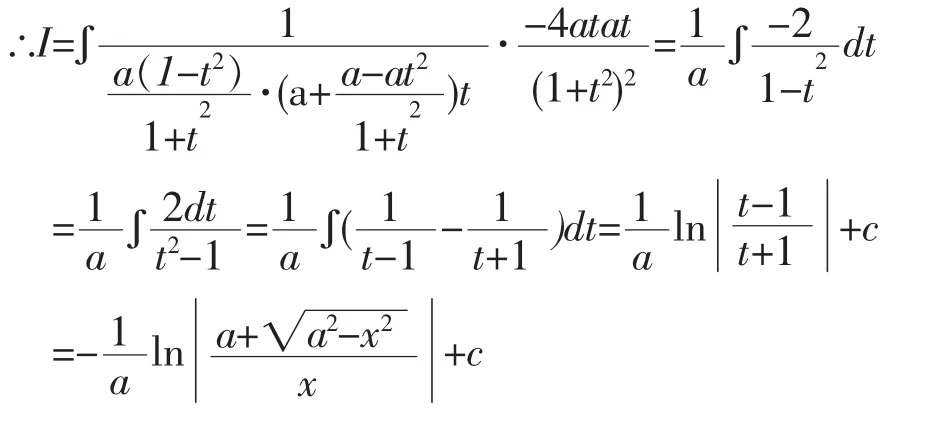
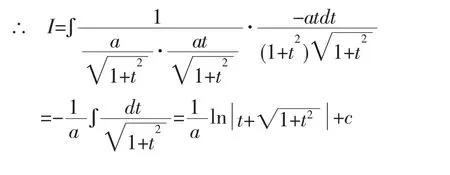
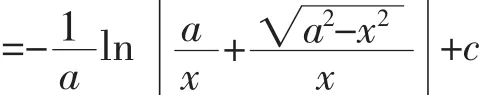
注：解法9-11是利用欧拉代换法。

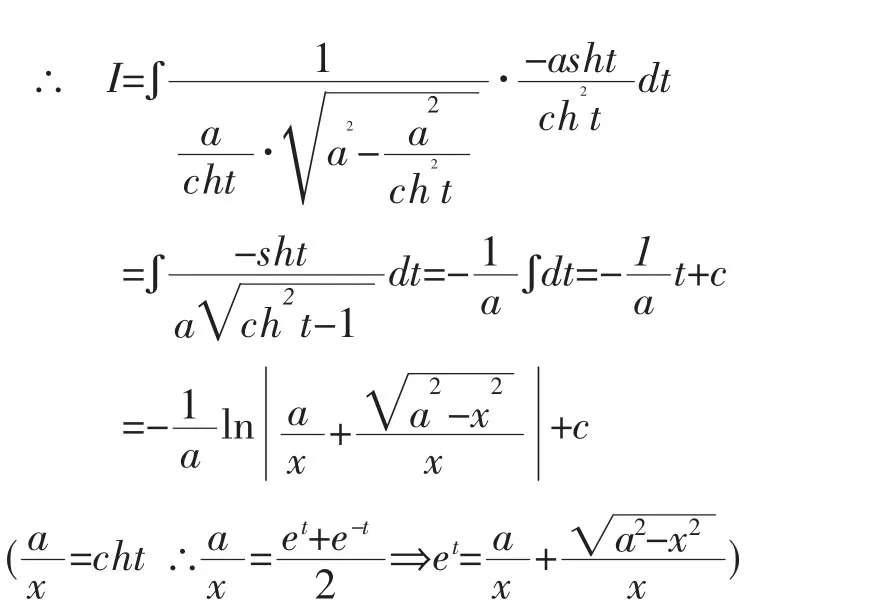
注:解法12利用了双曲余弦代换，简化了积分运算。

[1]华东师范大学数学系.数学分析[M].北京：高等教育出版社，1991:244-310.

[2]同济大学数学系.高等数学[M].北京：高等教育出版社，2004：198-210.

责任编辑：胡德明

Abstract:In this paper,integral method foris explored to show how to use the method to solve integration problems.It’s proved to be a flexible and ingenious method with wide applicability.

Key words:integral;integral method;formal logic;dialectical logic

Chen Hao
(Department of mathematics,Suzhou College,Suzhou 234000,China)

O172

A

1672-447X(2010)04-0007-03

2010-04-29

安徽省教育厅精品课程项目（安徽省教育厅教秘高[2006]53号）；宿州学院教授科研基金项目（2006jb08）

陈浩（1948-），安徽宿州人，宿州学院应用数学系教授，研究方向为泛函分析。