均匀带电细圆环电势的空间分布

马 堃，褚 园

(黄山学院信息工程学院,安徽黄山245021)

均匀带电细圆环电势的空间分布

马 堃，褚 园

(黄山学院信息工程学院,安徽黄山245021)

利用电势的定义式及电势的叠加原理，借助特殊函数论，导出了均匀带电细圆环电势的空间分布函数表达式，并借助Mathematica软件给出了电势与空间位置关系的二维和三维函数图像。

均匀带电圆环；电势分布；Mathematica

均匀带电细圆环周围空间电势和电场的分布是电磁学中经常研究的问题。[1-5]教材中，一般只给出在通过细圆环中心轴线上的电势和电场分布，对于全空间的分布讨论很少。[6,7]文献[4]直接由电场强度的计算公式计算了均匀带电细圆环在空间的电场分布，绘制出电场量值的空间二维分布图；文献[5]在柱坐标系中根据电场强度的计算公式，计算了均匀带电圆环在空间的电场分布，给出了级数形式解。本文将在直角坐标系中，直接利用点电荷的电势的计算公式及电势叠加原理，导出电势空间分布的函数表达式，并借助Mathematica计算软件，绘出电势与空间位置关系的二维和三维函数图像。

1 均匀带电细圆环的电势

如图1所示，设均匀带电细圆环的圆心为O，半径为R，电荷线密度为λ，如图建立坐标系，A是x轴上的一点，且OA=x，AB垂直于圆环所在的平面，AB=z，以无穷远处为电势零点，则B的电势可如下求解：将细圆环分割成无限多个小的线元，取P处一个小线元，其长度为dl=Rdθ，则该线元在的B电势可表示为

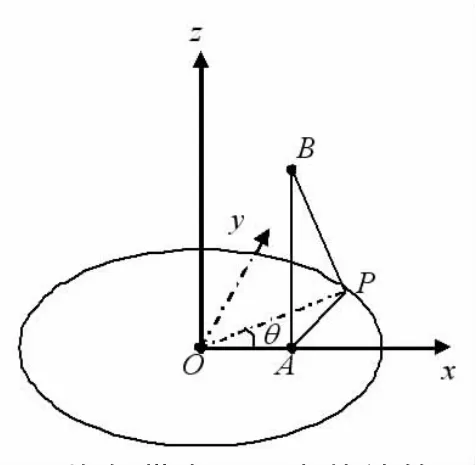
图1 均匀带电圆环电势计算用图

其中

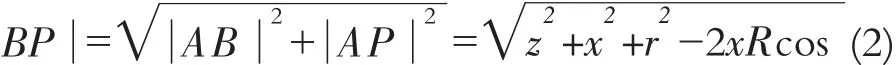
所以

令

则

再令

上式即为均匀带电细圆环电势的空间分布函数表达式，其中EllipticK表示第一类全椭圆积分，[8]即

2 讨论

2.1 均匀带电细圆环中心轴线上的电势

令(9)式中的x=0，从而得到均匀带电细圆环中心轴线上的电势分布函数，即

上式中Q是细圆环所带的总电量，这与教材给出的结论一样。[6,7]

利用Mathematica命令，可以作出均匀带电细圆环中心轴线上电势分布的二维函数图形，这里取λ/ε0=1及R=1，如图2。

图2 均匀带电圆环中心轴线上的电势分布

从图2可以看出，均匀带电圆环中心轴线上的电势呈对称分布，在z=0处，即在圆心处电势最强，两边电势对称递减。

2.2 均匀带电圆环所在平面上的电势

令(9)式中的z=0，从而得到均匀带点圆环在环面上任意点的电势分布函数，即

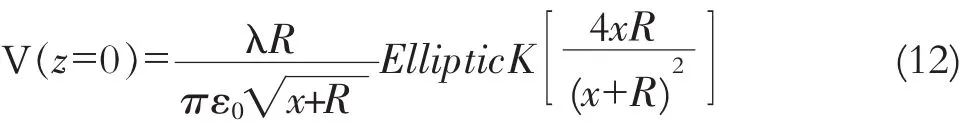
利用Mathematica命令，可以作出均匀带电细圆环所在平面上电势分布三维图形，这里取λ/ε0=1及R=1，如图3。

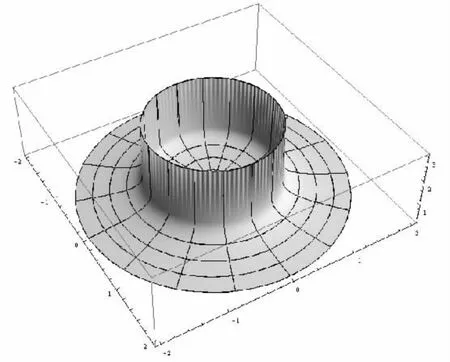
图3 均匀带电圆环所在平面上的电势分布

从图3可以看出，均匀带电圆环平面上的电势也呈对称分布，在处x=±1，即在细圆环上电势最强，两边电势对称递减。

2.3 均匀带电圆环空间的电势分布

利用Mathematica命令，作出均匀带点圆环空间的电势分布的三维函数图形，这里取λ/ε0=1及R=1,如图4。

图4 均匀带电圆环空间的电势分布

从图4可以看出，均匀带电圆环空间的电势分布情况：

1.在z=±1及x=0处出现极大值，即细圆环上的电势极大，以这两点为中心，整个空间电势呈对称分布；

2.在垂直于圆环所在平面轴线上的电势分布，以盘面为中心，对称分布，盘面处电势极大，两边对称递减;

3.圆环所在平面上的电势分布，以圆环为中心，对称分布，圆环上的电势极大，两边沿径向对称递减。

3 总结

本文在直角坐标系中，直接利用点电荷的电势的计算公式及电势叠加原理，给出电势空间分布的函数表达式，并借助Mathematica软件计算，绘出了电势与空间位置关系的二维和三维函数图像，所展现的推导过程简洁、易懂，给出的结果形象、直观。

[1]张连顺，姜万禄.环形线电荷的电场分布[J].大学物理,1998,17(8):21-23.

[2]张之翔.电磁学中几个简单问题里的椭圆积分[J].大学物理,2002,21(4):22-24.

[3]程昌林，王慧，李业凤.均匀带电细圆环的电场[J].大学物理,2003,22(6):15-17.

[4]周海英，陈浩.均匀带电细圆环的电场的一般分布[J].大学物理,2004,23(9):32-34.

[5]刘诚杰，刘景世.均匀带电细圆环电场的分布[J].大学物理,2005,24(8):19-20.

[6]贾起民，郑永令，陈暨耀.电磁学(第二版)[M].北京：高等教育出版社，2001：31-32.

[7]黄时中.大学物理学(下册)[M].合肥：中国科学技术大学出版社，2006：29.

[8]王竹溪，郭敦仁.特殊函数概论[M].北京：北京大学出版社，2000:524-526.

责任编辑：胡德明

Abstract:Based on the definition and the superposition theorem of electric potential and aided by the theory of special functions,the function expression of the electric potential distribution of uniformly charged rings has been obtained.The two-dimensional and three-dimensional diagrams for electric potential and spatial relation have been plotted by Mathematica.

Key words:uniformly charged ring;electric potential distribution;Mathematica

The Electric Potential Distribution of Uniformly Charged Rings

Ma Kun,Chu Yuan
(School of Information Engineering,Huangshan University,Huangshan 245021,China)

O441.1

A

1672-447X(2010)04-0025-03

2010-03-26

黄山学院教学研究项目(2008hsujy010);黄山学院自然科学研究项目(2008xkjq013)

马堃(1983-),安徽六安人,黄山学院信息工程学院教师,硕士。