（1+1+1）维时空光孤子控制

郝瑞宇，琚爱堂

（长治学院 电子信息与物理系，山西 长治 046011）

（1+1+1）维时空光孤子控制

郝瑞宇，琚爱堂

（长治学院 电子信息与物理系，山西 长治 046011）

本文通过数值地求解孤子控制系统下的（1+1+1）维非线性薛定谔方程，讨论在一定的孤子控制系统中传输的时空光孤子。结果表明，在一定的孤子控制系统中，（1+1+1）维时空光孤子可较稳定地传输。最后，讨论时空光孤子传输过程的稳定性。结果表明，在白噪声扰动下，时空光孤子传输过程是稳定的。

孤子控制；时空光孤子；（1+1+1）维；非线性薛定谔方程

1 引言

作为光学非线性波相互作用研究领域中的主要内容之一，时空光孤子的产生已成为当前的研究热点。时空光孤子，实际上是局域在横向空间和时间的光脉冲，对于它的研究已有一些成果。如Sil berberg等在Kerr光学介质中考虑了这样的光脉冲，并称之为“光弹”。“光弹”实际上强调的是它的类粒子性。而对于这样的“光弹”的形成，可以理解为是线性和非线性作用平衡的结果。或者说是衍射、群速度色散、自聚焦、非线性相位调制效应相互平衡的结果[1]。

在理论上，描述时空光孤子的模型方程可以是非线性薛定谔方程［1］：

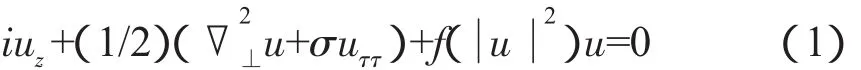
在方程中，z是传输距离，τ=t-z/Vgr，是由群速度重新度量的时间，其中，Vgr是波的群速度，σ是依赖于载波波长的群速度色散系数，▽2⊥代表横向衍射，（f u2）描述介质有效折射率的非线性修正。如果考虑Kerr效应，则 （f u2）=K（u2），K 是常数。

另一方面，近年来，孤子控制是孤子应用方面的一个新的发展。孤子控制可由变系数非线性薛定谔方程描述[2-5]。考虑到时空光孤子的孤子控制，方程（1）可变为［1］：

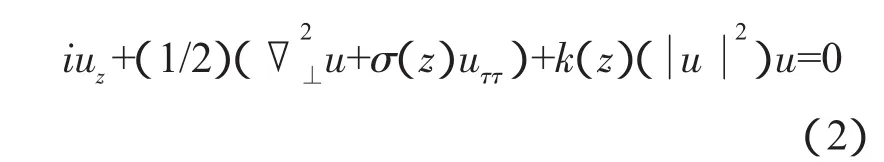
其中 σ（z），k（z）都是传输距离 z的函数。人们可选取它们不同的形式，得到各种不同的孤子控制。

如果只考虑（1+1+1）维时空光孤子控制，则方程（2）也可变为：

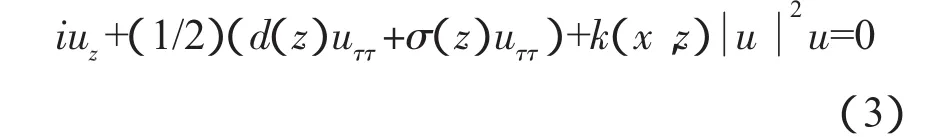
本文将通过数值求解方程（3），讨论（1+1+1）维时空光孤子控制。

2 数值分析

我们取孤子控制系统：

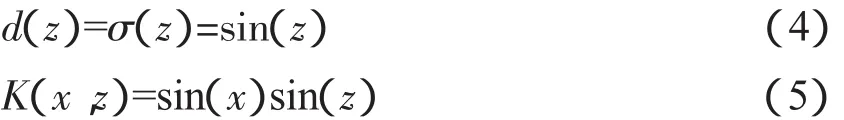
和初始光：

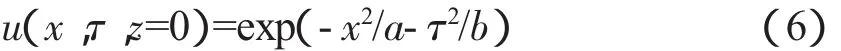
则可以形成如图1（a）、图1（b）、图1（c）所示的稳定的时空光孤子传输。当然，从图中也能看到，图1（b）表示的z=20处的时空光孤子和初始光比较，稍有变形，但到了图1（c）表示的z=50处的时空光孤子，则基本回到原状。

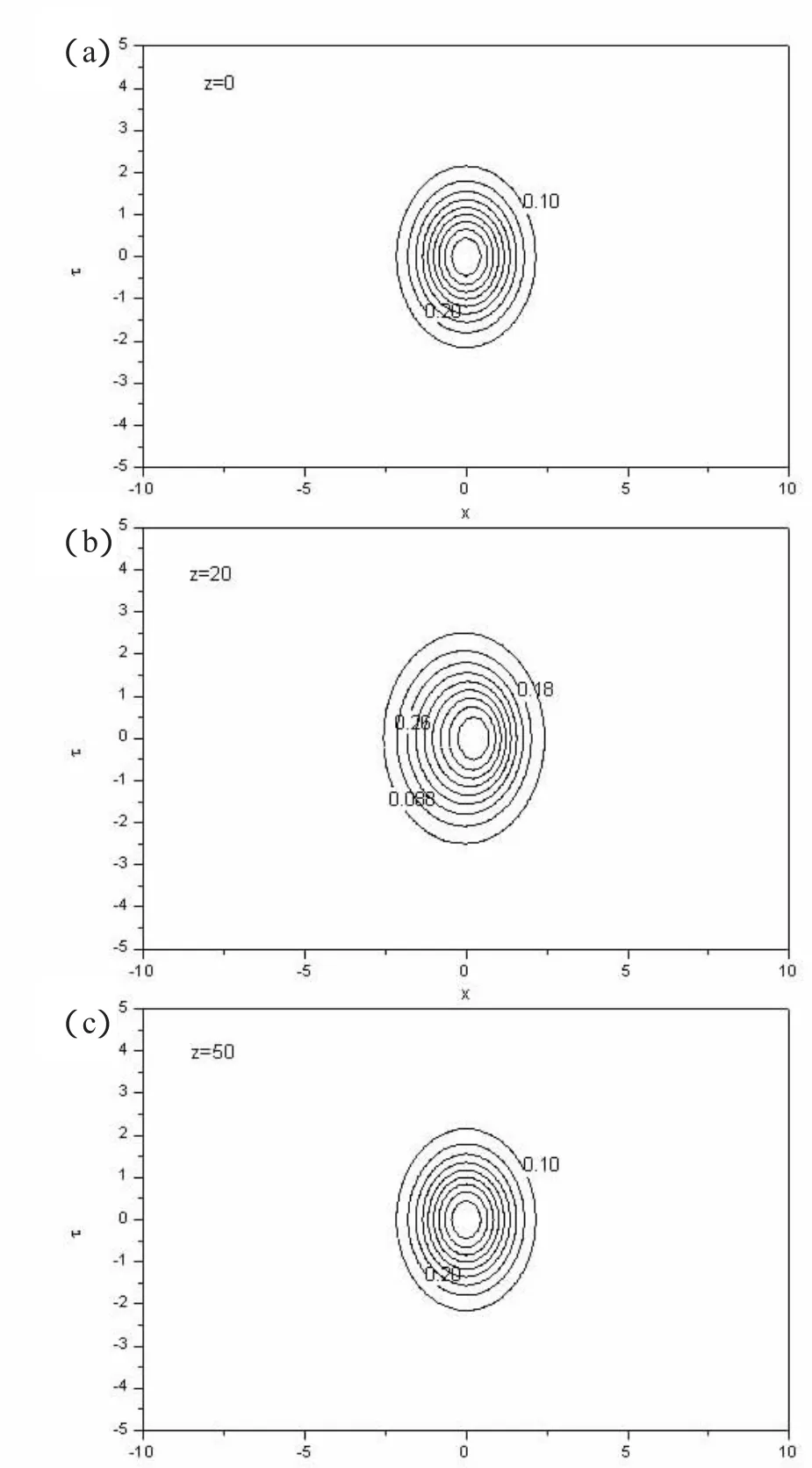
图1 由（4）和（5）给定的控制系统中光脉冲传输图Fig1 The propagation plot of optical pulsewith the input form（6）in nonlinear system（4）and（5），here the parameters adopted are：.

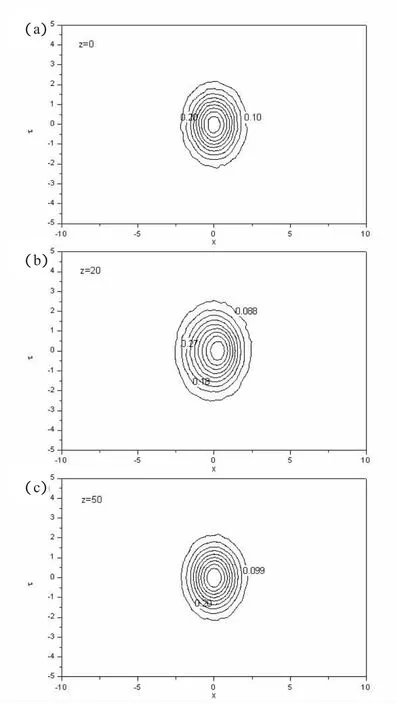
图2 白噪声扰动下光脉冲传输图Fig 2 The propagation plotof optical pulse under the perturbation ofwhite noisewhosemaximal value is 0.01.

另外，这样的稳定的时空光孤子传输具有较好的稳定性。如在有限的初始振幅扰动，白噪声扰动下，仍能保持稳定的光孤子传输。图2（a）、图2（b）、图2（c）描述了白噪声扰动下的光孤子传输过程。与图1比较，可以看出，图2保留了（1+1+1）维时空光孤子传输的主要特征，即在文中给定的孤子控制系统下，时空光孤子传输过程是稳定的。

3 结论

通过数值求解在孤子控制系统下的（1+1+1）维非线性薛定谔方程，讨论了在孤子控制系统中的时空光孤子传输。结果表明，在一定的孤子控制系统中，（1+1+1）维时空光孤子可较稳定地传输。最后，讨论了时空光孤子传输过程的稳定性。结果表明，在白噪声扰动下，时空光孤子传输过程是稳定的。这些结果对今后更多的物理解释与应用是有用的。

［1］B.A.Malomed，D.Mihalache，F.W ise，L.Torner.Spatiotemporal optical solitons［J］.J.Opt.B：QuantuMSeMiclass.Opt.2005，7（5）：R 53-R72.

［2］V.N.Serkin and A.Hasegawa.Exactly Integrable Nonlinear Schr？dinger Equation Models W ith Varying Dispersion，Nonlinearity and Gain：Ap-plication for Soliton Dispersion Managements［J］.IEEE Journal of Selected Topics In QuantuMElectronics，2002，8（3）：418-431.

［3］V.I.Kruglov，A.C.Peacock and J.D.Harvey.Exact Self-Similar Solutions of the Generalized Nonlinear Schr?dinger Equation w ith Distributed Coefficients［J］.Phys.Rev.Lett.2003，90（11）：113902（1-4）.

［4］R.Y.Hao，L.Li，Z.H.Li，W.R.Xue and G.S.Zhou.A new approach to exact soliton solutions and soliton interaction for the nonlinear Schr?dinger equation w ith variable coefficients［J］.Opt.Commun.2004，236（1-3）：79-86.

［5］R.Y.Hao，L.Li，Z.H.Li，R.C.Yang and G.S.Zhou.A new way to exact quasi-soliton solutions and soliton interaction for the cubic-quintic nonlinear Schr？dinger equation w ith variable coefficients ［J］.Opt.Commun.2005，245（1-6）：383-390.

Abstract：In this paper,we investigate（1+1+1）-dimensional nonlinear Schr？dinger（NLS）equation with soliton control,which describes the propagation of spatiotemporal optical solitons in soliton control system.The results reveal that the propagation of spatiotemporal optical solitons can be stable in the soliton control system.Finally its stability is also analyzed.The results show that the propagation is stable to the finite initial perturbations,such aswhite noise.

Keywords：soliton control；spatiotemporal optical soliton；（1+1+1）-dimensional；the nonlinear Schr？dinger equation

（责任编辑 王璟琳）

（1+1+1）-Dimensional SpatioteMporal Optical Soliton Control

HAO Rui-yu，JU Ai-tang
（Department of Electronic Information and Physics，Changzhi University，Changzhi Shanxi046011）

TN929.1

A< class="emphasis_bold">文章编号：1

1673-2014（2010）02-0001-03

2010—03—01

山西省青年科技研究基金（2008012002-2）资助

郝瑞宇（1979— ），男，山西阳泉人，博士，副教授，主要从事光孤子理论研究。