利用推广的(G′/G)展开法求解BBM方程

2010-09-11邢秀芝曹桂文

周口师范学院学报 2010年5期

关键词：双曲行波方程

邢秀芝,曹桂文

邢秀芝1,曹桂文2

(1.周口师范学院数学系,河南周口466001;2.商丘职业技术学院数学团队,河南商丘476100)

利用推广的(G′/G)展开法,借助于计算机代数系统Mathematica,获得了BBM方程的丰富的显式行波解,分别以含两个任意参数的双曲函数、三角函数及有理函数表示.

BBM方程;推广的(G′/G)展开法;显式行波解;齐次平衡法

构造非线性发展方程的精确解是非线性科学的一个重要组成部分,也是长期以来物理学家和数学家研究的重要课题.人们为了得到非线性发展方程的精确解提出了许多有效的方法.常用的方法有齐次平衡法[1]、双曲正切函数法[2]、椭圆函数展开法[3]、扩展的双曲正切函数法[4]等.

最近,文献[5]中新提出了(G′/G)展开法,这里的G=G(ξ)是一个二阶线性ODE的解.该法的主要思想是:非线性发展方程的行波解可以表示为(G′/G)的多项式,多项式的次数可由齐次平衡原则确定;多项式的系数可通过解一个非线性代数方程组求得;非线性代数方程组是在应用(G′/G)展开法过程中产生的.应用该方法已有效地求解了许多非线性演化方程[6-8].文献[9]将(G′/G)展开法从正幂展开推广到正负幂展开,并用它获得了 KD方程较文献[7]丰富的显式行波解.本文应用推广的(G′/G)展开法求解BBM方程

获得了方程(1)的含两个任意参数的更多的显式行波解,其结果丰富了以往文献.为求解方程(1),令

将(2)式代入(1),对ξ积分一次并令积分常数为零,得到关于u=u(ξ)的常微分方程

考虑方程(3)中最高阶导数项u″与最高次非线性项u2的齐次平衡,可确定平衡数N=2.因而可设方程(3)的解为

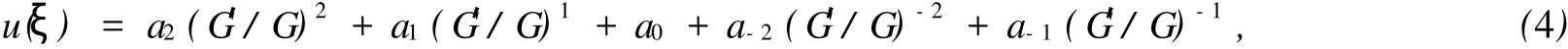
其中 a2,a1,a0,a-1,a-2为待定常数,G=G(ξ)满足二阶线性常微分方程

将式(4)代入式(3),并利用方程(5),合并(G′/G)的同次幂系数,并置其为零,得到关于 a2,a1,a0,a-1, a-2,ω,λ,μ的代数方程组

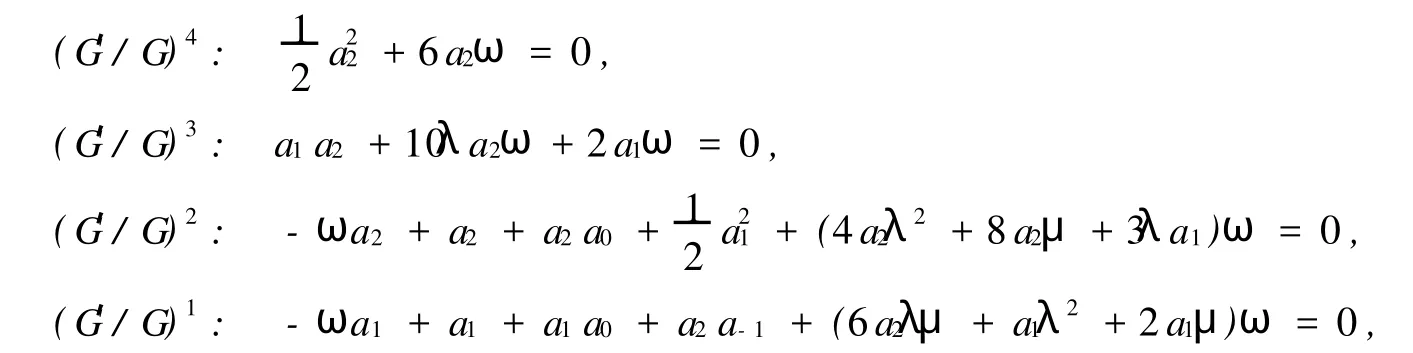
借助于计算机代数系统Mathematica得到6组解:将以上结果代入式(4)得BBM方程的以下几种类型的显式行波解.

1)当λ=0且μ<0时,BBM方程有双曲函数解:

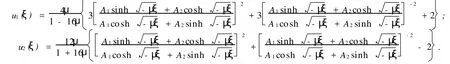
2)当λ2-4μ>0时,BBM方程有双曲函数解:

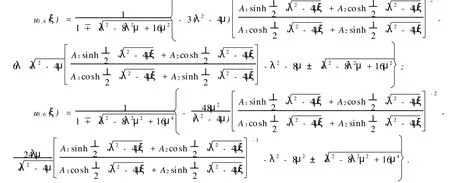
3)当λ=0且μ>0时,BBM方程有三角函数解:5)当λ2-4μ=0时,BBM方程有有理函数解

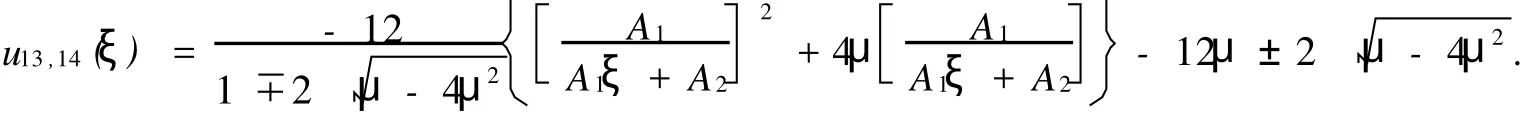
其中以上各式中的A1,A2均为任意参数.

[1]范恩贵,张鸿庆.非线性孤子方程的齐次平衡法[J].物理学报,1998,47(3):353-362.

[2]扎其劳,斯仁道尔吉.修正双曲函数法与非线性发展方程的精确解[J].内蒙古师范大学学报:自然科学汉文版,2007, 36(1):15-21.

[3]刘式适.Jacobi椭圆函数展开法及其在求解非线性波动方程中的应用[J].物理学报,2001,50(11):2068-2073.

[4]Fan Engui.Extended tanh-function method and its applications to nonlinear equations[J].Physics Letters A,2000,277: 212-218.

[5]Wang M L,Zhang J L,Li X Z.The(G′G)2 expansion Method and Travelling Wave Solutions of Nonlinear Evolution Equations inMathematical Physics[J].Phys LettA,2008,372(4):417-423.

[6]Zhang S,Tong J L,WangW.A Generalized(G′G)expansionMethod for the mKdV Equation with Variable Coefficients [J].Phys LettA,2008,372(13):2254-2257.

[7]Ahmet Bekir.App lication of the(G′G)expansionMethod for Nonlinear Evolution Equations[J].Phys Lett A,2008, 372(19):3400-3406.

[8]Zhang J,Wei X L,Lu Y J.A generalized(G′G)expansionMethod and its App lications[J].PhysLettA,2008,372 (20):3653-3658.

[9]李灵晓,李保安.利用推广的(G′/G)展开法求解 Kononpe lchenko-Dubrovsky方程[J].河南科技大学学报:自然科学版,2009,30(1):75-77.

Solving BBM equation by using extended(G′/G)expansion method

XING Xiuzhi1,CAO Guiwen2
(1.Department of Mathematics,Zhoukou Normal University,Zhoukou 466001,China; 2.Mathematics Teaching Team,Shangqiu Polytechnic,Shangqiu 476100,China)

By using the extended(G′/G)expansion method and with the aid of computer algebra system Mathematica,abundant exact travelling wave solutions of the BBM equation were successfully obtained.The solutions were expressed by hyperbolic functions,trigonometric functions and rational functions contained double arbitrary parameters.

BBM equation;extended(G′/G)expansion method;exact travelling wavesolution;homogeneous balance

O175.2

1671-9476(2010)05-0023-03