光学玻璃磨削机理的仿真研究*

沈琳燕 李蓓智 杨建国

（东华大学机械工程学院，上海 201620）

光学玻璃磨削机理的仿真研究*

沈琳燕 李蓓智 杨建国

（东华大学机械工程学院，上海 201620）

采用有限元仿真分析方法，利用有限元增量理论建立了玻璃材料的弹塑性本构关系，对单颗金刚石磨粒的磨削过程进行了仿真，最后从最大拉应力、磨削力、磨削力比3个方面对仿真结果进行了分析研究，为玻璃磨削加工的工艺参数优化和工艺规划奠定了基础。

高速磨削 光学玻璃 仿真 磨削力

随着尖端科学技术的不断发展，高质量的玻璃等脆性材料产品的需求大大增加。因此，需要对它们进行精密及超精密加工。这些材料虽然用处十分广泛，但其硬度高，脆性大，其物理机械性能尤其是韧性和强度与金属材料相比有很大差异。由于玻璃等脆性材料在韧性和强度方面相互之间差异较大，所以玻璃材料的磨削既不同于一般高脆性材料（如金刚石）的纯断裂过程，又不同于金属材料的塑性剪切过程。为了获得高质量的玻璃材料产品，现在一般采用研抛技术加工，但研抛技术生产周期长，产品成本高。近年来，超精密磨削技术的进步，使得磨削表面的质量等同甚至优于研抛表面［1，2］，并且加工效率得以大幅度提高。因此，研究玻璃等脆性材料超精密磨削过程中的磨削特性是很有必要的，这将对脆性材料的超精密加工提供一定的科学参考价值。

由于实际加工过程中的切削温度、应力、应变等的测量极其困难，单纯依靠实验很难对磨削机理进行深入的研究。计算机仿真方法能够揭示实验很难获得的物理力学现象，从而为深入研究磨削机理奠定基础。因此本文从仿真角度对单颗金刚石磨粒磨削玻璃进行机理研究，通过分析单颗磨粒的理想磨削过程，建立了单颗磨粒磨削的仿真模型。基于该模型，利用有限元软件对不同磨削条件下的磨削过程进行仿真，分析了砂轮线速度、磨削深度同应力、磨削力之间的关系，并得出磨削过程中玻璃的变形，进而可对磨削过程的参数进行优化，使磨削过程的研究更加快捷、有效［3］。

1 有限元分析模型

1.1三维几何模型的建立

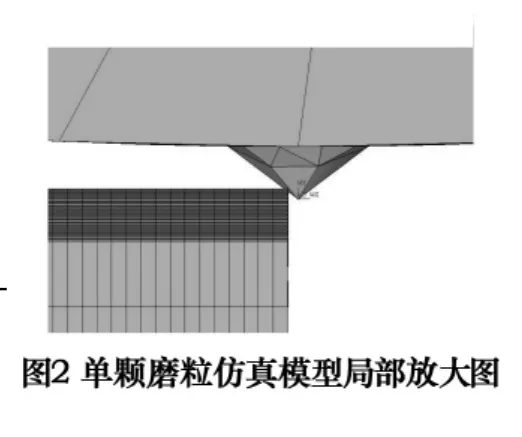
用于切削仿真的数值模拟计算方法主要有两种，即欧拉方法及拉格朗日方法。欧拉方法中有限元网格描述空间域，材料可以在网格间流动。欧拉方法可以模拟稳态切削过程，但无法模拟切屑的形成。拉格朗日方法是固体分析方法，有限元网格紧紧贴在材料上，随着工件的变形而变形，此方法可以模拟切屑的形成，但必须定义切屑的分离准则。本文采用拉格朗日方法建立了玻璃三维磨削的有限元模型，如图1所示。其中工件以速度vw沿x轴正方向运动，砂轮以线速度vs沿z轴顺时针旋转。切屑分离准则采用物理量分离准则，即单元节点分离，充分采用网格划分工具MeshTool对砂轮划分网格，采用智能单元尺寸控制方法对工件划分网格，磨粒附近应力和应变都集中的材料部分，采用较密的网格划分，在远离磨粒的地方采用较大尺寸的网格单元。如此划分网格后，既可以获得足够的计算精度，又可以节省计算时间。

对磨削区的应力分析建模是一个技巧性的问题。如果将其作为一个动力学问题，考虑工件的惯性和加速度，则工件的质量是一个未知数，而且也不能反映磨削过程的现象。通过分析比较发现，根据相对运动原理，假设工件不动，砂轮磨粒相对工件切削层作挤压运动，最终形成切屑脱离，用非线性接触问题建模，不但符合实际切削过程，而且有利于数值计算，可以较好地模拟磨削过程。通过将砂轮磨粒定义为“接触面”，工件切削层定义为“目标面”，建立了一个接触分析中的Eroding（ESTS）接触，假设目标面固定不动，接触面（即砂轮磨粒）相对目标面作一个微小的位移，这样就使目标面产生了一个挤压变形产生切屑的过程，据此，可以建立有限元模型进行应力分析。如图1、2所示，砂轮尺寸为φ100 mm×5 mm，单颗磨粒形状抽象为顶锥角为106°的理想圆锥［4］。将工件简化为长7 mm，宽6 mm，高3 mm的矩形，底面和侧面都固定。玻璃材料在微量切削条件下呈塑性，材料力学性能服从双线性随动强化假设，根据文献［5］提供的数据，玻璃的剪切模量G=30.4 GPa，最大抗拉强度 T=0.15 GPa，Hugoniot弹性极限为5.95 GPa。

1.2 工件材料本构模型的建立

材料的本构关系反映了材料物质本性的变化，是任何有限元建模仿真过程的关键环节和成败的关键因素。超精密磨削脆性材料时存在断裂模式、断裂与塑性模式、塑性模式，磨粒的磨削深度值小于脆塑转变的临界值，光学玻璃处于塑性模式磨削状态，磨削后的表面没有任何微裂纹缺陷［6］。利用有限元增量理论建立磨削加工的材料本构关系，考虑到磨削加工过程中的损伤情况，采用Johnson_Holmquist_Ceramics塑性模型。该模型对于建立陶瓷、玻璃等脆性材料的本构关系非常有效［7～9］。其等效应力如下：

由JH模型得出塑性应变增量关系：

式中：A、B、C、m、n、d1、d2为 JH 模型的材料参数;p 为应力。

2 磨削过程仿真及其结果分析

单颗磨粒以一定的速度与工件发生作用，在磨削区发生了复杂的物理、化学变化，工件产生了非线性的弹塑性变形。ANSYS/LS－DYNA显示动力分析模块是功能齐全的非线性显示程序分析包，可以模拟各种复杂的非线性动态过程，求解各种几何非线性、材料非线性和接触非线性问题［10］。在ANSYS环境下完成仿真模型建立、网格划分、载荷施加等工作，然后利用LS－DYNA求解器进行求解和后处理，最后得到仿真结果。

2.1 仿真求解

磨粒材料模型选择金刚石。金刚石磨粒具有硬度高、强度好、颗粒形状好、磨削能力强、导热性能佳、热膨胀系数小等特点，是理想的磨削材料［11］，适合加工硬而脆的材料，在磨削加工领域得到了广泛的应用。因此选择金刚石磨粒作为仿真的材料模型对于理论研究和实际应用都具有重要意义。

工件材料模型选择玻璃。参考相关手册，取仿真模型中砂轮直径为100 mm，磨粒高度为0.05 mm，根据表1的参数范围，仿真得到不同磨削条件下的结果。

表1 仿真参数

2.2 磨削深度的影响

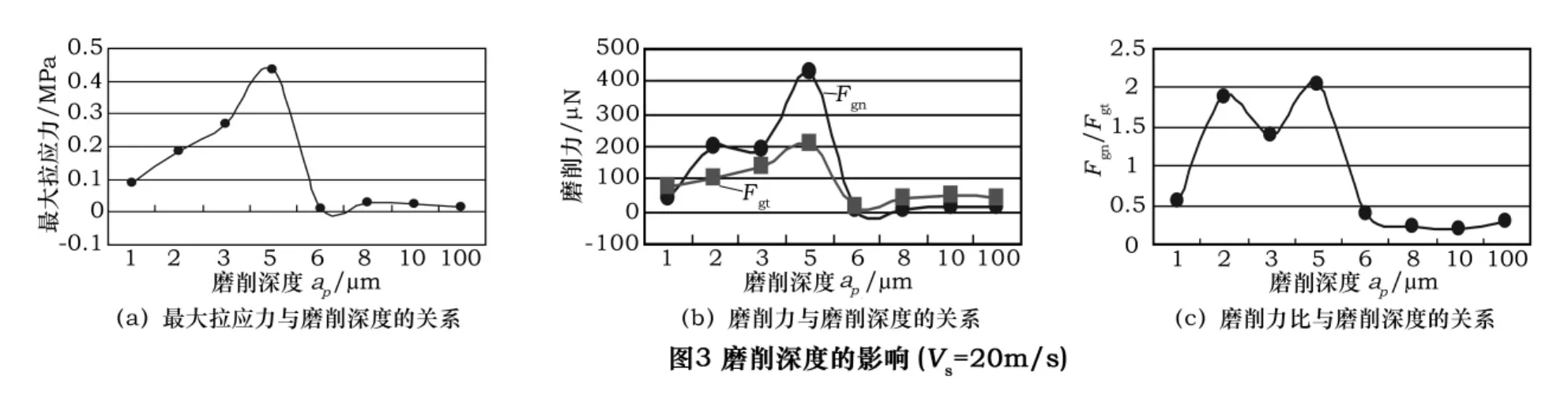
图3为砂轮线速度和工件进给速度一定时，最大拉应力、磨削力、磨削力比随磨削深度的变化曲线。在砂轮线速度20 m/s情况下，磨削深度ap在1～5 μm区间时最大拉应力、磨削力及磨削力比基本随磨削深度的增加呈递增规律，且磨削深度在1 μm左右时，其值最小，此时工件表面质量最好，和文献［6］结果相对应。

当磨削深度ap≤5 μm时，磨削表面上方的待去除材料很少，磨粒刃口半径和磨削深度相当，消除了应力集中，整个磨削区处于高静压状态，此时磨粒刃附近的应力状态均布与高静压试验时的应力状态相似，脆性材料的塑性增强，材料以塑性变形的方式被切除掉，脆性材料经磨削加工就可以得到较好的表面质量。而当磨削深度ap>5 μm时，在极锋利的磨粒刃附近的拉应力区产生高度应力集中状态，而磨削表面上方的大部分待去除材料处于小应力状态，由于玻璃的断裂韧度低，当砂轮向前作切削运动时，裂纹会立即在磨粒刃前产生，而不会产生塑性变形，此时加工表面产生凹坑，材料以脆性断裂方式去除，故应力值突然减小并趋于零。

2.3 砂轮线速度的影响

图4是砂轮线速度与最大拉应力、磨削力之间的关系曲线。当磨削深度和工件速度一定时，随着砂轮线速度的提高，最大拉应力、磨削力基本呈递减规律。

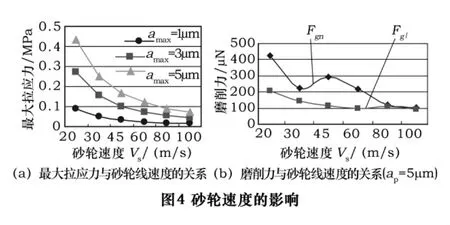
砂轮线速度提高时，未变形切屑厚度减小，切屑层厚度变薄，导致磨粒刃口半径和切削层厚度相当，消除了应力集中，脆性材料的塑性增强，最大拉应力、磨削力随之减小，材料以塑性变形的方式被切除掉，这表明砂轮线速度提高可以显著改善工件表面的应力状况，提高表面质量。

3 结语

（1）采用有限元软件模拟脆性材料磨削加工过程，分析加工后已加工表面所产生的最大拉应力、磨削力及磨削力比，可避免脆性材料的试切加工，大大提高研究的效率，降低研究的成本，同时也弥补了磨削力、应力在线检测手段的不足，为认识脆性材料的磨削机理提供了有力的途径。

（2）对脆性材料磨削表面进行应力、力的分析是一个非线性问题，而基于Johnson_Holmquist_Ceramics理论的弹塑性有限元方法是其有效的解决方法。

（3）分析了最大拉应力、磨削力与砂轮线速度及磨削深度之间的关系，最大拉应力随砂轮线速度的增加而减小，磨削力随砂轮线速度的增加基本上呈递减规律，但递减速率变小;最大拉应力、磨削力基本随磨削深度的增加呈递增规律，但存在一个临界最大值，当磨削深度超过临界值时，脆性材料发生脆性断裂，最大拉应力、磨削力突然下降趋于零。

1 Yoshiharu NAMBA，Morihiko SAEKi，Takatomo SASAKI.Ultra－precision Grinding of KTP Crystals for Optical Surfaces［J］.Int.J.Japan Soc.Prec.Eng.，1994，28（1）：39－40

2 Mochida S，Kubo K，Nagano H.Flexible Manufacturing System for Spherical Glass Lenses［J］.National Tech.Rept.，1990（36）：172 －180

3 刘媛，张勤俭，叶书强等.聚晶金刚石复合片硬质合金层磨削过程数值模拟［J］.系统仿真学报，2006（8）：529～532

4 王德泉.砂轮特性与磨削加工［M］.北京：中国标准出版社，2001：27～29

5 王承遇，陶瑛.玻璃材料手册［M］.北京：化学工业出版社，2008：478～491

6 陈明君，张飞虎，董申等.光学玻璃塑性模式超精密磨削加工的研究［J］.中国机械工程，2001，4（12）：460 ～462，484

7 LS－DYNA KeyWord User’s Manual（VOLUME I），LIVERMORE SOFTWARE TECHNOLOGY CORPORATION（LSTC），2007（5）：415－417

8 Duane S.Cronin，Khahn Bui，Christian Kaufmann.Implementation and Validation of the Johnson－Holmquist Ceramic Material Model in LSDyna.4thEuropean LS－DYNA Users Conference.2004：D－I－47－59

9 HOLMQUIST，T.J.，JOHNSON，G.R.，GRADY，D.E.，LOPATIN，C.M.and HERTEL，E.S.（1995），“High strain rate properties and constitutive modeling of glass”，Proceedings of Fifteenth International Symposium on Ballistics，Jerus a － lem，Israel，May 1995

10 尚晓江，苏建宇.ANSYS/LS－DYNA动力分析方法与工程实例［M］.北京：中国水利水电出版社，2006.

11 李伯民，赵波.现代磨削技术［M］.北京：机械工业出版社，2003：414

如果您想发表对本文的看法，请将文章编号填入读者意见调查表中的相应位置。

Simulation Study of Optical Glass Grinding Mechanism

SHEN Linyan，LI Beizhi，YANG Jianguo
（School of Mechanical Engineering，Donghua University，Shanghai 201620，CHN）

In this paper，elastic－plastic constitutive relation of glass was established by the use of finite element incremental theory，and the single－grit diamond grinding process was simulated.The simulation results were analyzed from the aspects of the maximum tensile stress，grinding force and grinding force ratio，which laid a foundation for process parameters optimization and process planning for grinding optical glass.

High Speed Grinding;Optical Glass;Simulation;Grinding Force

* 上海市重点学科建设项目资助（B602），国家973计划项目资助（2009CB724403）

沈琳燕，女，1984年生，硕士研究生，研究方向为脆性材料磨削机理研究。

p

2009－07－03）

10229