利用固相能量守恒定律判定煤炭最短发火期

朱云辉,程功林,方良才,夏仕伯

(1.淮南职业技术学院通风安全系,安徽淮南 232001;2.淮南矿业 (集团)有限责任公司安全开采总院,安徽淮南 232001)

利用固相能量守恒定律判定煤炭最短发火期

朱云辉1,程功林1,方良才2,夏仕伯2

(1.淮南职业技术学院通风安全系,安徽淮南 232001;2.淮南矿业 (集团)有限责任公司安全开采总院,安徽淮南 232001)

利用固相能量守恒定律判定煤炭最短发火期技术,建立简便实效的数学模型,并与使用 TGA/SDTA851e同步热分析仪所得的数据进行拟合,对煤的实验最短发火期进行测算,大幅提高最短发火期预测的效率和精度,对我国研究煤自燃预测预报和煤炭自燃预防具有重要的参考价值。

固相能量守恒定律;最短发火期;数学模型

淮南煤田含煤 40层,总厚度 30～40m,其中可采煤层为 11～19层,可采厚度 23～36m。由于淮南矿区开采深度大,瓦斯涌出量高,矿山压力显现明显,巷道支护困难,褶曲、断层等地质构造发育,加之主采的 13-1煤层属高瓦斯易自燃煤层,造成淮南矿业集团现有矿井均出现过火灾现象。[1-3]发生火灾的原因主要有以下几个方面:

(1)虽然近年来对 13-1煤层自燃原因进行了研究,但其真正的自燃机理仍不甚清楚,对火灾防治措施具有一定盲目性,防灭火效果不太理想。

(2)煤自燃过程是一个相对缓慢的过程,可采取有关手段对其进行预测预报。但目前在淮南矿区火灾预测预报复杂,预测预报准确性、可靠性有待提高。

针对 13-1煤层的自燃特点,建立简便有效的预测最短发火期的方法,对研究煤自燃预测预报技术及提高 13-1煤自燃预测预报的准确率,对煤炭自燃及时预防具有重要意义。

1 煤的实验最短发火期数学模型的建立

煤在氧化过程中遵从能量守恒定律和质量守恒定律,[4-5]由此 2定律则可建立氧化过程的数学模型如下:

固相能量守恒定律:

气相能量守恒定律:

氧气质量守恒:

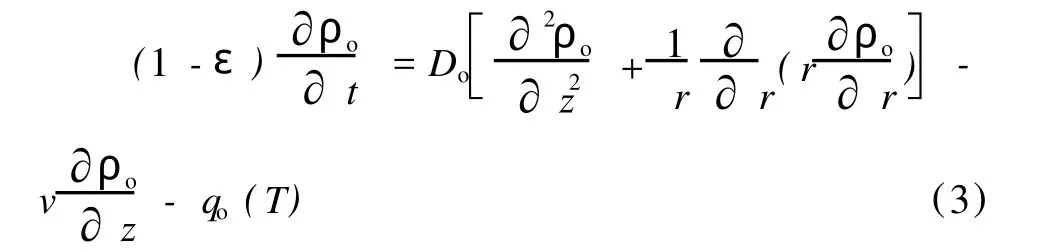
湿气质量守恒:

煤的自热氧化过程是极其复杂的,受多种因素相互影响,加上复杂的边界条件,这使得用数学方法描述这样一种物理化学现象极为困难,由于是求算煤的实验最短发火期,只要模拟出某点煤炭着火就可认为整个实验煤样都着火,本实验设定煤温达200℃时就可认为煤已自燃,将建立的模型进行相关简化:

(1)由于装置精密,已将温度变化的差值热量计入方程,则煤样就近似处在一个绝热的环境。

(2)煤样装填是均匀的、各向同性,可近似认为沿径向 (r方向)无速度梯度与温度梯度;同时进气温度在温度控制器作用下和煤样的温度接近,因此沿 z方向也没有温度梯度,煤与进出气流间没有对流换热,因此,气相能量守恒定律式可不考虑;可近似认为气样中氧浓度不变化,因此,氧气守恒等式在模拟过程中可不考虑;实验煤样经过干燥处理,水蒸气质量较少,故湿气守恒等式在模拟过程中可不考虑。

根据以上对模型公式的处理,煤的实验最短发火期的数学模型可以总归为:

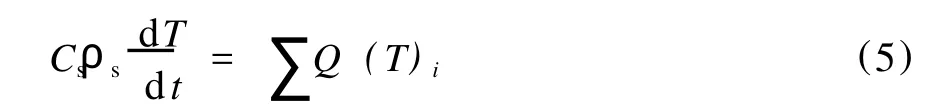
Cs为煤的比热容,J/g;ρs为煤的密度,kg/ m3;T为煤温,K;t为时间,s;Csρ是煤体温度升高消耗的热量;∑Q(T)i是煤与氧气氧化热、矿物氧化热、湿润热蒸发热等所有煤中热效应之和,可通过DSC测得。调用DSC测得结果的数据库的数据进行拟合,煤的氧化过程中的放热量∑Q(T)i与煤温 T之间关系是指数关系,结合Arrhenius公式与实测的曲线,设 ∑Q(T)i的表达式为:

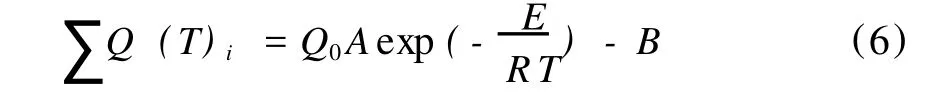
式中,Q0,B为拟合系数,A为频率因子,E为反应活化能 (kJ/mol),R为气体常数,其值为 8.31J/ (kmol)。式中系数调用 DSC测得结果的数据库的数据进行拟合。将式 (6)代入到式 (5)积分就得到煤的实验最短发火期τmin的值。

由于模拟过程中只需要 ∑Q(T)i在一定温度段 (30～200℃)的函数关系,因此,也可用多项式拟合,精度完全满足要求。在该解算程序中采用了 2～6阶的多项式对 ∑Q(T)i的函数式进行了拟合,因此,∑Q(T)i的函数关系式可写为:

式中,n为多项式的阶数,n=2～6,当求出的相关系数 R≤0.98时,解算程序中自动增加将拟合函数增加一阶;式中多项式系数调用 DSC测得结果的数据库的数据进行拟合。将式 (7)代入到式(5)中,得:

式中,T0为实验初始温度取 T0=30℃;Ti为煤的燃点温度,由于煤矿生产中煤温达 200℃时就可认为煤已自燃了,故取 Ti=200℃;τmin为煤的实验最短发火期。

2 工程应用

2.1 潘北矿 1121(3)工作面概况

该工作面位于东一采区 13-1煤层第 2块段,为一单斜构造,煤层呈块状及粉末状,煤层产状变化较大,煤层产状为:倾向 40°左右,倾角 13～42°。13-1煤厚 3.0～6.0m,平均煤厚 4.4m。本煤层瓦斯风化带平均值为 -426m,故该工作面在瓦斯风化带以下。煤层具有爆炸危险性,爆炸指数37%,具有自然发火性,自然发火期 3～6个月,本矿井恒温带深度为 30m,温度 16.8℃,地温梯度 2.3℃/100m。工作面实际温度在 26～30℃。

2.2 实验设备

煤层自燃参数测定实验设备主要有 ZRJ-1型煤自燃性测定仪、GC4085型矿井气体多点参数色谱自动分析仪、2001型煤自燃特性测试仪、TGA/ SDTA851e同步热分析仪及WS-G401型自动工业分析仪等。

2.3 煤样条件与制备

实验所取煤样为 13煤,分别取自潘北煤矿1121(3)工作面上、中、下部。

本次实验煤样的主要特点是:

(1)实验煤样多。本次实验使用的煤样为 90g左右 (平均ρs为 1.4g/cm3,平均 Cs为 39.77mJ/ kg)。

(2)原煤样是在塑料袋密封下保存,经过人工粉碎、过筛,立即放入煤样罐,基本上是属于原煤样,与采空区遗煤在物化性质方面比较接近,因此,模拟实验结果与实际情况比较符合。

(3)煤样粉碎处理。打开煤样袋将煤样粉碎、过筛和称量,然后按不同的粒度和空气流量进行实验流量和粒度的考察。

(4)实验煤样粒度范围为 0.198～0.35mm (40～80目)。

2.4 煤的实验最短发火期解算

本实验主要研究潘北矿 13-1煤在不同粒度和水分条件下吸氧量和放热量随温度的变化规律[6-10],分析 13-1煤低温氧化的规律性,并使用 TGA/SDTA851e同步热分析仪对所得的数据进行拟合,对煤的实验最短发火期进行测算,将实验室所得的结果与现场的最短发火期参照比较,以指导现场实际。

对公式 (5)中右边 ∑Q(T)i进行曲线拟合,得到拟合曲线,本次拟合采用 5阶拟合函数。拟合曲线见图1。

图1 潘北矿热量温度拟合曲线

计算方法为:

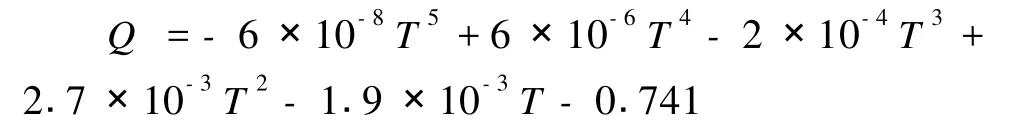
其中 R2=0.9914,对式 (5)可以改为:

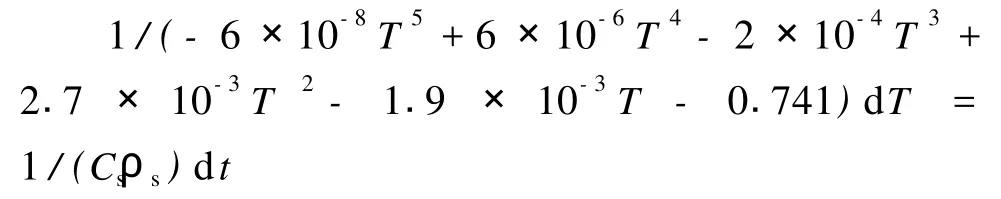
对上式左边进行积分运算,

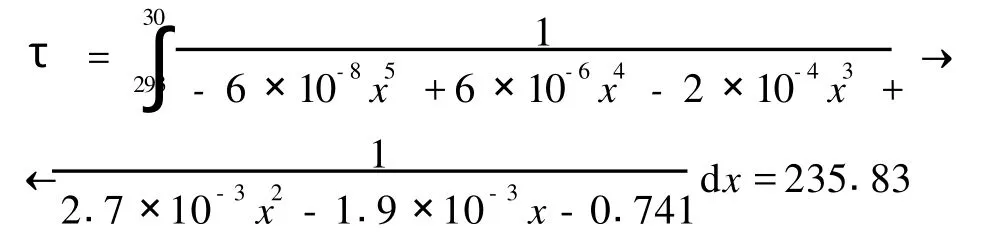
公式左边实验初始温度取 T0=30℃;终点温度为煤的燃点温度,由于煤矿生产中煤温达200℃时就可认为煤已自燃了,故取终点温度 Ti=200℃;则右边所得出的时间τmin为煤的实验最短发火期。

得出潘北矿煤样最短发火期:τmin=152d。

2.5 效果检验

本次实验测定潘北矿 1121(3)工作面煤炭自然发火期为 152d,在该工作面自然发火期 3～6个月的范围内,预测度可信,固相能量守恒定律判定煤炭最短发火期技术具有一定的可行性。

3 结束语

目前我国对煤自然发火期建立的数学模型复杂,给定参数太多,应用起来十分困难,并且和实际情况有很大的差别。固相能量守恒定律判定煤炭最短发火期技术通过提高装置精密性,煤样装填均匀性,建立简便实效的数学模型,大大提高了煤的实验最短发火期预测的效率和精度。该技术对我国研究煤自燃预测预报和煤炭自燃预防具有重要的参考意义。

[1]王省身 .矿井灾害防治理论与技术 [M].徐州:中国矿业大学出版社,1997.

[2]鲍庆国,文 虎,王秀林,等 .煤自燃理论及防治技术[M].北京:煤炭工业出版社,2002.

[3]张国枢,戴广龙.煤炭自燃理论与防治实践 [M].北京:煤炭工业出版社,2002.

[4]文 虎,徐精彩,葛岭梅,等 .煤的自燃性测试技术及数值分析 [J].北京科技大学学报,2001,23(6):499-501.

[5]邓 军,徐精彩,等 .煤最短自燃发火期实验及数值分析[J].煤炭学报,1999,24(3).

[6]吕 品 .煤炭自然发火指标气体的试验研究及其应用 [J].中国煤炭,2000(4):13-16.

[7]崔洪义,王振平,王洪权 .煤层自然发火早期预报技术与应用 [J].煤矿安全,2001(12):18-20.

[8]余明高,王清安 .煤层自然发火期预测的研究 [J].中国矿业大学学报,2001,30(4).

[9]张广文,王 旭 .煤的自燃指标气体检测 [J].矿业安全与环保,2002(5):10-11.

[10]胡社荣,蒋大成 .煤层自燃灾害研究现状与防治对策 [J].中国地质灾害与防治学报,2002,11(4):69-72.

[责任编辑:周景林]

Applying Solidoid Energy Conservation Law to Determ in ing Shortest Self-ign ition Period of Coal

ZHU Yun-hui1,CHENG Gong-lin1,FANGLiang-cai2,XIA Shi-bo2

(1.Ventilation SafetyDepartment,Huainan Vocation Technology Institute,Huainan 232001,China; 2.SafetyMining Institute,HuainanMining(Group)Co.,Ltd,Huainan 232001,China)

Utilizing solidoid energy conservation law,the paper set up a s imple and practicalmathematic model and fitwith data from TGA/SDTA851e synchronous thermal analyzer to calculate shortest self-ignition period of coal.Thismethod shortened largelyprediction efficiency and accuracy of shortest self-ignition period,which provided important reference for researching coal self-ignition period prediction and prevention.

solidoid energy conservation law;shortest self-ignition period;mathematic model

TD752.1

A

1006-6225(2010)06-0020-03

2010-07-13

国家“十一五”科技支撑计划项目“矿井深部开采安全保障技术及装备开发”HNKY-JT-JS- (2009)11号

朱云辉 (1966-),男,安徽淮南人,研究生,副教授,系主任,主要从事矿井通风与安全专业教学与研究工作。