测量平差中协因数计算教学方法之我见＊

车晓军

(武汉交通职业学院,湖北 武汉 430065)

测量平差中协因数计算教学方法之我见＊

车晓军

(武汉交通职业学院,湖北 武汉 430065)

协因数的计算是测量平差计算中的重点和难点,现有教材中的平差计算方法大多采用递推的方法,计算过程相对繁琐,不利在高职院校平差问题教学中的应用。本文从测量平差求解协因数阵的过程中,寻求采用统一变量的简便算法,以利提高高职院校平差问题教学的针对性和有效性。

应用数学;平差;高职院校课堂教学;协因数阵

0 引言

测量平差是高职工程测量技术专业的一门核心课程,着重训练该专业学生由作业层向作业管理层能力递进的重要技能。协因数是比较观测值之间相关程度的一种指标,它的计算是测量平差教学和学生学习的重点和难点,现行的教材中大多采用逐步递推的方法进行计算,变量多,关系式复杂,难以掌握,能否进行简单的直接计算而不必引用其它协因数值?本文采用将函数式统一变量进行简化改进计算。

1 协因数的现行计算方法及弊端

参照协因数传播律可以得出:

QLL=Q

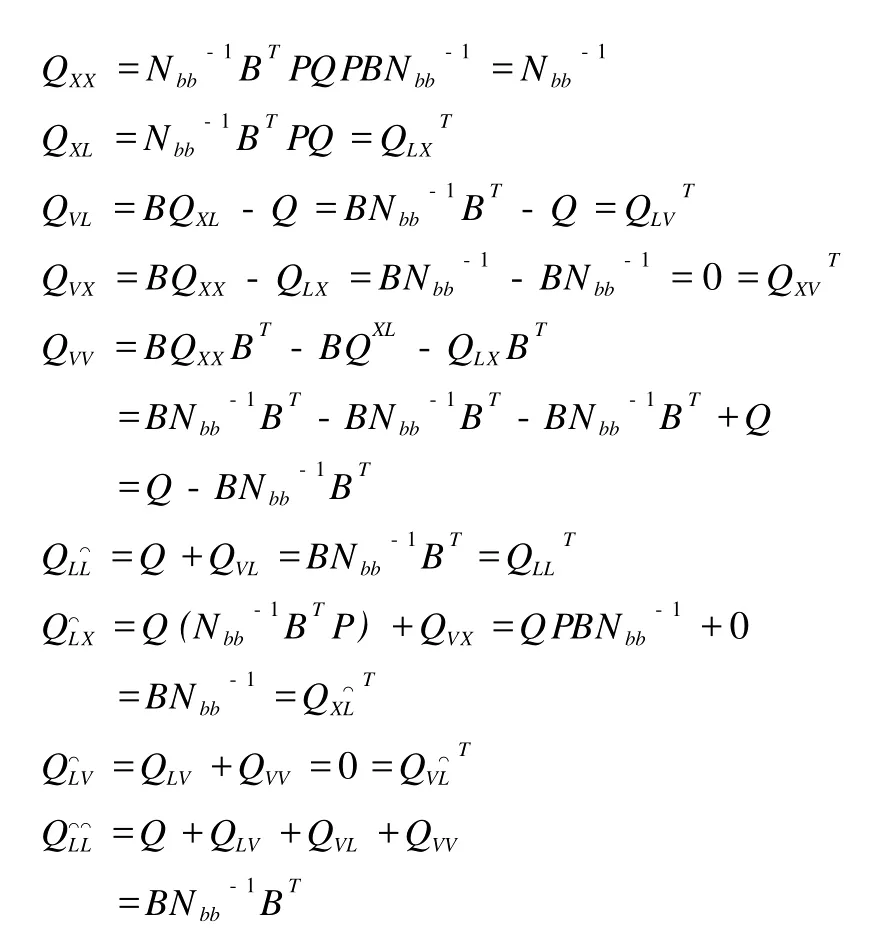
通过分析上述的协因数计算过程不难发现,其计算量较大,主要原因如下:

(1)由于采用多变量应用协因数传播律进行计算,不可避免出现连续叠代现象。

(2)计算协因数需要引用相关数据,造成计算上的不便。

2 协因数的改进计算及优势分析

2.1 改进计算方法

由于没有统一的一个变量造成了计算繁琐的情况,现采用改进措施,把自变量统一为l,按照以下算法计算:

此时将,V,全部转化为统一变量l,已知QLL=Q,根据协因数传播律,可知

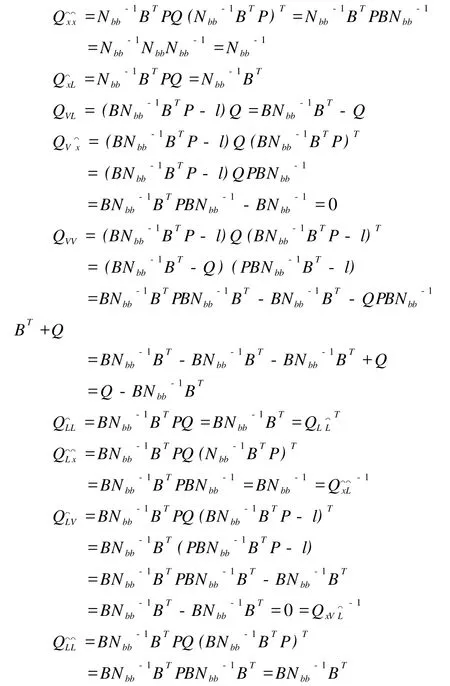
2.2 算法改进后的优势

改进计算方法后的优势有如下几点:

(1)通过统一变量计算,可以清楚明了地应用传播律进行计算,直接找到相应的统一变量函数关系式即可,不必引用原有数据,计算简练。

(2)在各种平差情况下,只要知道函数关系式即可求得相应协因数,而不需要死记硬背公式。

2.3 算例

已知:Nbb,求有关的协因数。

矩阵分析中的求逆公式为:若lAl≠0,则矩阵A可逆,且A-1其中方阵A＊为A的伴随矩阵。

在本题中,Nbb=,lNbbl=-27

3 教学效果分析

笔者在教学实践中,运用改进的计算方法进行平差问题教学,大大提高了教学的针对性和有效性,教学效果显著改进。

(1)教学课时大为减少。按照原计算方法进行教学,需要补充一定的数学知识,至少需要8-10学时,且多为理论教学;改进算法后,只需4-6学时,且可以进行2个学时的案例实训。

(2)学生应用效果好。大量的数学知识让高职学生较难理解,因而学习兴趣不浓,简便的计算方法加上一定量案例实训,不但利于学生掌握,也提高了学生解决工程测量实际问题的应用能力。

总之,通过采用改进的算法,统一变量计算,直接应用协因数传播律进行计算,方便简单,不必硬背公式,在提高计算精度的同时,方便了教学,提高了学生学习的效率,而且效果相当明显。

[1]武汉大学测绘学院测量平差学科组.误差理论与测量平差基础[M].武汉:武汉大学出版社,2003.

[2]刘丁酉.矩阵分析[M].武汉:武汉大学出版社,2003.

[3]秦晓峰,沈小成.论测量平差中的协因数计算[J].测绘通报,2010,(2).

[4]杨雪峰,龚涛,汪精河.测量平差中求解协因数的简化算法[J].测绘科学,2009,(1).

book=4,ebook=4

TP319

B

1672-9846(2010)04-0076-02

2010-07-15

车晓军(1979-),男,吉林大安人,武汉交通职业学院物流与运输系讲师,主要从事工程测量技术、桥梁结构分析与施工监控研究。