二级倒立摆系统模型建立与LQR控制仿真

万 力, 李湘敏

(1．湖南理工学院 信息与通讯工程学院, 湖南 岳阳 414006; 2．岳阳市第九中学, 湖南 岳阳 414000)

二级倒立摆系统模型建立与LQR控制仿真

万 力1, 李湘敏2

(1．湖南理工学院 信息与通讯工程学院, 湖南 岳阳 414006; 2．岳阳市第九中学, 湖南 岳阳 414000)

给出了基于牛顿力学定律的二级倒立摆结构的数学建模方法, 并应用二次型最优控制理论实现了对二级倒立摆的控制. 根据MATLAB仿真结果表明, 建模方法可行, 采用二次型最优控制对系统进行控制, 能满足控制系统稳定性、鲁棒性要求.

最优控制; 倒立摆; MATLAB仿真

Abstract:By analyzing the double inverted pendulum system, we build a mathematical model of the system which is based on Newton’s Law of mechanics and the linear quadratic optimal control strategy. The simulation on MATLAB shows that the method of the controller is feasible and the control system has good stability and robustness.

Key words:optimal control; inverted pendulum; MATLAB simulation

引言

倒立摆为典型的快速、多变量、非线性、绝对不稳定系统, 同时又是双足行走机器人和火箭垂直姿态等许多控制对象的最简模型. 由于倒立摆在数学模型上复杂但直观上又简单, 所以倒立摆机构的控制问题常用来检验控制理论及其方法的有效性, 是控制理论中较为理想的实验手段. 本文以二级倒立摆为研究对象, 利用二次型最优控制器(linear quadratic regulator, LQR)求出最优状态反馈矩阵K, 经过对Q和R两个加权矩阵的选取实现二级倒立摆的自动控制.

1 二级倒立摆模型的建立

二级倒立摆系统的机械部分主要是由小车、摆杆1、摆杆2、导轨、皮带轮、传动皮带等组成, 电气部分由电机、功率放大器、PWM、传感器、驱动电路以及保护电路组成. 其系统结构如图1所示.

先作如下假设:

(1) 摆杆1、摆杆2及小车都是刚体.

(2) 皮带轮和皮带之间无相对滑动.

(3) 小车的驱动力与支流放大器的输入成正比, 且无滞后, 忽略电极电枢绕组中的电感.

(4) 实验过程中的库伦摩擦、动摩擦等所有摩擦力足够小, 在建模过程中忽略不计.

图1 二级倒立摆结构

二级倒立摆结构参数及其设定值见表1.

表1 二级倒立摆结构参数

下面利用利用拉格朗日算子建立系统模型[1].

设Tm为小车动能, Tm1为摆杆1动能, Tm2为摆杆2动能, Tm3为质量块动能, 因此, 可以得到系统的总动能为

2 LQR控制算法

设给定系统的状态方程为X˙=AX+BU, Y=CX+DU , 用yr表示系统的期望输出, 从系统的输出端定义 e( t)=yr(t)-y( t )为系统的误差向量. 线性二次型最优算法即使得基于误差向量e构成的指标函

取最小值, 其中S, Q均为非负实数, R为r×r半正定矩阵[2].

综上所述, 具有二次型指标函数的最优控制问题, 实际上在于用不大的控制能量来实现较小的误差,以在能量和误差两个方面实现综合最优.

因为在倒立摆系统中C=I, yr( t)=0,所以Y( t)=X( t)=-e( t ), 并且倒立摆的控制是当tf→∞时线性定常系统的状态调节问题, 于是指标函数等价于

其中u=-KX为反馈控制,K=-R-1BTP , P是Raccati方程的唯一正定解.

由于在二级倒立摆系统中, 小车的位移和上下摆的摆角为主要的被控量, Q表明状态变量的影响力, R是对输入量U的加权, 经过大量反复实验和仿真, 选取R=0.2, Q=Diag(1,64,256,0,0,0),利用LQR函数得到状态反馈矩阵为

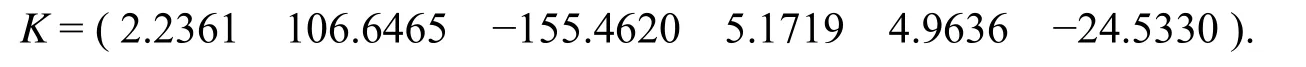
3 系统仿真

在MATLAB环境中建立二级倒立摆系统LQR控制Simulink仿真平台[3], 其结构如图2所示.

运行后得到系统的单位阶跃响应曲线如图3所示.

图2 二级倒立摆系统LQR控制Simulink仿真结构

图3 二级倒立摆系统的阶跃响应曲线

4 结论

仿真结果表明: 控制系统性能优良, 稳定性好, 具有较强的鲁棒性. 由此可见, 应用线性二次型最优控制对二级倒立摆平衡系统进行控制能够达到良好的效果, 为今后的实验研究奠定了基础.

[1] 王海英, 袁丽英, 吴 勃．控制系统的MATLAB仿真与设计[M]．北京: 高等教育出版社, 2009

[2] 郑大钟．线性系统理论[M]．第2版. 北京: 清华大学出版社, 2002

[3] 刘文斌．二级倒立摆的建模与MATLAB仿真[J]．自动化仪器与仪表, 2008(139)5: 6～7

Establishment of the Double Inverted Pendulum System Model and LQR Simulation Control

WAN Li1, LI Xiang-min2
(1. College of Information and Communications Engineering, Hunan Institute of Science and Technology, Yueyang 414006; 2. NO.9 Middle School, Yueyang 414000, China)

TP13

A

1672-5298(2010)03-0072-04

2010-06-08

万 力(1979- ), 男, 湖南岳阳人, 湖南理工学院信息与通讯工程学院讲师. 主要研究方向: 控制理论与控制算法