拉伸形变下BC3纳米管的能带结构*
2010-09-08韩文鹏刘红
韩文鹏 刘红
(南京师范大学物理系,南京210046)
(2009年6月6日收到;2010年1月18日收到修改稿)
拉伸形变下BC3纳米管的能带结构*
韩文鹏 刘红†
(南京师范大学物理系,南京210046)
(2009年6月6日收到;2010年1月18日收到修改稿)
运用紧束缚能带理论,研究拉伸形变下BC3纳米管的能带结构.研究表明:随着拉伸和压缩强度的不断增加,BC3纳米管的导带能级和价带能级逐渐靠近,最终发生能带交叠.压缩形变下能带的交叠程度可达0.5 eV,而拉伸形变下只有0.2 eV.对于扶手椅型BC3纳米管,随着拉伸和压缩的不断增加,BC3纳米管首先由直接半导体转化为间接半导体,进而发生能带的交叠,表现出金属性.在无形变时,扶手椅型BC3纳米管是一种很不稳定的直接跃迁窄带半导体,轻微的压缩形变(et=-0.003)都可以使其转化为间接半导体.对于锯齿型BC3纳米管,由于存在平坦的导带和价带,轻微的拉伸和压缩形变会使原来全波矢允许的直接跃迁变为只允许一个波矢的直接跃迁.
BC3纳米管,能隙,拉伸形变,半导体
PACC:7125X,7155,7320D
1. 引言
自从发现碳纳米管[1]以来,它的结构和特殊性质以及潜在的应用价值,使其成为纳米元器件的佼佼候选者,已经引起实验物理学家、理论物理学家、材料物理学家,还有化学家,甚至生物学家们极大的关注和研究兴趣.至今对碳纳米管的研究不仅仅局限于纯碳材料,替代式掺杂纳米管及其衍生物的性质也引起人们广泛的兴趣.研究已经发现,用B原子替代C原子的BC3纳米管是一种窄带隙半导体材料,其带隙与纳米管的直径和手性基本无关[2].因此,BC3纳米管非常适合进行量子效应的研究,在电子器件和纳米复合材料领域有很好的应用前景.近些年来,Guo等[3]采用经验力常数模型计算了扶手椅型和锯齿型BC3纳米管的声子色散关系,Chen等[4]利用梯度近似方法计算了BC3纳米管的光学吸收谱,文献[5]基于力常数模型计算了不同直径BC3纳米管拉曼活性模和红外活性振动模的频率与管径的关系.但是目前未见有关拉伸形变对BC3纳米管能带结构影响的研究报道.
本文在紧束缚理论[6]的基础上计算拉伸形变对不同BC3纳米管能带结构的影响,表明轴向拉伸和压缩均会导致BC3纳米管能带结构发生复杂的变化,出现直接跃迁半导体到间接跃迁半导体的转变,继而出现导带与价带的交叠,发生半导体性到金属性的转变.
2. 拉伸形变下BC3纳米管的能带结构
如图1所示,BC3纳米管的原胞内包含8个原子,其中2个B原子和6个C原子,即B和C的比例是1∶3.不同类型的BC3纳米管的结构参数表达式与碳纳米管完全相同,仍可采用一对整数(n,m)表示,即BC3纳米管(n,m)是由单层BC3平面以矢量R=na1+ma2为圆周方向,首尾相重合卷曲而成,纳米管半径为
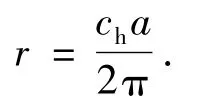
这里为单层BC3平面基矢,,其中b1=0.155nm为B—C键键长,b2=0.142nm为C—C键键长[7].与碳纳米管确定方法相同,BC3纳米管沿管轴方向的周期长度

其中gcd(2n+m,n+2m)表示求(2n+m)和(n+ 2m)的最大公约数.在一个周期内的原胞数Nh=2c2h/gcd(2n+m,n+2m),原子数为8Nh,电子数为6Nh.
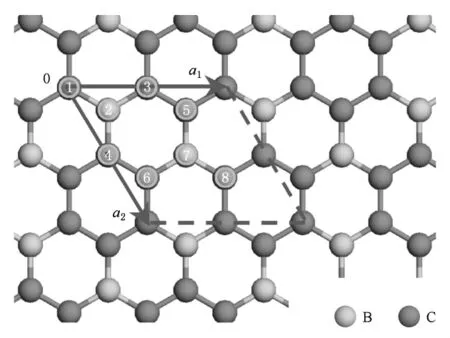
图1 BC3纳米管结构示意图
在紧束缚近似下[6],哈密顿量可表示为
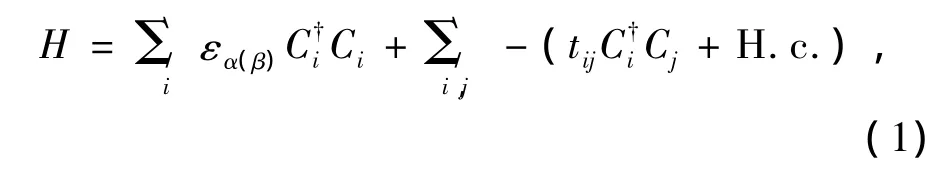
其中C†i(Cj)表示在第i(j)个原子上电子的产生(湮没)算符;εα(β)为格点占位能,对于C原子,εC=-8.1 eV,对于B原子,εB=-7.0 eV[7];tij表示最近邻格点之间的跃迁系数.因有B和C两种原子,故有B—C键和C—C键两种.无形变时跃迁系数对于不同的键分别取为[7]tCC=-2.2 eV,tBC=-2.4 eV.当发生形变时,最近邻原子i和j之间的键长为rij,跃迁系数与键长的关系采用Harrison近似[8],tij=t0(r0/rij)2,其中r0为无形变时B—C键键长b1或C—C键键长b2,t0是没有形变情况下最近邻原子i和j之间的跃迁系数.无形变时,BC3纳米管是一种窄带隙半导体材料,禁带宽度为0.31 eV,而且带隙不随纳米管的直径和手性变化,与文献[2]报道一致.
对于拉伸形变,用et表示轴向拉伸参数.因拉伸引起的径向变化用泊松比描述,与碳纳米管相同[9],本文中泊松比取为ec=-0.2et.对于原胞中的8个原子有6种不同的键矢量δi,如图1所示.在拉伸形变下,键矢量随拉伸参数的变化关系
如下:
因此,6种不同的最近邻原子之间的跃迁系数随拉伸参数的变化关系为
因为C原子和B原子格点能不同,且由于B原子缺少一个π电子,故填充电子的最高能带并不位于所允许能量范围的中心处.这些导致BC3纳米管能带结构不具有电子与空穴的对称性.进一步,由于掺杂导致对称性降低、原胞扩大、能带的简并度较低,因此BC3纳米管的能带结构远比纯碳纳米管复杂.
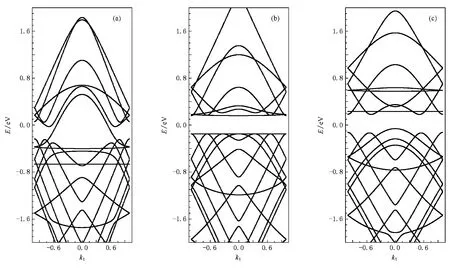
图2显示了扶手椅型BC3纳米管(3,3)时的能带结构.无形变时,在能带结构(图2(b))中,费米能EF=0 eV附近有多个极值点,Γ点和kt=±0.67.虽然扶手椅型BC3纳米管导带底和价带顶都在Γ点,是直接跃迁半导体,但在kt=±0.67极值点,导带和价带的能级差与Γ点禁带宽度相差很小.这个极值特征将导致在轴向压缩和拉伸形变下BC3纳米管的能带结构变化要比纯碳管复杂.如图2(a),(c)所示,BC3纳米管在形变量et=-0.1,0.1时,不仅能隙为零,而且能带出现交叠现象.而纯碳纳米管在拉伸和压缩形变下,导带底和价带顶的波矢位置不随形变改变,没有出现能带交叠现象[10].
当拉伸BC3纳米管(3,3)时(图2(a)),Γ点导带向费米能靠近,kt=±0.67处导带则远离费米能向上移动,而价带整体稍稍向上,向费米面移动.当et=0.1时,极值点kt=±0.525处的价带顶移动变化较大并越过费米能,与Γ点的导带形成交叠.但是在BC3纳米管(3,3)压缩形变时(图2(c)),Γ点导带稍稍向上远离费米能,kt=±0.48处导带向下大幅度移动并越过费米能,Γ点价带大幅度升高,而极值点处kt=±0.67的价带向下大幅度移动,最终极值点kt=±0.67处的价带和Γ点导带形成交叠.
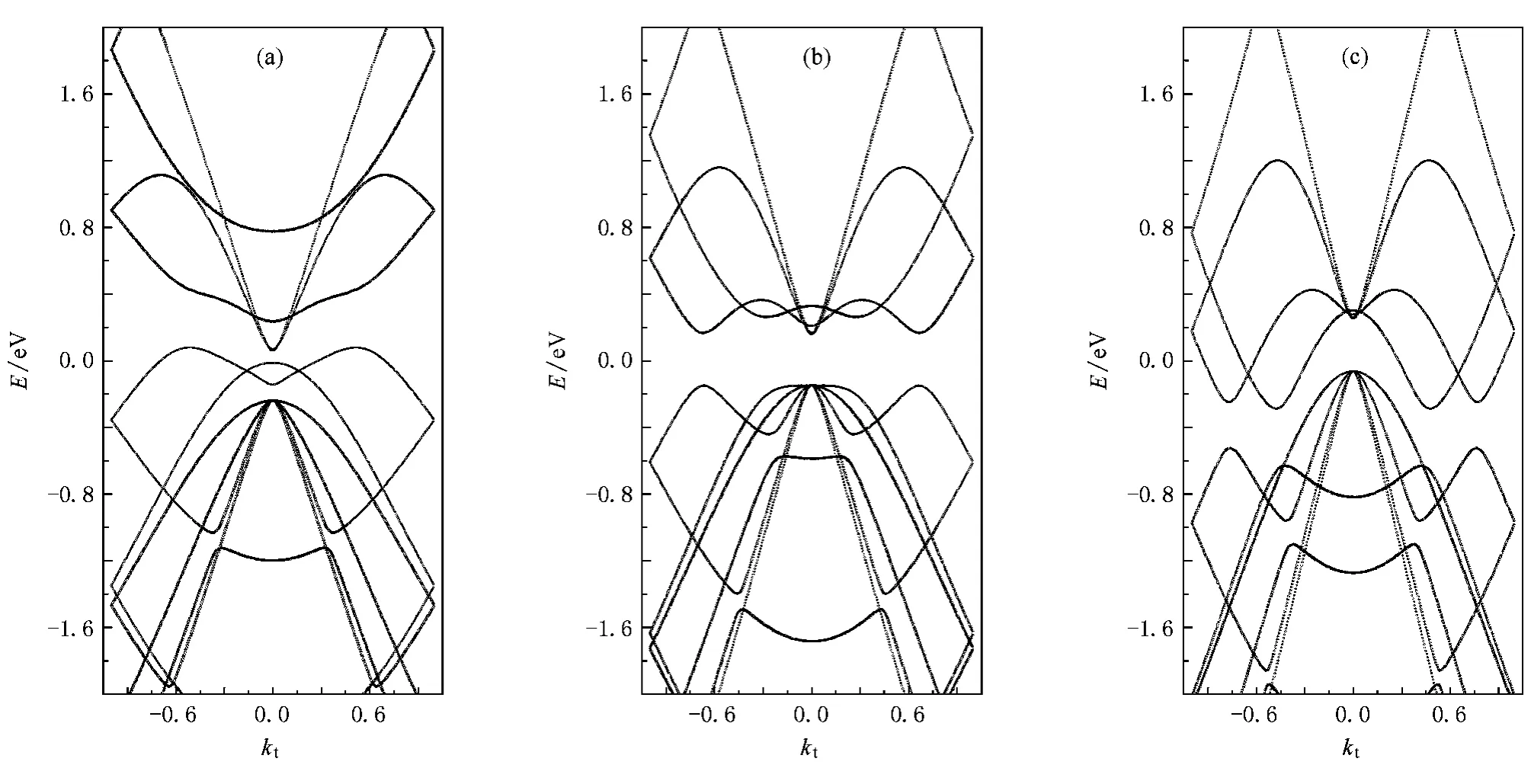
图2 形变对BC3纳米管(3,3)能带结构的影响(a)et=0.1,(b)et=0.0,(c)et=-0.1
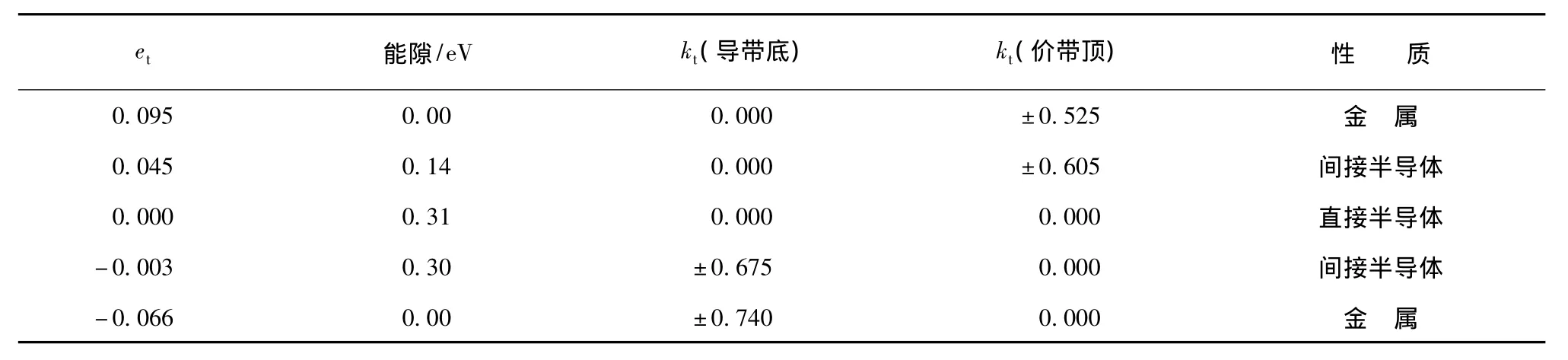
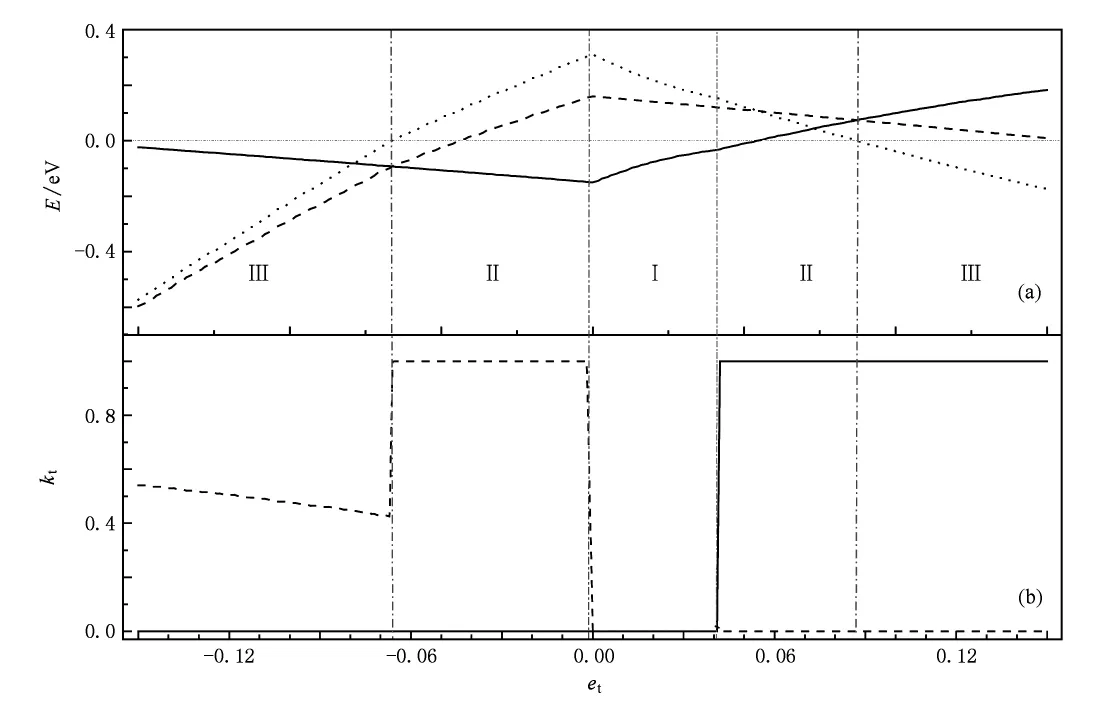
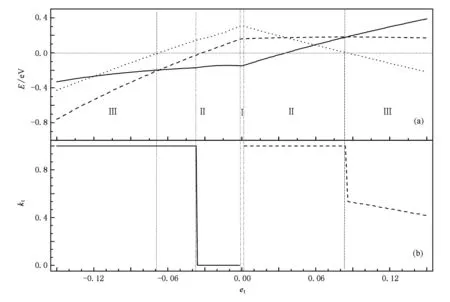
图3(b)和表1给出了导带底和价带顶的能量和波矢位置随形变参数的变化关系.在拉伸形变过程中,当0 图3 BC3纳米管(3,3)禁带宽度、导带底和价带顶的能量和位置随形变的变化关系短划线表示导带底,实线表示价带顶,点线表示禁带宽度.Ⅰ区为直接跃迁半导体性区域,Ⅱ区为间接跃迁半导体性区域,Ⅲ区为金属性区域.(a)禁带宽度、导带底和价带顶的能量随拉伸参数的变化,(b)导带底和价带顶的波矢位置kt随拉伸参数的变化 表1 BC3纳米管(3,3)能带结构及性质随参数的变化 对于不同n值的扶手椅型BC3纳米管,计算结果表明,当n为偶数时,与导带底能量和价带顶能量对应的能带指标l和kt随拉伸形变发生跃变的转变点基本与n为奇数时一致,如图4所示.BC3纳米管(4,4)在拉伸形变过程中,当0 从图3和图4还可以看出,无形变时,扶手椅型BC3纳米管是一种不稳定的直接跃迁窄带半导体.轻微的压缩形变(et=-0.003)都可以让它转化为间接半导体.扶手椅型BC3纳米管在拉伸情况下容易保持窄带直接跃迁半导体性质,只有当拉伸达到一定程度时(et=0.042附近)才转变为间接半导体. 拉伸和压缩形变的(6,0)锯齿型纳米管的能带结构见图5所示.无形变时,最低导带和最高价带都是平坦的能带(图5(b)),可形成能量稳定的各种波矢允许的直接跃迁.然而发生形变时,虽然这两个平坦能带的形状及两带之间的能量间距不随形变发生改变,但是这两个带的能量位置会随形变量的增加而发生移动,并且其他价带和导带变化剧烈.因此,拉伸形变下锯齿型BC3纳米管能带结构的变化与扶手椅型BC3纳米管差别很大. 图4 BC3纳米管(4,4)禁带宽度、导带底和价带顶的能量和位置随形变的变化关系短划线表示导带底,实线表示价带顶,点线表示禁带宽度.Ⅰ区为直接跃迁半导体性区域,Ⅱ区为间接跃迁半导体性区域,Ⅲ区为金属性区域.(a)禁带宽度、导带底和价带顶的能量随拉伸参数的变化,(b)导带底和价带顶的波矢位置kt随拉伸参数的变化 如图5(a)和图6(a),(b)所示,在压缩形变下,随着压缩程度的增加,两个平坦的能带都逐渐下移,当et=-0.002时,原价带在kt=0处的能量低于其他kt的价带,而价带顶对应的波矢位置变为kt=0,此时能隙尚不为零.当et=-0.036时,kt=0处价带低于kt=±1处的价带,价带顶对应的波矢位置变为kt=±1,此时能隙尚不为零.形变量继续增加,在位置保持不变的情况下,当et=-0.066时,导带底能量和价带顶能量(kt=±1)重合,带隙消失,BC3纳米管由半导体性转化为金属性.当et<-0.066时,导带能量和价带能量发生交叠.如图5(c)和图6(a),(b)所示,在拉伸形变下,两个平坦能带的形状不随拉伸改变,只是随拉伸量的增加,能量位置升高.当et>0.002时,原最低导带能量高于kt=±1处的其他导带,导带底对应的波矢位置变为kt=±1,此时能隙尚不为零.随着拉伸程度的增加,在et<0.085时,导带底仍在此位置保持不变.当et=0.085时,导带底能量和价带顶能量(kt=±1)重合,带隙消失,BC3纳米管由半导体性转化金属性,同时导带底对应的波矢位置发生突变,由kt=±1变为kt=±0.535,并随着拉伸程度的增加逐渐向Γ点靠近. 分析图3(a)、图4(a)、图6(a)和图7可以发现,不同螺旋度的BC3纳米管均随着拉伸或压缩程度的不断增强,导带底能量都会逐渐降低,同时价带顶能量逐渐升高,导致最后导带能级和价带能级发生交叠,BC3纳米管逐渐由半导体性转化为金属性.同时,我们比较拉伸和压缩形变引起的能带变化发现,压缩形变下纳米管的导带能级变化较大,拉伸形变下价带能级变化较大.压缩形变下价带能级和导带能级的交叠明显强于拉伸形变对纳米管的影响,在形变强度均为0.15时,压缩形变下能级交叠可达0.5 eV,而拉伸形变下只有0.2 eV左右. 图5 形变对BC3纳米管(6,0)能带结构的影响(a)et=-0.1,(b)et=0.0,(c)et=0.1 图6 BC3纳米管(6,0)禁带宽度、导带底和价带顶的能量和位置随形变的变化关系短划线表示导带底,实线表示价带顶,点线表示禁带宽度.Ⅰ区为直接跃迁半导体性区域,Ⅱ区为间接跃迁半导体性区域,Ⅲ区为金属性区域.(a)禁带宽度、导带底和价带顶的能量随拉伸参数的变化,(b)导带底和价带顶的波矢位置kt随拉伸参数的变化 图7 不同螺旋度的BC3纳米管的禁带宽度、导带底和价带顶的能量随拉伸参数的变化短划线表示导带底能量,实线表示价带顶能量,点线表示带隙.(a)(5,1),(b)(5,2),(c)(5,3) 本文运用紧束缚方法计算BC3纳米管在拉伸形变和压缩形变下的能带结构.计算结果表明,随着拉伸度和压缩程度的增加,扶手椅型、锯齿型和不同螺旋度的BC3纳米管的能隙将减小,最后都会发生导带与价带的交叠,导电性由半导体性转化为金属性.并且压缩形变下价带能级和导带能级的交叠程度明显强于拉伸形变对纳米管的影响.对于不同螺旋度的BC3纳米管,因导带和价带的不同,能带的变化和交叠的方式不相同.对于扶手椅型BC3纳米管,轻微的轴向形变都会导致价带顶和导带底对应的波矢位置不相同,使得BC3纳米管由直接半导体转化为间接半导体.随着拉伸和压缩程度的不断增加,能带进而发生交叠,表现出金属性质.扶手椅型BC3纳米管在无形变时是一种很不稳定的窄带半导体.而对于锯齿型BC3纳米管,费米面附近的两个平坦能带的能量位置将随形变做整体平移.但是轻微的拉伸和压缩形变会使价带顶和导带底的位置发生突变,使得原来全波矢允许的直接跃迁变为只允许一个波矢的直接跃迁. [1]Iijima S 1991 Nature 354 56 [2]Miyamoto Y,Rubio A,Louie S G,Cohen M L 1994 Phys.Rev. B 50 18360 [3]Guo Z X,Xiao Y,Ding J W,Yan Y H 2006 Phys.Rev.B 73 045405 [4]Chen S C,Chen I Y,Ho Y H,Lin M F 2006 J.Vac.Sci. Technol.B 24 46 [5]Wang H,Feng M,Cao X W,Wang Y F,Jin Q H,Ding D T,Lan G X 2008 Acta Phys.Sin.57 5143(in Chinese)[王翚、冯敏、曹学伟、王玉芳、金庆华、丁大同、蓝国祥2008物理学报57 5143] [6]Huang K,Han R Q 2005 Solid State Physics(Beijing:Higher Education Press)(in Chinese)[黄昆、韩汝琦2005固体物理(北京:高等教育出版社)] [7]Wentzcovitch R M,Cohen M L,Louie S G,Tománek D 1988 Solid State Commun.67 515 [8]Harrison W A 1999 Elementary Electronic Structure(Singapore: World Scientific Publishing)p262 [9]Yang L,Han J 2000 Phys.Rev.Lett.85 154 [10]Liu H,Yin H J,Xia S N 2009 Acta Phys.Sin.58 8089(in Chinese)[刘红、印海建、夏树宁2009物理学报58 8089] PACC:7125X,7155,7320D *Project supported by the National Natural Science Foundation of China(Grant No.10947004),the Natural Science Foundation of Jiangsu Province,China(Grant No.BK2008427)and the Doctoral Program Foundation of Institution of Higher Education,China(Grant No. 200803190004). †Corresponding author.E-mail:liuhong3@njnu.edu.cn Band structures of strain-deformed BC3nanotubes* Han Wen-Peng Liu Hong† By using the tight-binding energy band theory,we study the band structures of BC3nanotubes under stretching and compressing deformations,the conductivity band turns more and more close to the valence band of the BC3nanotubes and eventually they overlap each other with the increase of tension.Furthermore,the results obtained show that the overlap under compressing is bigger than that under stretching.The biggest overlap under compressing is up to 0.5 eV,but it is only 0.2 eV under stretching.In addition,for armchair BC3nanotubes,the results of band structures show that with the increase of tension,the BC3nanotube transforms into an indirect semiconductor from a direct semiconductor,and then leads to the band overlap.The armchair BC3nanotube is an unstable narrow-gap semiconductor,because a little compress (et=-0.003)can convert it transform into an indirect semiconductor from a direct semiconductor.For zigzag BC3nanotubes,a slight deformation can turn into a direct semiconductor having only one allowed wave vector from a direct semiconductor having all wave vectors,owing to the existence of two flat conductivity and valence bands. BC3nanotube,energy gap,strain-deformation,semiconductor book=268,ebook=268 *国家自然科学基金(批准号:10947004)、江苏省自然科学基金(批准号:BK2008427)和高等学校博士学科点专项科研基金(批准号: 200803190004)资助的课题. †通讯联系人.E-mail:liuhong3@njnu.edu.cn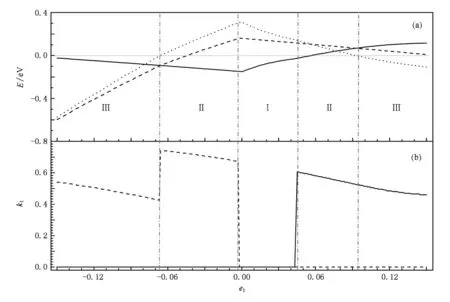

3. 结论
(Department of Physics,Nanjing Normal University,Nanjing210046,China)
(Received 6 June 2009;revised manuscript received 18 January 2010)
