一种两步自适应抗差K alman滤波在GPS/INS组合导航中的应用

吴富梅,杨元喜

1.信息工程大学测绘学院,河南郑州450052;2.西安测绘研究所,陕西西安710054

一种两步自适应抗差K alman滤波在GPS/INS组合导航中的应用

吴富梅1,2,杨元喜2

1.信息工程大学测绘学院,河南郑州450052;2.西安测绘研究所,陕西西安710054

针对伪距、伪距率紧组合导航精度低、姿态角误差修正误差较大的缺点,从参数可观测性角度提出一种两步自适应Kalman滤波算法。首先简单介绍紧组合Kalman滤波的过程,然后给出两步自适应抗差滤波的公式和具体步骤,并且进行分析和比较。最后用实测算例对提出的算法进行验证。结果表明,相比于伪距、伪距率紧组合Kalman滤波,两步自适应抗差滤波的导航精度受组合周期的长短、INS惯性元件误差的大小影响较小,精度略有提高,更重要的是能够控制动态扰动异常和观测异常的影响,在惯性元件误差较大的情形下也能够很好地估计元件误差,避免姿态角错误修正。

分步自适应Kalman滤波;GPS/INS组合导航;紧组合导航;自适应因子

1 引 言

全球定位系统(GPS)和惯性导航系统(INS)具有很强的功能互补性,将两者组合起来可以有效地利用各自的优点,进行系统间的取长补短以减小系统误差影响,提高导航系统的性能,目前已在陆海空导航领域受到广泛的应用。GPS/INS组合导航系统不仅能够提供载体的位置、速度和姿态信息,而且能够实现长时间导航定位的高精度,高数据采样率以及抗差性[1-2]。

在GPS/INS组合导航中,紧组合方式因为观测量不相关,而且在卫星少于4颗的情况下,也能在较短的时间里实现 GPS/INS数据融合,因而备受关注[1]。紧组合中对速度进行校正一般采用多普勒观测值,对位置进行校正可以采用伪距或采用载波相位作为观测量。采用伪距可避免求解模糊度和处理周跳等问题,但是由于伪距的观测噪声较大、残留误差大,实时导航的精度较低,不能精确校正INS的误差;采用载波相位作为观测量,导航精度高,但是需要解算模糊度,实时导航时过程复杂、模糊度解算可靠性较低,很难满足连续、可靠、高精度的导航要求[3]。另外,用载波相位进行实时导航需要利用参考站进行差分解算,从而增加了成本,而且导航精度还受到用户与基准站距离的限制[4]。

将GPS/INS数据通过一定的算法融合形成最优解是组合导航的关键。目前 Kalman滤波是最普遍采用的一种方法[5]。为了克服 Kalman滤波次优甚至发散的缺点,在载体动态导航中,一般利用自适应滤波来控制动态扰动异常、动态模型误差以及随机误差的影响[6-7]。在GPS/INS组合导航Kalman滤波解算模型中观测往往个数小于状态参数个数,只能利用预报残差来构造自适应因子,这就需要观测量可靠、观测精度较高[8]。而且,在利用Kalman滤波对INS误差进行估计时不仅需要可靠的随机模型还需要高精度的观测量[9],显然,伪距观测量一般不能满足要求。另外,伪距易受到外界影响,观测中难免存在粗差。

基于此,本文提出一种两步自适应抗差 Kalman滤波算法。首先考虑利用高精度的多普勒观测值进行一步自适应 Kalman滤波对组合导航系统误差进行校正,然后用校正后的动态系统模型信息与低精度的伪距观测量进行二步抗差Kalman滤波。

2 GPS/INS紧组合 K alman滤波

在GPS/INS紧组合导航中,系统的状态由两部分组成:一是INS的误差状态;二是 GPS的误差状态,观测量由INS导航结果推算的伪距、伪距率与 GPS观测得到的伪距、伪距率作差得到[10-11]。

系统的状态方程为

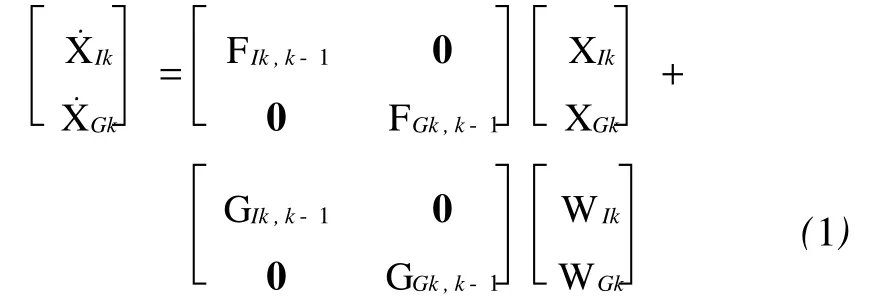
系统的观测方程为

式中,FIk,k-1为 INS连续系统的状态转移矩阵; GIk为INS系统的动态噪声矩阵;WIk为INS系统的过程白噪声矢量;FGk,k-1为 GPS连续系统的状态转移矩阵;GGk为 GPS系统的动态噪声矩阵; WGk为 GPS系统的过程白噪声矢量;XIk为15维未知参数向量,表达式为 XIk=[δx δy δz δ˙x δ˙y δ˙z φxφyφzεxεyεzaxayaz]T;XGk为二维未知参数向量,表达式为 XGk= [CδtuCδtru]T;C为光速;Lρk和˙L˙ρk为观测向量; Aρ1、Aρ2、A˙ρ1和A˙ρ2为观测矩阵中的分块矩阵;n为可测卫星的个数,表达式具体意义和定义见文献[10]。

在这里,为了便于下面的分析,将状态参数的顺序重新调整分为直接可测参数 X1和间接可测参数 X2两个部分。在伪距、伪距率紧组合Kalman滤波中,X1和 X2分别为

相应的状态矩阵、观测矩阵以及噪声矩阵也按照估计参数的顺序作相应调整,则连续系统状态方程为

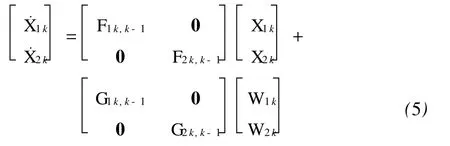
观测方程为

式中,

对式(5)离散化,联列状态方程和观测方程进行 Kalman滤波,则导航解为[5,12]

式中,Kk称为Kalman滤波增益矩阵

式中,Ak为观测矩阵;Φk,k-1为状态转移矩阵。

令

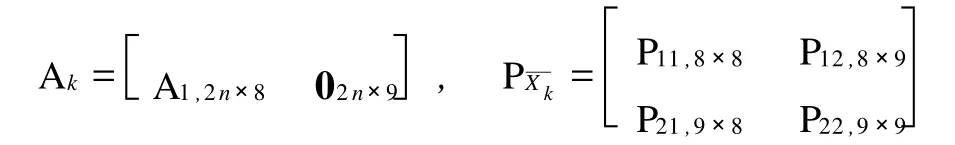
则式(7)可写成[9]

由式(8)可得

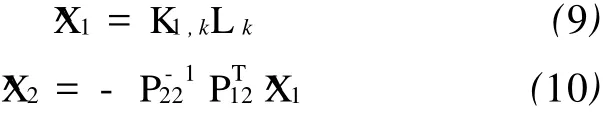
若观测协方差阵和状态协方差阵可靠,间接可测参数X2的估计依赖于直接可测参数 X1的估计,若 X1的估计精度较低,就会影响 X2的估计精度。在 GPS/INS伪距、伪距率紧组合系统中,因为伪距的观测噪声较大,造成可测参数 X1中的位置误差参数的估计精度较低,由此得到的间接可测参数 X2的精度也会降低,用此估计值对INS误差进行校正,必然会影响INS误差的校正结果。

3 两步自适应 K alman滤波算法

在 GPS/INS伪距、伪距率紧组合系统中, Doppler观测值具有较高的观测精度,计算的速度具有厘米级精度,可以用来对滤波间接可测参数进行估计。设计的方案是采用两步 Kalman滤波。在第一步 Kalman滤波中,利用高精度的速度参数对INS误差估计并进行修正;为避免误差累积,第二步Kalman滤波中,利用伪距观测量对INS一步修正后的位置误差再进行修正。

3.1 基于Doppler观测值的一步自适应 K alman滤波

在第一步 Kalman滤波中,观测量仅用Dopplor观测值,因此直接可测参数 X1和间接可测参数X2为

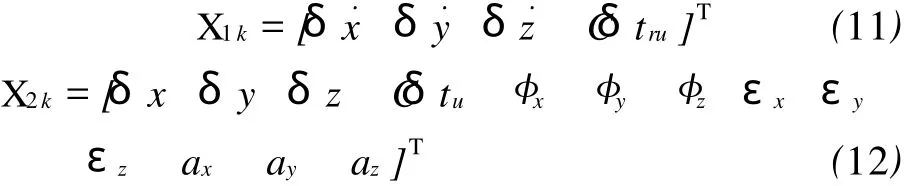
状态方程参照式(1)按照参数的顺序作相应调整,这里状态方程中的元素并未变化,只是位置发生变化。

观测方程为

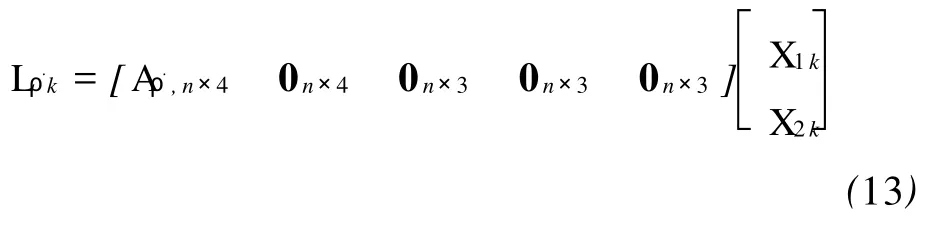
为控制扰动异常的影响,引入自适应滤波[5-7]。自适应滤波解为

式中,αk为自适应因子。

因为观测个数小于状态参数的个数,基于预报残差¯Vk构造统计量为[8]

自适应因子αk为

式中,c为常量,可以取c=0.85～1.0。

因为直接可测参数 X1的估计精度较高,可以用间接可测参数的滤波估计值对INS系统误差进行校正。

一般地,在伪距、伪距率紧组合中是利用上面的Kalman滤波得到的误差改正量直接对INS推算得到的位置和速度进行修正,即

但是,在基于Doppler观测值的一步自适应Kalman滤波中,由观测方程式(13)可知,只有速度是直接可测参数,其他都是间接可测参数。用这样的结果对位置进行修正,必然还会存在一定的偏差。考虑在短时间内速度变化较小,可以用经过正确修正的速度,重新对位置进行推算,即

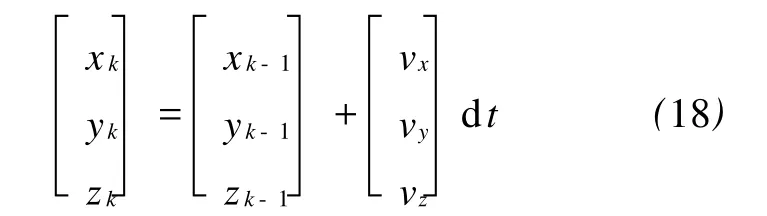
式中,dt为修正的时间间隔。

3.2 基于伪距观测值的二步抗差 K alman滤波

在第二步 Kalman滤波中,为避免推算的误差累积,再采用伪距观测值进行 Kalman滤波,因此直接可测参数X1和间接可测参数X2为

与式(12)中的状态方程类似,其元素按照参数的顺序作相应调整。

观测方程为

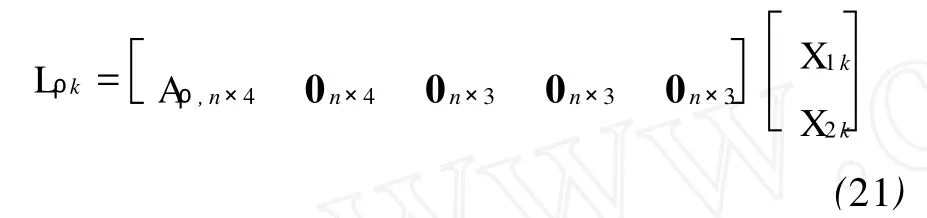
这里因为观测量精度较低,而由速度推算的位置短时间内精度较高,以推算速度作为参考,为抵制伪距观测粗差的影响,利用抗差等价权来控制观测异常的影响[15]。等价权函数为[16]

式中,Δ˜vk,i为第 i个伪距观测量的标准化预测残差。

需要指出的是,上面是为了方便分析将状态参数调整顺序,在实际计算过程中,参数的顺序无需调整。

通过对紧组合Kalman滤波与两步自适应抗差Kalman滤波比较,可知:

1.在紧组合 Kalman滤波中采用的是 INS推算的位置和速度与 GPS观测量进行滤波。在两步自适应抗差 Kalman滤波的一步滤波中,采用的是INS推算的速度与 GPS Doppler值进行滤波,而在二步滤波中,采用的是经过一步滤波修正后的位置与 GPS伪距进行滤波。这对于精度较高或者组合周期较短的组合导航系统其差别不明显,但是对于精度较低、组合周期较长的组合导航系统其改善效果明显,因为INS的精度越低、单独导航时间越长累积的误差就越大。

2.在紧组合 Kalman滤波中,直接可测参数是位置和速度,由于位置的估计精度较低,将直接影响间接可测参数姿态角误差、陀螺仪和加速度计误差的估计;在分步自适应 Kalman滤波中,直接可测参数是精度较高的速度参数,因此提高了间接可测参数姿态角误差、陀螺仪和加速度计误差的估计精度。

3.在分步自适应 Kalman滤波中,通过一步自适应因子的调节可以控制状态模型误差的影响,通过二步等价权函数抵制观测粗差的影响。

4 计算与分析

取一组 GPS/INS车载导航数据进行试验。INS配备战术级惯性元件,测量精度较高,采样频率为100 Hz,GPS数据采样频率10 Hz。算例中,下列参数由经验确定:陀螺仪和加速度计误差相关时间分别为600 s,600 s;陀螺仪和加速度计初始均方差分别取10.0 deg/h和100μg;初始位置误差为5 m,5 m,7 m;初始速度误差为0.1 m/s;初始平台失准角误差分别为100.0 s,100.0 s和500.0 s;采用GPS伪距和多普勒观测值进行紧组合导航解算时,初始方差取25 m2和0.01 m2/s2。图1给出了行车轨迹。

图1 行车轨迹Fig.1 Tracking figure

采用两种方案进行组合导航:

方案1:伪距、伪距率紧组合Kalman滤波;

方案2:分步自适应Kalman滤波。

为了验证分步自适应 Kalman滤波的性能,对上述数据进行处理,分为四种情形:

1.原始数据,组合周期0.1 s;

2.为验证自适应滤波的效果,在轨迹图中标注处6个历元(每个标注两个比较接近的历元), GPS 2,10号卫星伪距观测值中加入30 m,20 m粗差,在载体速度预测向量中随机加入10 m,5 m扰动,组合周期0.1 s;

3.为验证组合周期对两种滤波算法的影响,采用原始数据导航,组合周期1.0 s;

4.为验证INS观测精度对两种算法的影响,在INS原始数据中加入白噪声误差,陀螺仪误差为(0,0.1°/s),加速度计误差为(0,0.000 01 m/s2),组合周期为1.0 s。

两种算法在四种情形下导航误差见图2～图5,由于 X,Y,Z方向的误差相似,在此只给出X方向的误差图。图6和图7给出了情形4下两种方案航向角与参考值的比较。表1给出了两种算法在四种情形下导航误差的RMS比较。

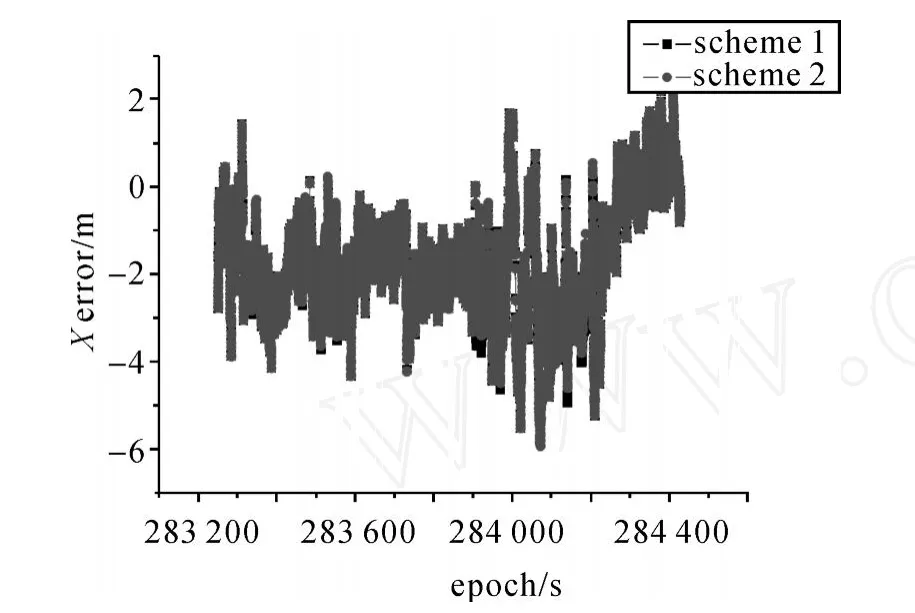
图2 情形1X方向误差Fig.2 Xerrors of case 1

图3 情形2X方向误差Fig.3 Xerrors of case 2

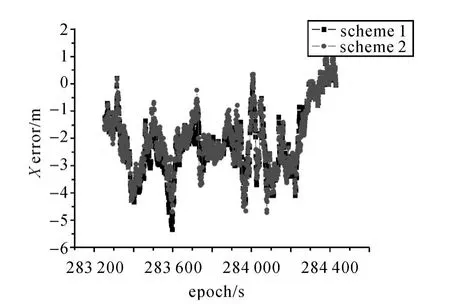
图4 情形3X方向误差Fig.4 Xerrors of case 3

图5 情形4X方向误差Fig.5 Xerrors of case 4

图6 情形4方案1航向角与参考值比较Fig.6 Comparison of yaw angle with reference by Scheme 1 of case 4

图7 情形4方案2航向角与参考值比较Fig.7 Comparison of yaw angle with reference by scheme 2 of case 4

分析上面的结果,可以得出:

1.在组合周期较短、INS惯性元件误差较小的情形下,伪距、伪距率紧组合 Kalman滤波与两步自适应抗差 Kalman滤波的导航精度相当。

2.从情形2的算例可以看出,当状态向量存在扰动时,两步自适应抗差 Kalman滤波通过一步自适应因子控制了扰动异常的影响;当伪距观测中存在观测粗差时,通过二步滤波中的等价权函数抵制了观测异常的影响,相比于紧组合Kalman滤波,提高了系统抵制状态异常和粗差的能力。

表1 四种情形下两种方案的Mean Error比较Tab.1 Mean Error by two schemes of four cases

3.在组合周期较长或者惯性元件误差较大的情形下,两步自适应抗差 Kalman滤波的导航精度要优于紧组合 Kalman滤波,这是因为分步自适应滤波采用的是经过一步滤波修正后的位置与GPS伪距进行滤波的结果;对比情形3和情形4还可以看出,惯性元件误差对紧组合Kalman滤波的影响更大,组合周期的影响稍小。

4.当惯性元件误差较大时,在紧组合Kalman滤波中,由于伪距观测误差较大,造成间接可测参数估计误差较大,惯性元件误差被错误修正,因此航向角误差较大;在两步自适应抗差Kalman滤波中,由于采用高精度的Doppler观测值作为观测量,提高了间接可测参数估计精度,误差得到很好的修正,航向角保持较高的精度。俯仰角和横滚角也具有相同的情形。需要说明的是,间接可测参数得到很好估计不仅需要较高精度的直接可测参数,还需要可靠的误差随机模型,两者缺一不可。

5 结 论

综上所述,在采用伪距、伪距率紧组合 Kalman滤波时,由于直接采用INS推算的位置和速度与GPS观测组合,导航精度随着组合周期的增长、惯性元件误差的增大而降低;并且由于 GPS位置观测精度较低,造成INS惯性元件误差估计精度较低,INS误差错误修正,姿态角误差偏大;在两步自适应抗差 Kalman滤波中,由于一步滤波中利用了高精度的速度信息,导航精度受组合周期的长短、惯性元件误差的大小影响较小;而且在一步滤波中利用高精度的速度参数作为直接可测参数,INS误差得到很好的修正。另外,由于在两步自适应抗差Kalman滤波中采用自适应因子和等价权函数,既能控制扰动异常的影响也能抵制观测异常的影响。因此当GPS观测可用时,与伪距、伪距率紧组合Kalman滤波相比,采用两步自适应抗差Kalman滤波具有一定的优势。

[1] YANG Y.Tightly Coupled MEMS INS/GPS Integration with INS Aided Receiver Tracking Loops[D].Calgary: University of Calgary,2008.

[2] ALBAN S,AKOS D M,ROCK S M.Performance Analysis and Architectures for INS-aided GPS Tracking Loops [C]∥ION NTM.Anaheim:[s.n.],2003:611-622.

[3] WANG J H.Intelligent MEMS INS/GPS Integration for Land Vehicle Navigation[D].Calgary:University of Calgary,2006.

[4] SUN Zhengming,GAO Jingxiang,WANG Jian.Discussion on Weighting Factors of GPS Dual Frequency Phasesmoothed Pseudo-range[J]. Hydrographic Survey and Charting,2007,27(4):13-16.(孙正明,高井祥,王坚. GPS双频相位平滑伪距权重因子的探讨[J].海洋测绘, 2007,27(4):13-16.)

[5] YANG Yuanxi.Properties of the Adaptive Filtering for Kinematic Positioning[J].Acta Geodaetica et Cartographica Sinica,2003,32(3),189-192.(杨元喜.动态定位自适应滤波解的性质[J].测绘学报,2003,32(3):189-192.)

[6] YANG Yuanxi,HE Haibo,XU Tianhe.On Adaptively Kinematic Filtering[J].Acta Geodaetica et Cartographica Sinica,2001,30(4):293-298.(杨元喜,何海波,徐天河.论动态自适应滤波[J].测绘学报,2001,30(4): 293-298.)

[7] GAO Weiguang,YANG Yuanxi,ZHANG Shuangcheng. Adaptive Robust Kalman Filtering Based on the Current Statistical Model[J].Acta Geodaetica et Cartographica Sinica,2005,35(1):15-18.(高为广,杨元喜,张双成.基于当前加速度模型的抗差自适应Kalman滤波[J].测绘学报,2005,35(1):15-18.)

[8] YANG Y,GAO W.A New Learning Statistic for Adaptive Filter Based on Predicted Residuals[J].Progress in Natural Science,2006,16(8):833-837.

[9] CHAI Yanju.Theory and Method for Improving the Navigation Accuracy of GPS/INS Integration by Digging the Hidden Information[D].Wuhan:Institute of Geodesy and Geophysics,Chinese Academy of Sciences,2008.(柴艳菊.挖掘信息提高GPS/INS导航精度的理论与方法研究[D].武汉:中国科学院测量与地球物理研究所,2008.)

[10] DONG Xurong,Zhang Shouxin,Hua Zhongchun.GPS/ INS Integrated Navigation and Its Application[M]. Changsha:NationalDefence Scienceand Technology University Press,1998.(董绪荣,张守信,华仲春. GPS/INS组合导航定位及其应用[M].长沙:国防科技大学出版社,1998.)

[11] WANG Huinan.GPS Navigation Principal and Its Application[M].Beijing:Science Press,2003:206-241.(王惠南.GPS导航原理与应用[M].北京:科学出版社,2003: 206-241.)

[12] DENG Zili.Optimal Filtering Theory and Its Application—The Time Series Analysis[M].Harbin:Harbin Industry University Press,2000.(邓自立.最优滤波理论及其应用——现代时间序列分析方法[M].哈尔滨:哈尔滨工业大学出版社,2000.)

[13] GODHA S.Performance Evaluation of Low Cost MEMSBased IMU Integrated with GPS for Land Vehicle Navigation Application[D].Calgary:University of Calgary,2006.

[14] EUN-HWAN SHIN.Accuracy Improvement of Low Cost INS/GPS for Land Applications[D].Calgary:University of Calgary,2001.

[15] YANG Yuanxi.Theory and Application of Robust Estimation[M].Beijing:Bayi Press,1990.(杨元喜.抗差估计理论及其应用[M].北京:八一出版社,1990.)

[16] YANG Y.Estimators of Covariance Matrix at Robust Estimation[J]. ZeitschriftfuerVermessungswesen, 1997,122(4):166-174.

(责任编辑:丛树平)

A New Two-Step Adaptive Robust Kalman Filtering in GPS/INS Integrated Navigation System

WU Fumei1,2,Y ANG Yuanxi2
1.Institute of Surveying and Mapping,Information Engineering University,Zhengzhou 450052,China;2.Xi’an Research Institute of Surveying and Mapping,Xi’an 710054,China

In tight integrated navigation based on pseudorange and doppler observation,the precision is poor and the modification of the attitude errors is not accurate for poor observation precision of pseudorange.So a two-step adaptive robust Kalman filtering based on the observability of the parameters is presented.First the process of the tight integration is given and then the formulas and the approaches of the new method are deduced and analyzed. Finally an actual calculation is given.It is shown that compared with tight integration,the two-step adaptive robust Kalman filtering can control the disturbances of the state and the outliers of the observation.And the navigation precision does not decrease while the integration period becomes longer and the INS errors become bigger.The INS errors can be rightly estimated and the precision of attitude angles is improved.

two-step adaptive robust Kalman filtering;GPS/INS integrated navigation;tight integrated navigation; adaptive factor

WU Fumei(1981—),female,PhD candidate,majors in kinematic geodetic data processing.

E-mail:wfm8431812@163.com

1001-1595(2010)05-0522-06

P228

A

国家自然科学基金(40774001,40841021,40604003);国家863计划(2007AA12Z331);卫星导航与定位教育部重点实验室(B类)开放基金

2009-07-20

2009-08-31

吴富梅(1981—),女,博士生,主要从事动态大地测量数据处理。