导航用海洋重力异常图的孔斯曲面重构方法

李姗姗,吴晓平,赵东明

信息工程大学测绘学院,河南郑州450052

导航用海洋重力异常图的孔斯曲面重构方法

李姗姗,吴晓平,赵东明

信息工程大学测绘学院,河南郑州450052

基于地球重力物理场连续的特性,将计算机构图中的孔斯(Coons)曲面建模引入到导航用海洋重力异常图的加密重构中,建立不同边界曲线的双一次Coons曲面和双三次C1Coons曲面重力异常模型。通过对实验区数据计算分析,结果表明基于Coons曲面建立的重力异常模型精度均优于移动曲面拟合模型;同时利用现有全球SRTM30″plus海深数据,借鉴于间接内插的思想,以布格异常基于Coons曲面进行重力异常图的重构,与空间重力异常直接建模相比,精度整体提高25%。

重力异常图;双一次Coons曲面;双三次C1Coons曲面;布格异常

1 引 言

水下重力辅助导航是利用重力场信息来修正惯导随时间积累的定位误差。它要求首先将重力异常分布图存储在导航系统中,然后再依据重力传感器观测的重力场特征值通过最优化方法和卡尔曼滤波技术与重力图数据进行搜索匹配,以使水下潜器确认、跟踪、到达预期目的点,从而实现水下潜器的精确导航[1-2]。

在水下重力辅助惯性导航中,重力图一般是以规则格网的数字形式事先存储于匹配计算机中,以格网中点重力异常值表征。而水下潜器沿航迹方向的重力传感器的采样,即用于匹配的重力异常观测量并不一定是格网中点的重力值,以其作为格网平均重力异常进行重力图的搜索定位而发生的误匹配的概率随着代表误差的增大而提高。根据亨特代表误差经验公式[3]

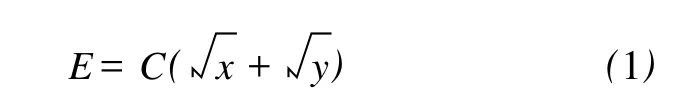
其中,E、C为代表误差和代表误差系数;x、y是格网边长。显然在同等水下地理环境下,重力图格网分辨率越大,则代表误差越大,发生误匹配的几率也越高。目前国内外利用 Geosat、Seasat、ERS-1和T/P等卫星测高数据依据逆Stokes公式、逆Vening-Meinesz公式基于 FFT算法建立了海洋区域2′×2′的格网重力异常模型[4-7],从式(1)可以近似地估计出当海洋区域重力异常格网分辨率提高至0.2′×0.2′时,代表误差大约降为原来的1/3,误匹配发生的几率也随之降低。因此高精度、高分辨率海洋重力异常图的获取是进行准确匹配定位的前提。

1967年美国麻省理工学院Coons S A提出了一种曲面分片、拼合造型的思想[8]。它是一种通过连接若干曲面片构造并组成任意复杂曲面的建模方法,每个曲面片由给定的四条边界曲线组成,由于与上、下、左、右四个相邻曲面片有公共线及公共点,因此能够保证曲面间的光滑拼接。与Bézier曲面、B样条曲面相比,其优点在于能够通过线构造曲面形成精确连续的平滑曲面[9]。由于重力异常物理场具有连续分布的特性,因此本文将在现有2′×2′格网数据的基础上基于Coons曲面提出一种新的导航用海洋重力异常模型插值重构的方法。

2 双一次Coons曲面重力异常模型

设有二元函数 f(x,y),区域Ω是分辨率为d的矩形格网单元,(x,y)∈Ω。如果Coons曲面插值于 x、y两个方向的四条边界曲线fx0、fxd、f0y、fdy,如图 1,则由此确定的双一次 Coons曲面为[8-11]

其中,

插值算子取为一次线性函数

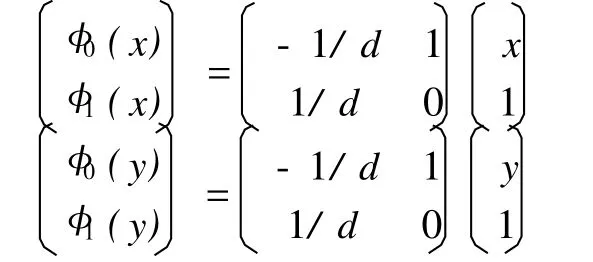
Coons曲面可以是由任意类型的四条边界曲线所构造的曲面,本文采用拉格朗日插值多项式构造四条边界曲线方程。

图1 边界曲线构成的曲面单元Fig.1 Curved surface cell constructed by boundary curves

如果四条边界曲线分别过相应的已知格网两点的重力异常值,则由拉格朗日插值公式可得

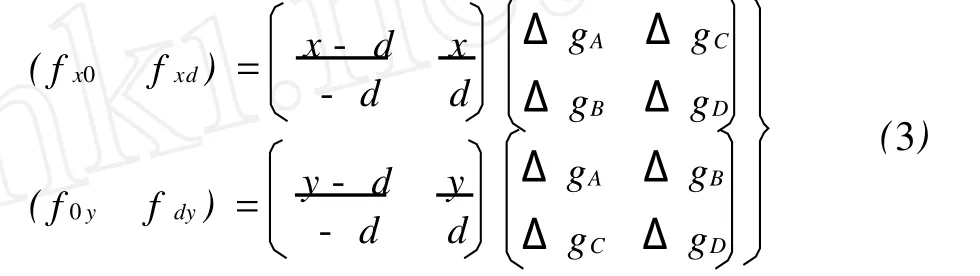
将式(3)代入Coons曲面模型中,得

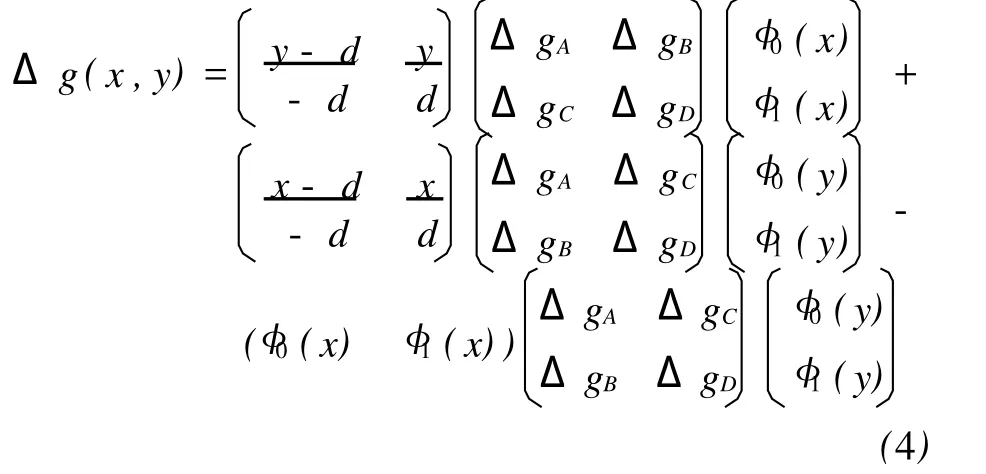
代入线性插值算子,式(4)整理为

显然该模型实质等价于双线性重力异常内插模型,因此可以说双线性内插模型是Coons曲面重力异常模型的特例。

同理,如果四条边界曲线分别过相应的已知格网三点的重力异常值,则可得边界曲线为二次曲线的Coons曲面重力异常模型

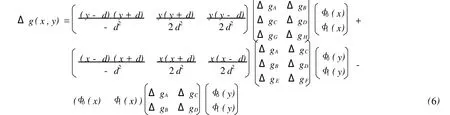
记为Coons model-A。

如果四条边界曲线分别由四个格网点所对应的重力异常值求得,则可得三次曲线的Coons曲面重力异常模型

记为Coons model-B。

加权二次曲线是通过过不同三点的两条二次曲线的加权平均来获取边界曲线方程。相对于三次多项式曲线,尽管也用到四点重力异常,但曲线方程的幂次却降低了一次。对于高次多项式而言,无疑避免了由于次数太高而产生的龙格现象。边界曲线为加权二次曲线的Coons曲面重力异常模型为

记为Coons model-C。

3 基于Coons曲面的海洋重力异常图数据的重构

已知某海域重力异常网格间距2′×2′,如图2所示。取其中1°×1°范围的重力异常作为实验区域,利用前面建立的4种双一次Coons曲面重力异常模型进行0.2′×0.2′重力异常图数据的重构,结果如图3所示。

图2 某海域2′×2′重力异常变化/(10-5ms-2)Fig.2 Variations of 2′×2′ocean gravity anomaly /(10-5ms-2)

图3 不同Coons曲面重力异常模型建立的0.2′×0.2′网格重力异常Fig.3 0.2′×0.2′grid gravity anomaly constructed based on different Coons curved surface

为了定量评价内插结果,利用不同Coons曲面以及移动二次曲面最小二乘拟合(曲面拟合所用点数与Coons model-B相同)建立的0.2′×0.2′网格重力异常模型,均采用加权平均求取2′×2′格网节点处的重力异常值,以节点处已知重力异常作为真值,两者求差,进行精度评定,结果见表1。

表1 不同Coons曲面重力异常模型精度Tab.1 Accuracy of different Coons curved surface /(10-5ms-2)

从表1可以看出,Coons曲面重力异常模型精度均优于移动曲面重力异常模型精度。这是因为Coons曲面重力异常模型是基于同侧格网点重力异常,依据重力异常起伏变化趋势构造最佳逼近曲线拟合重力异常剖面曲线,进而以最佳逼近曲线为边界曲线来调控整个插值曲面的形状与趋向,这与移动曲面直接基于离散格网点拟合构造重力异常模型相比,相当于在离散格网数据的基础上追加了一定的边界条件,因而使得精度有所提高;同时由于Coons model-A、Coons model-B、Coons model-C较之于双线性内插增加了已知网格点数,因而内插精度有所改进。但基于拉格朗日多项式建立的边界曲线方程,当所用网格点数越多,则幂次越高,有可能产生震荡现象,因此可采用加权等手段适当地降低幂次,既保证精度的提高,又可保证多项式的稳定。

4 基于海深数据的重力异常图数据重构

因为空间重力异常与地形具有强相关性,所以可以考虑采用与地形相关性弱的布格异常或均衡异常来进行曲面建模以提高精度。目前海洋区域已建立了30″×30″海深数据模型,与全球陆地SRTM地形数据一起形成了全球SRTM30″plus地形数据模型。因此基于高于现有海域重力异常2′×2′分辨率的地球物理信息-海深数据来获取更高分辨率及更高精度的重力异常模型从理论上来说是可行的。在海洋重力学中,布格异常表示为[12]

式中,ΔgB、Δg表示布格异常和空间异常;G是万有引力常数;δ、δ0是地壳平均密度与海水密度;h为测点水深;h′为瞬时潮高;最后一项很小,一般予以忽略。

此外由于由回声测深仪获取的水深测量值受声速的影响,在水深3 000 m的海区引起布格异常的变化有3×10-5ms-2左右,因此还要加入相应的声速改正。此次用于实验的海深数据改正式为[12]

图4是SRTM30″plus提供的实验区30″× 30″的海深数据,其变化态势与实验区空间异常的变化态势(见图2)基本一致,海深数据变化剧烈的区域相应的空间异常也变化剧烈。图5是依据式(9)计算的实验区布格异常,明显受海深影响小,变化比空间异常平缓的多。

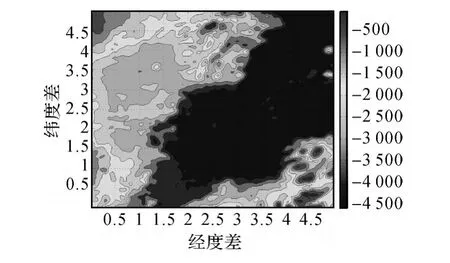
图4 实验区30″×30″海深数据/mFig.4 30″×30″ocean depth data/m

图5 实验区布格异常/(10-5ms-2)Fig.5 Bouger gravity anomalies/(10-5ms-2)

图6是利用4种Coons曲面重力异常模型建立的 0.2′×0.2′网格布格异常。根据图 6与式(9)可以得到图7。显然图7与图3相比,重力异常图的细部特征更为明显,且比较表1、表2,基于海深数据的Coons曲面重力异常模型的精度整体约提高了25%。当曲面变化趋势平缓时,移动曲面拟合精度与双线性内插精度相当,但本文移动曲面拟合所用的已知格网点数是双线性内插所用点数的3倍,因此从性效比而言,仍认为Coons曲面重力异常模型精度优于移动曲面重力异常模型精度。

图6 利用4种Coons曲面重力异常模型建立的0.2′×0.2′网格布格异常/(10-5ms-2)Fig.6 0.2′×0.2′grid Bouger anomaly using 4 Coons curved surface/(10-5ms-2)

图7 基于海深数据利用4种Coons曲面重力异常模型建立的0.2′×0.2′网格重力异常/(10-5ms-2)Fig.7 0.2′×0.2′grid gravity anomaly using 4 Coons curved surface based on ocean depth data/(10-5ms-2)

表2 基于海深数据的4种Coons曲面重力异常模型精度Tab.2 Accuracies of 4 Coons curved surface gravity anomaly based on ocean depth data /(10-5ms-2)

5 双三次C1Coons曲面重力异常模型

5.1 双三次C1Coons曲面

双三次C1Coons曲面插值于四条边界曲线及边界曲线的跨界切矢。设给定的插值条件为四条三次边界曲线 fx0、fxd、f0y、fdy及 fdy以及四条边界曲线跨界切矢 dyfx0、dyfxd、dxf0y、dxfdy,如图8,则由此确定的双三次Coons曲面为

其中,

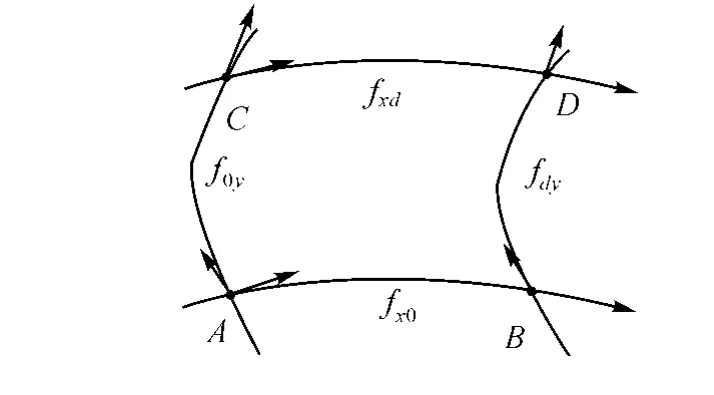
图8 边界曲线及边界曲线跨界切矢Fig.8 Boundary curves and their crossing boundary tangent vectors

令插值函数为三次埃尓米特基函数

显然相比于双一次 Coons曲面,双三次C1Coons曲面的相邻小的两曲面之间除了有公共线与公共角点外,还必须保证跨界切矢、扭矢在四个角点处满足相容性[8]。

5.2 边界曲线跨界切矢的确定

根据Farin G给出的确定双三次Coons曲面片边界曲线跨界切矢的方法[13],利用四个角点的跨界切矢与跨界扭矢值来生成四条边界曲线的跨界切矢。

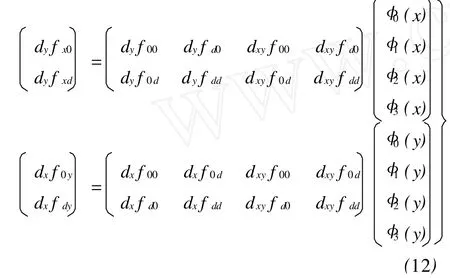
5.3 角点跨界扭矢值的确定[14]

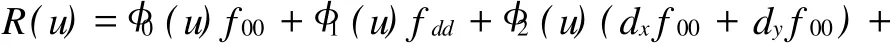
采用使曲线 R(u)和U(s)的应变能最小的原则来确定函数值Q,得

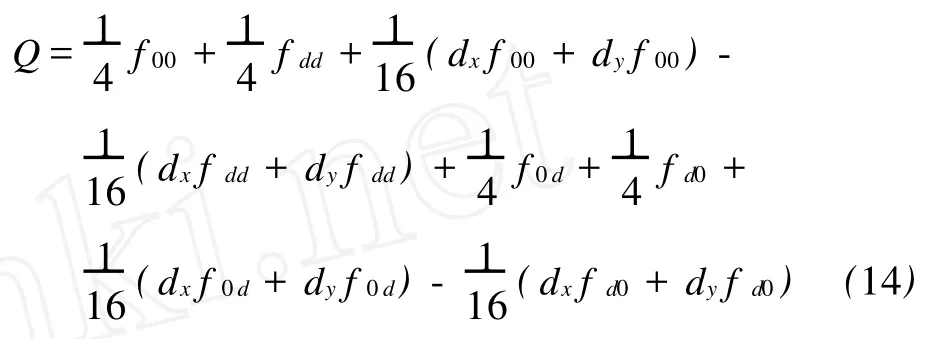
代入式(13),可求出 R(u)与U(s)。因此四个角点的扭矢分别为

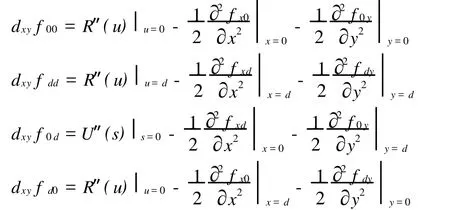
5.4 双三次C1Coons曲面重力异常模型

边界曲线采用拉格朗日插值三次多项式,由此所得的基于埃尔米特插值算子双三次C1Coons曲面重力异常模型

记为C1Coons model-D。

5.5 实验数据计算分析

取某海域20′×20′范围的2′×2′重力异常,利用双一次Coons曲面和双三次C1Coons曲面重力异常模型进行0.2′×0.2′重力异常图的重构,结果如图9、表3所示。

图9 双一次Coons曲面和双三次C1Coons曲面重力异常模型建立的0.2′×0.2′网格重力异常Fig.9 0.2′×0.2′grid gravity anomaly using bilinear Coons and bi-cubic C1Coons curved surfaces

表3 双一次Coons曲面和双三次C1Coons曲面重力异常模型精度Tab.3 Accuracy of grid gravity anomaly using bilinear Coons and bi-cubic C1Coons curved surfaces /(10-5ms-2)

双三次C1Coons曲面重力异常模型,因为各个相邻小曲面之间除了有公共边界与角点外,还保证了跨界切矢与扭矢在四个角点处的相容性,因此比双一次Coons曲面重力异常模型的插值精度高。从表3可以看出,其建立的重力异常模型精度比双一次Coons曲面重力异常模型精度约提高了10%。

6 结 论

建立精度与密度均满足要求的海洋重力异常图是将重力无源导航应用于实际需解决的关键问题。本文在现有海洋2′×2′重力图数据的水平下,提出了基于Coons曲面的海洋重力异常图重构方法,建立了双一次和双三次Coons曲面重力异常模型,较之于移动曲面拟合,精度均得到了有效提高;研究了先利用30″×30″海深信息建立0.2′×0.2′Coons曲面网格布格异常,再减去布格改正的影响从而得到0.2′×0.2′网格空间异常,与空间异常基于Coons曲面的直接建模,精度整体提高了25%。同时通过实验计算发现:对于重力异常变化剧烈的海域,较为适宜采用二次加权曲线的双一次Coons曲面重力异常模型,在保证精度的同时又避免了基于拉格朗日多项式的边界曲线方程出现龙格现象;双三次C1Coons曲面较之于双一次Coons曲面虽然计算精度有所提高,但涉及曲线跨界切氏与扭氏的计算,建模速度较慢,不适合进行大区域海洋重力异常图的加密重构。

值得指出的是,建立高精度、高分辨率的导航用重力异常图,一个好的数学推值方法固然重要,但观测数据本身的质量、分布及疏密程度也是决定重力异常图精度的重要因素。目前获取海洋重力数据的主要手段有卫星测高、航空和船载重力测量,各种测量数据的处理以及相互融合手段也是获取理想观测数据质量及分布结构的重要研究问题。一个好的数据结构结合一个好的数学方法,有望得到更高精度及分辨率的海洋重力异常图,从而提高重力辅助惯性导航的匹配精度。

[1] JIRCITANO A,DANIEL E D.Gravity Aided Inertial Navigation System[C]∥Proceedings of ION 47th Annual Meeting.Washington DC:Institute of Navigation,199l: 221-229.

[2] RICE H,MENDELSOHN L,AARONS R,et al.Next Generation Marine Precision Navigation System[C]∥IEEE 2000 Position Location and Navigation Symposium.San Diego:IEEE,2000:200-206.

[3] HEISKANING W A,MORITZ H.Physical Geodesy[M]. Beijing:Surveying and Mapping Press,1984.(W A海斯卡涅,H莫里兹.物理大地测量学[M].北京:测绘出版社,1984.)

[4] ANDERSON O,KNUDSEN P.Global Marine Gravity Field from the ERS-1 and Geosat Geodetic Mission Altimetry[J].J Geophys Res,1998,103(C4):8129-8137.

[5] HW ANG,C W,KAO,E-C,PARSONS B.Global Derivation of Marine Gravity Anomalies from Seasat,Geosat, ERS-1 and TOPEX/Poseidon Altimeter Data[J].Geophysical Journal International,1998,134(2):449-459.

[6] SANDWELL D,SMITH W.Marine Gravity Anomaly from Geosat and ERS-1 Satellite Altimetry[J].J Geophys Res,1997,102(D10):10039-10054.

[7] HUANG Motao,ZHAI Guojun,GUAN Zheng,et al.On the Recovery of Gravity Anomalies from Altimeter Data [J].Acta Geodaetica et Cartographica Sinica,2001,30(2): 179-184.(黄谟涛,翟国君,管铮,等.利用卫星测高数据反演海洋重力异常研究[J].测绘学报,2001,30(2): 179-184.)

[8] COONS S A.Surfaces for Computer Aided Design of Space Forms[R].Cambridge:MIT,1967.

[9] WANG Yaoge,ZHU Changqing,WANG Zhiwei.A Surface Model of Grid DEM Based on Coons Curved Surface[J]. Acta Geodaetica et Cartographica Sinica,2008,37(2):217-222.(王耀革,朱长青,王宗伟.基于Coons曲面的规则格网DEM表面模型[J].测绘学报,2008,37(2):217-222.)

[10] WU Zhongming.Model,Method and Theory of Scattering Data Fitting[M].Beijing:Science Press,2008.(吴宗敏.散乱数据拟合的模型、方法和理论[M].北京:科学出版社,2008.)

[11] HU Peng,YANG Chuanyong,WU Yanlan,et al.New Digital Elevation Model[M].Beijing:Surveying and Mapping Press,2007.(胡鹏,杨传勇,吴艳兰,等.新数字高程模型[M].北京:测绘出版社,2007.)

[12] HUANG Motao,ZHAI Guojun,GUAN Zheng,et al.Surveying of Ocean Gravity Field and Applications[M].Beijing: Surveying and Mapping Press,2005.(黄谟涛,翟国君,管铮,等.海洋重力场测定及其应用[M].北京:测绘出版社,2005.)

[13] FARIN G.Curves and Surfaces for Computer Aided Geometric Design:A Practical Guide[M].New York:Academic Press,1988.

[14] CHEN Hui,ZHANG Caiming.A Method of Determining Twist in Constructing C1Coons Surface to Interpolate Boundary Curves[J].College Journal of Applied Mathematics:A,1998,13(Sup):79-85.(陈辉,张彩明.用边界曲线构造C1Coons曲面确定扭矢的方法[J].高校应用数学学报:A辑,1998,13(增刊):79-85.)

(责任编辑:丛树平)

Coons Curved Surface Reconstruction Method of Marine Gravity Anomaly Map for Navigation

LI Shanshan,WU Xiaoping,ZHAO Dongming
Institute of Surveying and Mapping,Information Engineering University,Zhengzhou 450052,China

Based on the continuation property of the Earth’s gravity field,the Coons curved surface modeling of computer graphics was introduced into the reconstruction of the marine gravity anomalies map for navigation,and both the bilinear Coons curved surface gravity anomaly model and bi-cubic C1Coons curved surface gravity anomaly model for different boundary curves were established.Through the analysis of data within experimental area, results showed that the accuracy of gravity anomaly model based on Coons curved surface was better than that based on moving surface fitting model.Based on the global SRTM30″plus oceanic depth data,the reconstruction of gravity anomaly map based on Coons curved surface using Bouger anomaly was made,and the accuracy was improved by 25%compared with the direct modeling using free air gravity anomalies.

gravity anomaly map;bilinear Coons curved surface;bi-cubic C1Coons curved surface;Bouger anomaly

LI Shanshan(1970—),female,associate professor,PhD candidate,majors in physical geodesy.

E-mail:zzy_lily@sina.com

1001-1595(2010)05-0508-08

P223

A

全国优秀博士学位论文作者专项基金(200344);国家自然科学基金(40774031)

book=515,ebook=262

2009-09-23

2010-04-05

李姗姗(1970—),女,副教授,博士生,研究方向为物理大地测量。