在时间窗条件下应急物资运输路径优化问题研究

陈钢铁，帅 斌

（西南交通大学 交通运输学院，四川 成都 610031）

城市应急系统的一项重要任务就是决定城市应急运输路线，要求发生事故时，救援者能以最快的速度到达现场进行救援。传统的车辆路径问题(Vehicle Routing Problem，VRP)是为运输物资的车辆设计最佳路径，使其总运输费用最小。这个问题是Dantzig和Ramser在解决一个实际汽油运输问题时提出的[1]。Toth 和Vigo、Laporte建立了多种变形的VRP模型，如有时间窗的VRP模型，有多个供应点的VRP模型，动态选择路径的VRP模型，并给出了相应的算法[2-3]。与传统的VRP相比，应急物资调运主要是应急车辆在最短的时间内把应急物资由应急服务点运送到需求点，其研究的核心是最短路径选择问题。近年来，随着应急管理的推广实施，应急物资调度中的车辆路径选择与优化，成为该领域的一个新的热点。在应急情况下，由于可选择的路径有限，因此需要研究在最短的时间求得最优化的路径。

1 问题描述

基于禁止时间窗的应急物资调度车辆路径问题，在对研究问题进行界定的基础上，构建问题的整数规划优化模型。在应急情况下，可供选择的路径不是很多，可以采用动态规划和标号法求解。采用这种算法能在短时间内为在时间窗条件下应急物资的运输路径优化求得最优解。最后通过实例计算对研究成果进行说明。

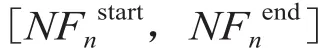
现假定在网络中的某一节点nacci发生一突发应急事件，需要从另节点nstor紧急调运应急物资。不失一般性，将运输车辆离开出发节点nstor的时间标记为基准时刻0，即nstor＝0，网络G中其他节点和枝线的禁止时间窗均基于该时刻进行定义。则本文所解决的问题就是在禁止时间窗限制下，从网络G中选择节点nacci到节点nstor的运输路径，使车辆到达应急事件发生节点的时间最少。

2 模型建立

由于网络路径由节点和枝线组成，因此通过定义两组决策变量来确定所选择的运输路径。

在上述定义的基础上，根据对问题的界定，可构建基于禁止时间窗的应急物资调度车辆路径问题优化模型为：

式中，Snstor和Snacci为节点nstor和nacci相连枝线的集合；nother为除nstor和nacci以外的其他节点；Snother为与节点nother相连枝线的集合；和为运输车辆在枝线a上的进入和离开节点。

上述优化模型为一个整数规划模型。目标函数⑴式为最小化运输车辆到达应急事件发生地的时间。⑴式等号右边第一项为运输车辆在所选路径上各节点的等待时间；第二项为运输车辆在各枝线的等待时间与行驶时间之和。

约束条件⑵式包含有两个式子，第一个是确保应急物资存储地点和应急事件发生地点都位于所选路径上；第二个是保证在与起始节点和终止节点相连的所有枝线中，有且只有一条被选中。约束条件⑶式是一个路径连通性约束，包含有两个式子，第一个是当某一枝线被选中时，其两端的两个节点同时被选中；第二个是确保当某一节点(nstor和nacci除外)被选中时，与其相连的枝线中有且只有两条被选中。约束条件⑷式是车辆运输时间递推约束，包含有两个式子，第一个将运输车辆离开应急物资存储地点的时刻定义为0；第二个是通过与节点相连的枝线，将车辆运输时间由某一个节点递推到与其相邻的下一个节点。约束条件⑸式是等待时间约束，通过这两个式子可分别计算出由于禁止时间窗的限制，运输车辆在某一节点或枝线的等待时间。约束条件⑹式为决策变量的定义域约束。

3 模型算法

对于时变条件下有时间窗最短路径动态优化问题，可以采用动态规划和标号法求解。一般对于一个运输网络，在求解过程中可以将其划分成若干阶段，以起始阶段由前向后逐段推移，直到最后一个阶段结束为止。

为了获得各个目标值和相应的概率，首先，第一层确定时间组合；然后，第二层确定目标组合，获得期望目标值。因此，对于任意一个节点 j 赋以两个标号，标号1是确定了时间组合时所获得的目标值、概率和时间，；标号2是所有时间组合下的目标值。在此，对于任意一个节点 j 均赋以标号q−1)]和标号其中，q为节点 j 的所属段；为节点 j 在阶段 q 的时间组合；q－1为节点 i 的所属的阶段；为节点i在阶段q－1的时间组合；Zj为时间组合在从节点 j 出发时各个目标的期望值，)；Pj为时间组合在到达节点 j 时各个目标的概率，其中，是一个向量，表示在时间组合wtj,η下从节点 j 出发的时间；表示在时间组合下到达节点 j 的时间；EZj为选择了所有的时间组合后的期望目标值，是一个向量，)，为选择了所有的时间组合后目标h的期望值。其中，j∈N−{O}，(i ，j)∈E。

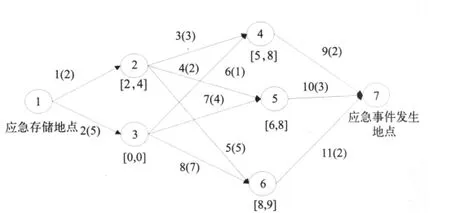
图1 网络运输图实例

4 实例计算

利用图1所示的实例对研究结果进行说明。图1中节点1和节点7分别为应急物资的储存地点和应急事件的发生地点，节点和枝线的代号用数字表示，其禁止时间窗标注在节点代号的下部，枝线代号后圆括号中的数字为车辆在该枝线上的行车单位时间，利用动态规划和标号法求解该实例。

车辆沿着“节点1→枝线1→节点2→枝线3→节点4→枝线9→节点7”将应急物资从储存地点运送到事发地点，所消耗的总时间为10。这是从应急存储地点到应急事件发生地点的最短时间。

车辆先从应急存储地点节点1出发，选择枝线1，经过2个单位时间行驶到节点2，在该节点上需要等待2个单位时间后(禁止时间窗为[2，4])，选择枝线3，经过3单位时间行驶后，于7个单位时间到节点4，在该节点上需要等待1个单位时间后(禁止时间窗[5，8])，选择枝线9，经过2个单位时间，于10个单位时间到达节点7应急事件发生地点。

5 结束语

带有禁止时间窗的应急物资调度车辆路径问题，只考虑时间窗条件下对应急物资和救援的路径的优化，而在现实生活和情景中有很多不确定因素对应急路径优化产生影响，因此对于在多个不确定因素条件下应急路径优化需要进一步的研究。在应急路径中更复杂的网络问题、路径优化及其相关的算法也是进一步研究的方向。

：

[1] Dantzig G B，Ramser J H. The Truck Dispatching Problem[J].Management Science，1959，6(1)：80-91.

[2]Toth P，Vigo D. The Vehicle Routing Problem，SLAM Monographs on Discrete Mathematics and Application[M].SLAM Publishing，2002.

[3] Laporte，G. The Vehicle Routing Problem，An Overview of Exact and Approximate Algorithms [J]. European Journal of Operations Research，1992(59)：345-358.