思维品质数字化的个案研究
2010-09-04田果萍崔克忍
田果萍,崔克忍
(1.山西大同大学数学与计算机科学学院,山西大同 037009;2.山西师范大学数学与计算机科学学院,山西临汾 041004)
思维品质数字化的个案研究
田果萍,崔克忍
(1.山西大同大学数学与计算机科学学院,山西大同 037009;2.山西师范大学数学与计算机科学学院,山西临汾 041004)
对思维能力的训练突出地体现在数学的教学中,思维品质是衡量个体思维能力的重要指标,文章在思维品质数字化理论模式的构建之上,旨在通过例子展示出思维品质数字化的具体的操作流程.
思维品质 数字化 流程
思维是“智力与能力的核心”[1],“思维品质是思维能力强弱的反映”,“培养思维品质是发展智力、能力的突破口,是提高教育质量的好途径”[2],尤其是数学教学,“数学思维的价值在于培养良好的思维品质,这是大家公认的”[3].而以往关于思维品质方面的文献,大多或侧重于数学课堂教学的培养策略的视阈,“你想要讲的,尽量启发、诱导学生去思索,用学生的口说出你想要说的话,有时学生也能说出教师料想不到的新见解。通过师生之间的信息交换,使学生的思维品质得到培养”[4]、“数学教材中有着丰富的培养学生思维能力的素材和方法,选择其中的有关例题、习题,引导学生观察、分析其特点,然后精心设置教学程序,展现结论形成的过程,让学生充分参与,积极探索,他们的抽象以至归纳等思维能力即可得以较好的发展”[5];或者对思维品质的教育意义讨论的居多,如“思维品质是数学素质不可或缺的内容”[6],而基于从数学函数的观点来量化思维品质,除了孟凯韬教授之外,未见他人有相关的研究,本文基于作者对思维品质数字化理论模式构建[7]的基础上,旨在通过具体的例子展示出思维品质数字化的操作流程.
1 解题过程及其思维网络图
下面以高中数学数列中的一道题为例来说明具体操作步骤.
题目 已知数列{an}的前n项和为Sn,且an是Sn与2的等差中项;数列{bn}中,b1=1,点p(bn, bn)在直线x-y+2=0上,其中n∈N*.
(1)求数列{an}与{bn}的通项公式;
(2)设数列{bn}的前n项和为Bn,试比较1/B1+1/B2+…+1/Bn与2的大小;
(3)设Tn=b1/a1+b2/a2+bn/an,若Tn≺c,c∈Z,求c的最小值.
某同学的解题步骤是:
(1)由题意可得an=(Sn+2)/2,从而
Sn=2an-2.
当n=1时,
a1=(S1+2)/2⇒ a1=2,
当n≠1时,
an=Sn-Sn-1=2an-2-(2an-1-2)=2an-2an-1,
所以,an=2an-1,从而an/an-1=2.故数列{an}是首项为2,公比为2的等比数列且
an=a1·qn-1=2n.
数列{bn}中,由题意可得
bn-bn+1+2=0,
即
bn+1-bn=2,
所以{bn}是首项为1,公差为2的等差数列,且


故Tn<3(n→∞).
又c∈Z,故cmin=3.
其思维网络图如图1.

图1 思维网络图
图1中各元素所代表的意义:
①an是Sn与2的等差中项;
②2an=Sn+2;
③Sn=2an-2;
④当n=1时a1=2;
⑤利用an=Sn-Sn-1;
⑥利用n的意义;
⑦ an=2an-1;
⑧利用公式an=a1·qn-1;
⑨an=2n;
⑩已知p(bn,bn)在直线x-y+2=0上;
(11)bn-bn+1+2=0;
(12)bn+1-bn=2;
(13)已知b1=1;
(14)利用公式bn=b1+(n-1)d;
(15)bn=2n-1;
(16)Bn=n2;
(17)当n=1时B1=1<2;
(18)当n≠1时;
(19)利用放缩法;
(20)∑1/Bi<2;
(21)得出结论;∑1/Bi<2;
(22)Tn表达式;
(23)1/2 表达式①;

(25)对Tn求极限;
(26)Tn<3;
(27)c∈Z;
(28)得出结论cmin=3.
2 各项思维品质的值
2.1 思维创新性
根据提供的信息知t=15min;
1)为方便起见,不妨以一个信息加工过程中的终点思维元素来代表一个思维环节,则所有思维环节如下:
②③④⑦⑨(11)(12)(15)(16)(17)(18)(19)(20)(21)(22)(23)(24)(25)(26)(28)共19个,所以
2)tc(v)=19÷15=1.2667;
3)本题得以正确解决,虽然与每一个思维环节均有关系,缺一不可,但起关键作用的,能保证思维过程得以流畅的思维环节(仍然以每个思维环节的终点元素来表示)有:
②③④⑦⑨(12)(15)(16)(20)(22)(23)(24)(25)(26)(28),
也就是说这些思维环节产生了积极的效果,对于中学生来讲我们认为凡凭借自己的头脑所获得的一切知识都是具有发现意义的,是具有创造性的.因此,思维链中所含创造性思维环节的个数为15个,即
ootc(x-f-y)=15;
4)citc(x-f-y)=15÷19=0.7895;
5)eftc(x-f-y)=15÷192=0.0416;
6)actc(x-f-y)=0.5eftc(x-f-y)+0.5tc(v)=0.6541.
2.2 思维的新颖度
7)本题得以顺利完成既有赖于严谨的逻辑思维,又得力于能够展开丰富的联想.从思维网络图中可以看到有些想法比较新奇,其新奇程度可根据如下的评分规则评定出每个思维环节的新颖度.评分规则如下:
(1)由已知能够直接导出明显的关系得0.1分;
(2)根据提示语能够导出正确的式子得0.2分;
(3)计算或推导准确的得分0.3分;
(4)能够准确写出所需公式的得0.4分;
(5)能够抓住公式各字母的本质含义或能够灵活运用公式变形的得0.5分;
lotc(x-f-y)=19;
(6)为达到一个目标能够挖掘出所需隐含条件的得0.6分;
(7)能够全面讨论问题各种情况的得0.7分;
(8)能够联想出已知元素之间关系的得0.8分;
(9)能够构造出一个铺垫的得0.9分;
(10)能够联想出一个恰当且简便方法的得1分.
按照上面的评分规则,每个思维环节的新颖度分别为
0.2 ,0.3 ,0.5,0.8,0.6,0.1,0.3,0.6,0.3,0.7,0.7,1,0.3,0.3,1,0.3,1,0.3,0.3,
所以其新颖度

2.3 思维的广度
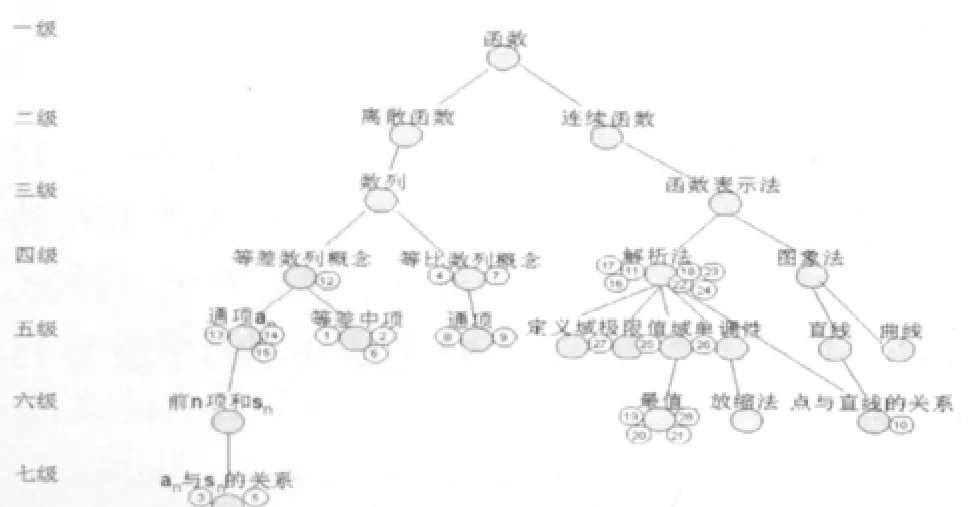
图2 系统套图
9)根据该同学的思维视野所涉及的范围,可以构造一个如图所示的系统套:图2从图中可以看到该系统套的相关p=7各级跨度依次为1,2,2,4,9,9,9,从而其跨度积
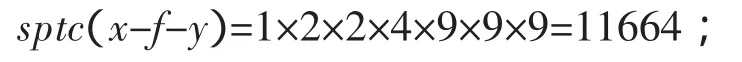
令m=2,n=5得思维广度为

2.4 思维的灵活度
10)以各个思维元素为横坐标,各个元素所属的级为总坐标建立如下直角坐标系:图3.

图3 :系统套的直角坐标系
由上图及拐点定义可知思维链的拐点;
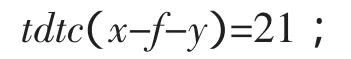
11)令m=3,n=2得到该同学的思维灵活性
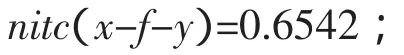
2.5 思维的深刻性
12)另外,从图3中还可以看到:
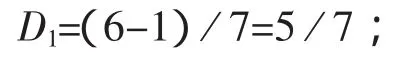
其中D1为“等差中项”与“点与直线的关系”的相对距离.
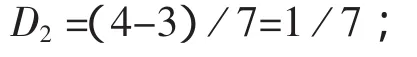
其中D2为“等差中项”与“等比数列概念”的相对距离.
从而该同学的思维深度为

3 思维品质函数的值
13)最后,令
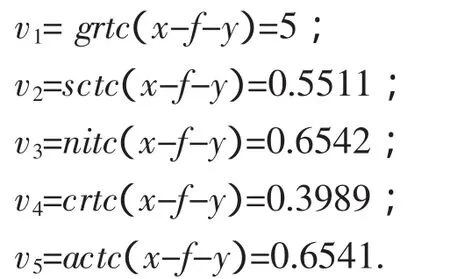
所以,思维品质向量为
(5,0.5511,0.6542,0.3989,0.6541),
将其以矩阵形式输入后,应用[4]中的计算程序即可得到该同学相应的思维品质函数值为
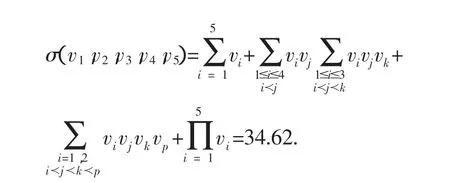
[1]林崇德.学习与发展-中小学心理能力发展与培养[M].北京:北京师范大学出版社,1999.
[2]胡卫平.科学思维培育学[M].北京:科学出版社,2004.
[3]张奠宙,李士琦,李俊.数学教育学导论[M].北京:高等教育出版社,2003.
[4]郝秀清.关于目前中专数学教学的现状及改革设想[J].北京师范学院学报,2001,17(2):43-44.
[5]王苗珍,杨清华.探讨例题习题规律[J].重视思维能力培养[J].雁北师范学院学报,2001,17(2):55-56.
[6]张计珍.数学教学中素质的培养[J].雁北师范学院学报,2004,20(2):83-84.
[7]田果萍.思维品质数字化的理论建构[J].山西师范大学学报:自然科学版,2008,24(2):21-23.
An Examp le for Digitalization of Thinking Quality
TIAN Guo-ping,CUIKe-ren
(1.School ofMathematics and Computer Science,ShanxiDatong University,Datong Shanxi,037009;2.School ofMathematics and Computer Science,ShanxiNormal University,Linfen Shanxi,041004)
Thinking is trained mostly in themathematics instruction.Thinking quality is treated as one of its value item.Basing on its theoreticalmodel,and by a concrete example,the operation process of the digitalization of thinking quality is displayed.
thinking quality;digitalization;process
G420
A
〔编辑 高海〕
1674-0874(2010)02-0018-04
2009-11-03
田果萍(1975-),女,山西朔州人,硕士,讲师,研究方向:数学课程与教学论.
