椭圆上二维均匀分布的参数估计

鲁富荣，张莉莉

（1.山西大学商务学院，山西太原 030600；2.山西农业大学文理学院，山西太谷 030801）

椭圆上二维均匀分布的参数估计

鲁富荣1，张莉莉2

（1.山西大学商务学院，山西太原 030600；2.山西农业大学文理学院，山西太谷 030801）

研究了椭圆上二维均匀分布的参数估计问题，得到了未知参数及区域面积的矩估计，并通过适当的变换，给出了参数的最大似然估计和区间估计.

二维均匀分布 矩估计 最大似然估计 区间估计

均匀分布是概率论中的一个常用分布.目前，有关区间［a，b］上一维均匀分布的研究已有很多成果，可查阅相关文献.对于二维均匀分布的研究，其成果主要有矩形区域和圆内二维均匀分布的参数估计及区域面积的估计，见文献 [1]～[3].但迄今为止，有关椭圆上二维均匀分布的相关研究还没有，而椭圆上二维均匀分布在物理[4]、军事等领域里有着广泛的应用.本文主要研究椭圆上二维均匀分布的参数估计问题，并给出了未知参数与区域面积的矩估计及参数的最大似然估计和区间估计.

1 定义及引理

定义［5］设G是平面上的有界区域，其面积为A.若二维随机变量（X，Y）有概率密度

则称（X，Y）在G上服从均匀分布.

注:当

证明 随机变量（X，Y）的概率密度函数为

注:本引理与文献［3］实际上是用不同方法证明出了相同的结论.

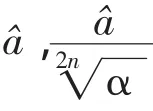
2 参数的矩估计

注:随机变量X与Y各自并不服从一维的均匀分布，且X与Y不相互独立.

所以椭圆半轴长a与b的矩估计量分别为

注:当a＝b时，可得服从圆x2-y2≤a2上均匀分布的二维随机变量，圆面积A＝πa2的矩估计量为

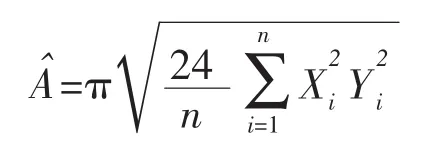
3 参数的最大似然估计

证明 随机变量(X,Y)的概率密度函数为

所以二维随机变量（X，Z）服从圆x2+z2≤a2上的均匀分布.

证明 由引理1和定理3证之.

4 参数的区间估计

证明 由引理2和定理4易证之.

综上，我们得到了椭圆上二维均匀分布未知参数及区域面积的矩估计，在椭圆两半轴长之比k已知的条件下还得到了参数的最大似然估计和区间估计.当这个比值未知时，可先由k的矩估计量代替，进而得参数的两步估计[6].

[1]金文奇.关于圆内均匀分布的检验与估计[J].兵工学报,2001,22(4):468-472.

[2]刘兆君.二维均匀分布矩形区域面积的估计[J].大学数学,2007,23(4):155-159.

[3]王志祥.圆内二维均匀分布的参数估计[J].大学数学,2008,24(2):150-152.

[4]胡熙静,刘桂贤.蒙特卡罗方法初步-椭圆内均匀分布的技巧[J].爆轰波与冲击波,1995,12(4):39-44.

[5]盛骤,谢式千,潘承毅.概率论与数理统计[M].3版.北京:高等教育出版社,2007.

[6]王松桂,史建红,尹素菊,等.线性模型引论[M].北京:科学出版社,2004.

Abatract：In this paper，we discuss the parameter estimation of two－dimensional uniform distribution on a ellipse.We obtain themoment estimator of the parameter and the region area，meanwhile，we give the parametric maximum likelihood estimation and interval estimation bymaking the appropriate transformation.

Parameter Estimation of Two－dimensional Uniform Distribution on a Ellipse

L U Fu－rong1，Zhang Li－li2
（1.Business College,ShanxiUniversity，Taiyuan Shanxi，030031）（2.College of Arts and Science，Shanxi Agricultural University，Taigu Shanxi，030801）

two－dimensional uniform distribution；momentestimation；maximum likelihood estimation；estimate interval

O212.1

A

〔编辑 高海〕

1674-0874(2010)04-0006-03

2009-05-10

山西大学商务学院科研基金资助课题［SD200963］

鲁富荣(1981-),男,山西河曲人，硕士,助教,研究方向：高等数学与图论.