一种变形蔡氏混沌吸引子的研究与电路实现
2010-09-04周武杰杨春亭
周武杰,杨春亭
(浙江科技学院信息与电子工程学院,浙江杭州310023)
0 引 言
近年来,混沌在数学、信息科学以及其它工程领域获得了国内外广泛的重视,成为了非线性学科的一个热点课题[1-6]。众所周知,蔡氏电路已成为了理论和实验研究混沌的一个范例[1,2]。在此基础上,人们还研究了蔡氏电路的其它形式,如多涡卷蔡氏电路、MCK电路、变形蔡氏电路、网格多涡卷蔡氏电路、高阶蔡氏多涡卷等电路[3-6]。特别是文献6报道了用阶跃函数序列构造了网格状蔡氏混沌吸引子,为研究蔡氏网格混沌吸引子打下了基础。在文献6的基础上,提出了一种变形的蔡氏网格多涡卷混沌系统。本文利用蔡氏电路的对偶性,交换状态方程右边等式的x和z,用z来构造非线性函数,再利用阶跃函数对y方向上的扩展指标2鞍焦点,在这个方向上可产生奇数或偶数个混沌吸引子,那么从z-y平面上看到的吸引子成网格状。对该系统进行计算机仿真,分析了系统的动力学问题,并对系统进行电路实验。从计算机模拟、理论分析和硬件实验,验证了系统的混沌特性。
1 一种变形的蔡氏网格多涡卷混沌系统动力学特性
1.1 变形蔡式多涡卷混沌系统的提出和计算机仿真
在文献6研究蔡氏电路的基础上,本文提出了一个新的变形蔡式网格多涡卷混沌系统,其状态方程可表示为:

式中,a=-10,b=-4~-6;f(z)为三角波函数序列,其数学表达式为:
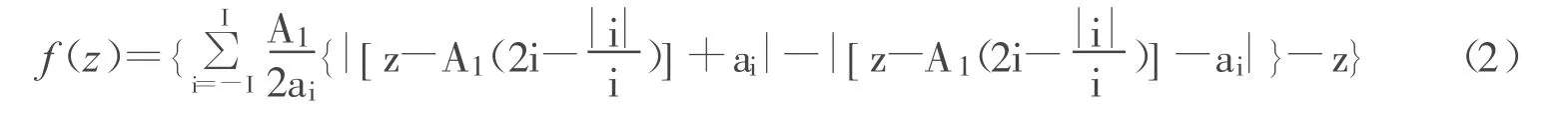
式中,A>0和ai∈(0,A](i=±1,±2,…,±I)称为三角波参数,ai又称三角波的相对转折点值,I为
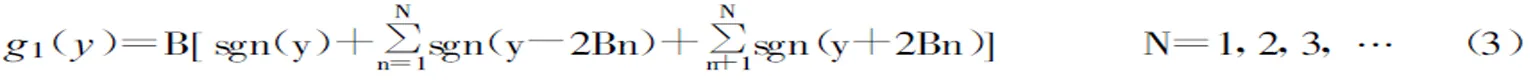
为使式1在 y方向上产生具有奇数个涡卷的多涡卷混沌吸引子,构造阶跃函数序列 g(y)=g2(y),其一般数学形式为:正整数。利用式2,可产生一维2I+1涡卷混沌吸引子。
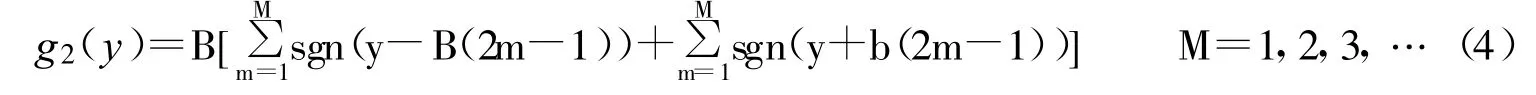
为使式1在y方向上产生具有偶数个涡卷的多涡卷混沌吸引子,构造阶跃函数序列g(y)=g1(y),其一般数学形式为:
式1-4中e,A1,A2,B,I,ai为方程参数,进行计算机仿真,得n×m涡卷混沌吸引子的z-y的相图,如图1所示。
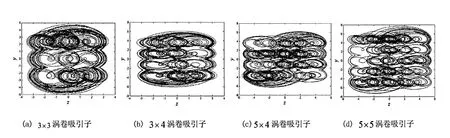
图1 涡卷混沌吸引子
1.2 新系统动力学行为的分析
令式 1﹒x=﹒y=﹒z=0,得到系统的平衡点的方程为 :

对式5方程的平衡点进行分析,得系统的平衡点为P±i,j=(jB-iA,jB,iA),其中,i=0,±1,±2,…,±I,

平衡点Pij对应的Jacobin矩阵为:
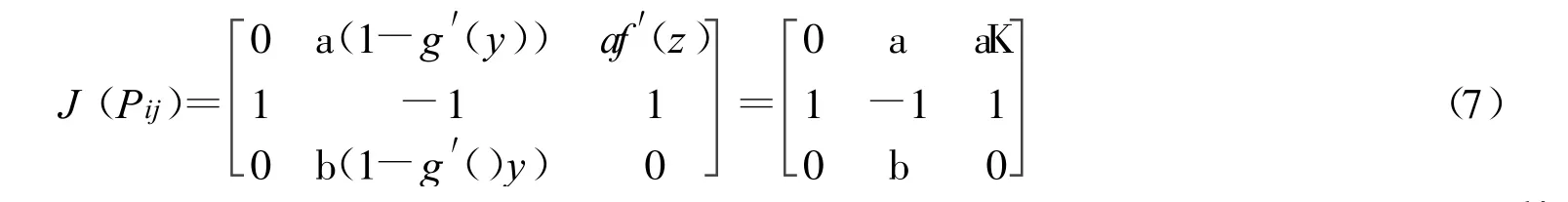
相应的特征方程为-λ3-λ2+(a+b)λ+abK=0,取参数A=1,a=0.125得K+=7,K-=-1。利用上式求得特征值为:

上述分析表明,在式1表示的混沌系统中,存在两种不同类型的鞍点,其中平衡点P+为指标1的鞍点,而平衡点P-则为指标2的鞍点,通过以上分析,满足Shilnikov定理,可在式1系统中形成混沌吸引子。
2 网格多涡卷变形蔡氏电路的分析及设计
根据式1-4,可设计网格多涡卷混沌吸引子的电路如图24所示。以下对电路的设计的基本模块进行说明。
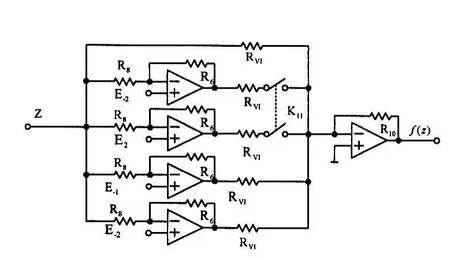
图2 三角波函数序列的电路图

图3 阶跃函数序列的电路图
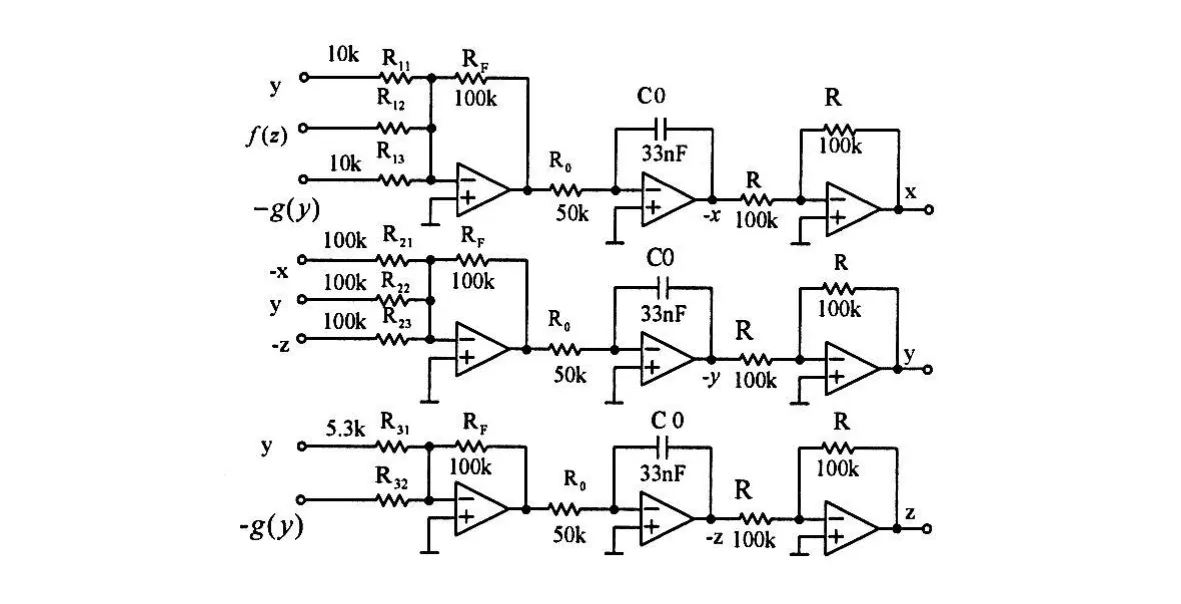
图4 产生网格多涡卷混沌吸引子的电路图
根据式2中的有关参数A和三角波平衡点之间的关系,选取A=1作为一个典型的参数来设计电路,如图2所示。
根据式3、4的有关参数,设计了阶跃函数序列的电路图如图3所示。它由3部分构成:反向比较器、压缩器、反向器。
对式1的状态方程进行电路整体的设计,整个电路由反相加法器、积分器和反相器3大模块构成,电路结构对称。
3 电路实验结果
根据图2~4所示电路进行硬件电路实验,开关状态、比较电压的值和平衡点的电压值如表1所示。硬件实验结果如图5所示,其中图5(a)为3×3涡卷混沌吸引子,图5(b)为3×4涡卷混沌吸引子,图5(c)为5×4涡卷混沌吸引子,图5(d)为5×4涡卷混沌吸引子。

表1 开关状态、比较电压、平衡点的电压与涡卷数量的对应关系
4 结束语
在蔡式电路的基础上,提出了一种用三角波函数序列和阶梯波函数序列产生网格多涡卷变形蔡式混沌吸引子的一种电路设计与实现新方法。计算机数值模拟和电路实验结果,证实了这一方案的可行性。为研究变形蔡氏电路提供的一种新的思想方法,同时也为混沌现象的研究和混沌保密通信提供了基础。

图5 涡卷混沌吸引子
[1]Chua L O etal.The double scroll family[J].IEEE Trans Circuits Syst,1986,33(11):1 073-1 118.
[2]Keneedy M P.Three steps to chaos-PartⅡ:A Chua's circuit primer[J].IEEE Trans Circuits Syst.(part-Ⅰ),1993,40(10):657-674.
[3]Tang W K S,Zhong G Q,ChenG,etal.Generation ofN-scroll attractors via sine function[J].IEEETransCircuitsSyst.(part-Ⅰ),2001,48(11):1 369-1 372.
[4]Matsumoto T,Chua L O,Kobayashi K.Hyperchaos:Laboratory experiment and numerical confirmation[J].IEEE Trans Circuits Syst.(part-Ⅰ),1986,33(11):1 143-1 147.
[5]Yin Y Z.Experimental demonstration of chaotic synchronization in the modified Chua's oscillators[J].International Journal Bifurcation Chaos,1997,7(6):1 401-1 410.
[6]Yu S M,Tang W K S,Chen G R.Generation of n×m scroll attractors under a Chua-circuit framework[J].International Journal Bifurcation Chaos,2007,17(11):1-15.
