基于对应分析的新疆农村居民消费情况

2010-09-02张艳玲

昌吉学院学报 2010年4期

关键词：用品居民消费新疆

张艳玲

(昌吉学院数学系新疆昌吉 831100)

基于对应分析的新疆农村居民消费情况

张艳玲

(昌吉学院数学系新疆昌吉 831100)

以新疆农村地区2000年到2008年这8年评价居民消费情况的8项指标为研究对象,用多元统计学的对应分析进行新疆农村居民消费情况比较研究,结果表明:新疆农村居民在家庭设备、用品及服务、居住、医疗保健、交通和通讯方面的消费上升的较快,尤其以交通和通讯方面的消费增长最为明显;而在食品、衣着、文化教育娱乐用品及服务、其他商品和服务方面的消费增长不是很明显,其中文化教育娱乐用品及服务、其他商品和服务方面的消费近乎零增长。

新疆农村居民消费;对应分析;SPSS统计软件

1 引言

人们在自然科学和社会科学的许多研究工作中,常常需要分析处理含有多个变量的数据问题,研究探索多元关系的复杂性,对应分析作为多元统计分析的一个重要内容,其核心思想是高维度空间的向量向低维度空间的投影,从而解释变量间的相关关系及相关程度,有直观、简便、降低计算复杂性的优点。自20世纪70年代传入我国以来,被广泛应用于地质、医学、生物等各个领域。本文通过对应分析探索西部大开发以来新疆农村居民的消费情况。

2 原理介绍与方法步骤

2.1 原理介绍

对应分析是R型因子分析与Q型因子分析的结合,它是利用降维的思想以达到简化数据结构的目的,不过,与因子分析不同的是,它同时对数据表中的行与列进行处理,寻求以低维图形表示数据表中行与列之间的关系。对应分析的一大特点就是可以在一张二维图上同时表示出两类属性变量的各种状态,以直观、简洁的形式描述属性变量各种状态之间的相关关系及不同属性变量之间的相互关系[4]。它通过一个过渡矩阵Z将二者有机结合起来,具体说就是使含有n个样品p个变量的原始资料矩阵X=(xij)n×p变成一个过渡矩阵Z=(zij)n×p,并使R=Z′Z(分析变量之间关系的协方差矩阵)与Q=ZZ′(分析样品之间关系的协方差矩阵)具有相同的非零特征根,它们相应的特征向量之间也有密切的关系。

对协方差矩阵R、Q进行加权主成份分析或因子分析,分别能提取两个最重要的公因子R1、R2和Q1、Q2。由于采用的是一种特殊变换方法,公因子R1与Q1在本质上是相同的,公因子R2与Q2本质上也是相同的,故可用Diml作为R1与Q1的统一标志,Dim2作为R2与Q2的统一标志,于是可将(R1,Q1)和(R2,Q2)两组数据点在由(Dim1,Dim2)组成的同一坐标系中作出因子平面点聚图,即把变量点和样品点同时反映在具有相同坐标轴的因子平面上,以便对变量点和样品点一起考虑进行分类。

2.2 方法步骤

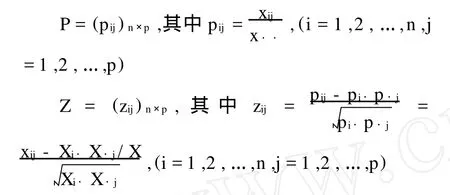
设xij表示第j个指标的第i个样品观测,原始资料矩阵为:

(1)按行、列分别求和,得行和Xi·和列和X·j及总和X··。

(2)由原始矩阵X出发计算数据规格化的概率矩阵P及数据变换矩阵Z。

(4)因子分析

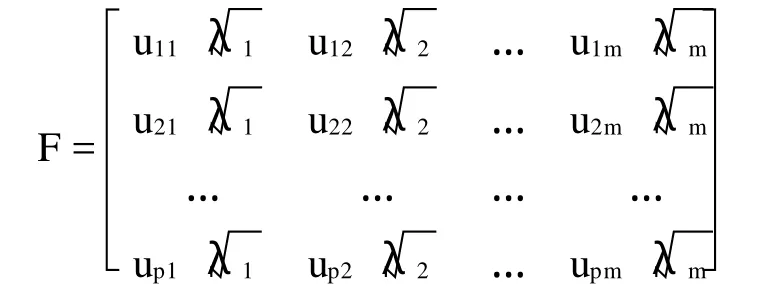
R型计算协方差矩阵R=Z′Z的特征根λ1≥λ2≥…≥λp,一般按累计百分比(贡献率)≥80%取前m个特征根,并计算对应的特征向量u1,u2,…,um,得R型因子载荷矩阵:

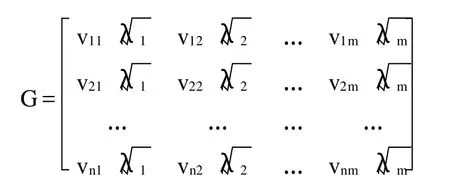
Q型对上述m个特征根λ1≥λ2≥…≥λm,计算对应其矩阵Q=ZZ′的特征向量V1=ZU1, V2=ZU2,…,Vm=ZUm,再将特征向量单位化,得Q型因子载荷矩阵:

(5)在同一坐标轴上作图。由于R和Q具有相同的非零特征根,故相应的因子贡献率相同,R和Q这种对应关系,使得变换后的数据对行和对列是对等的,因而可以对两者对应起来分析。在二维因子轴上作图,将R的第一因子和第二因子及Q的第一因子和第二因子同时绘在同一坐标轴上,即可揭示行因素的不同水平及列因素的不同水平间的对应关系。

3对新疆农村居民消费情况数据的对应分析

根据数据的可得性与科学性,本文选取的是反映新疆农村居民消费情况的8个指标进行考察:食品(X1)、衣着(X2)、居住(X3)、家庭设备、用品及服务(X4)、医疗保健(X5)、交通和通讯(X6)、文化教育娱乐用品及服务(X7)、其他商品和服务(X8)。资料来源于《新疆统计年鉴》(2000年-2009年)。由于目前最新的统计年鉴只能查到2008年的数据,所以本文就研究新疆农村居民过去9年的消费情况。

本文采用SPSS16.0统计软件对九年的数据进行分析[1,2],分析的步骤是首先在新疆农村居民消费8项主要经济指标中找出最能说明主要问题的因子成分,并根据不同权重的最后取值得分利用对应分析的方法进行分析。[3]

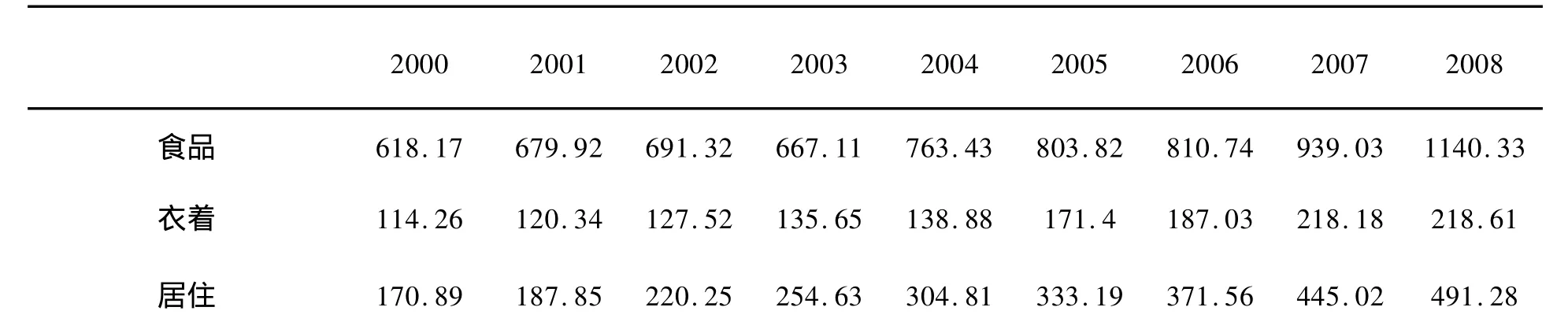
表1 2000年-2008年农村居民消费情况

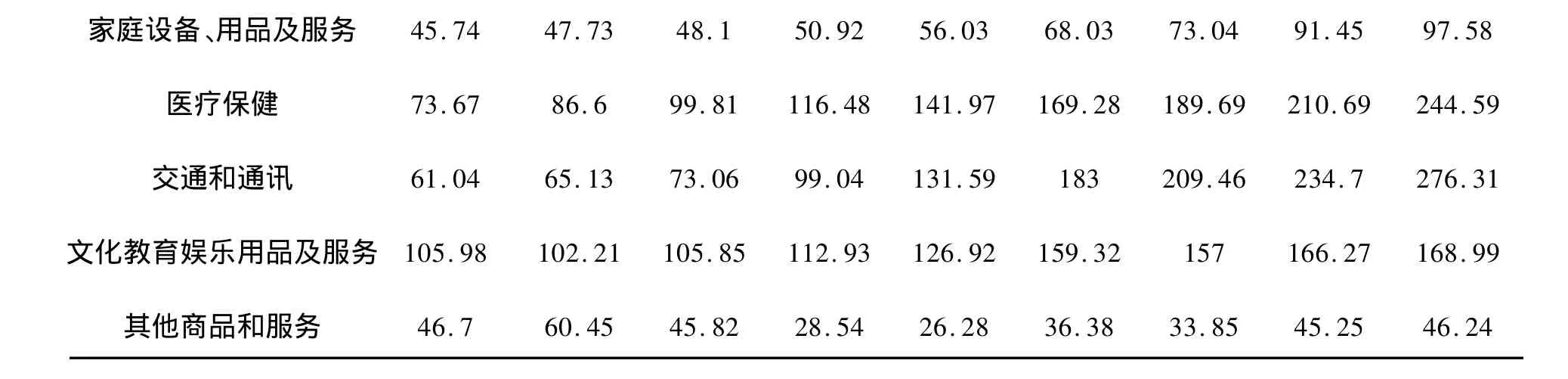
对表1进行对应分析,我们首先得到其惯量和χ2的分解,见下表:

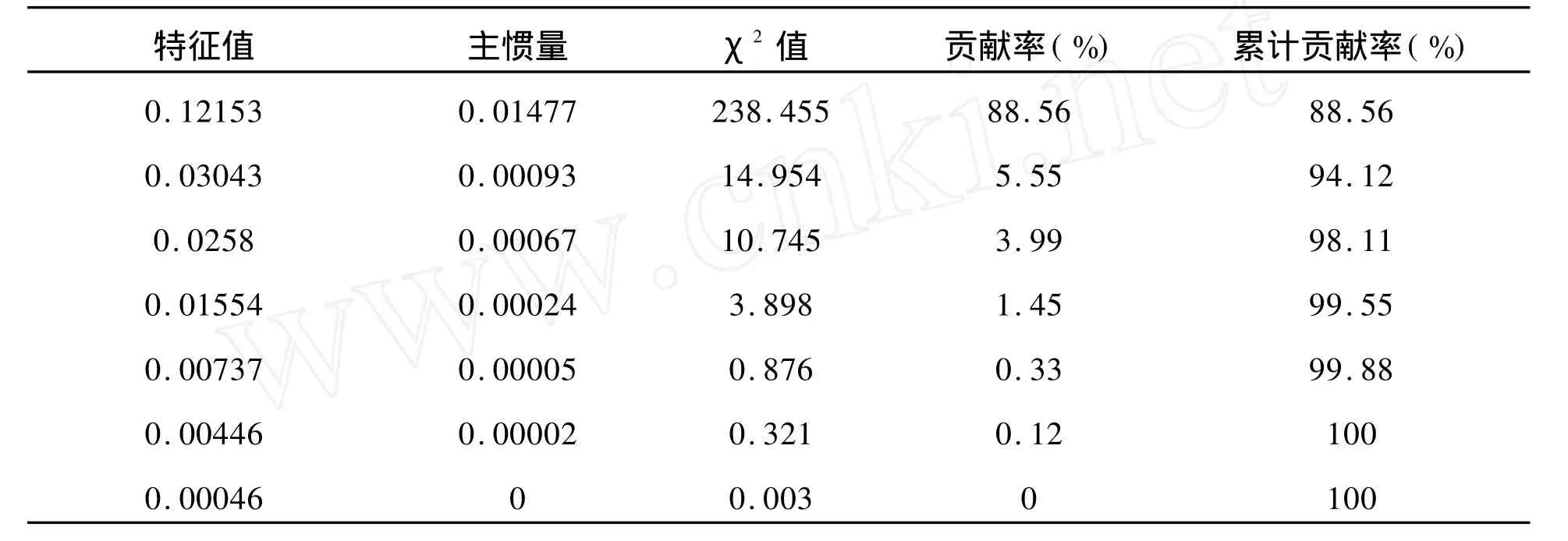
表2 惯量和χ2的分解

由表2可知,前两个公因子的累计贡献率达到94.12%,解释了原列联表资料的大部分信息,因此两个公因子表示的二维因子载荷图可以基本表达消费与年份两属性变量间的关系,且第一个公因子的贡献率已经达到88.56%,以第一维度为主。从而可以得到年份因子和消费因子在这两个公因子上的因子载荷与信息量,见表3和表4:

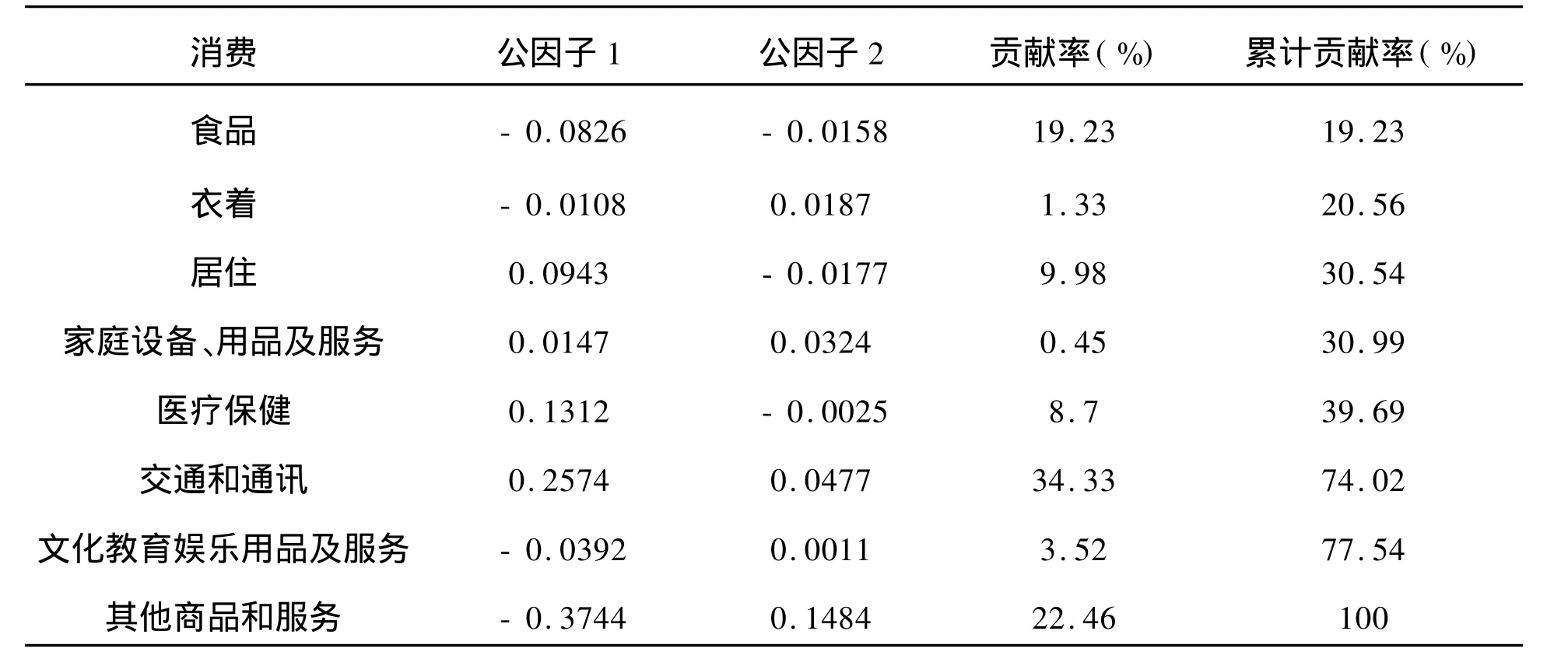
表3 消费因子(行因子)载荷与信息量

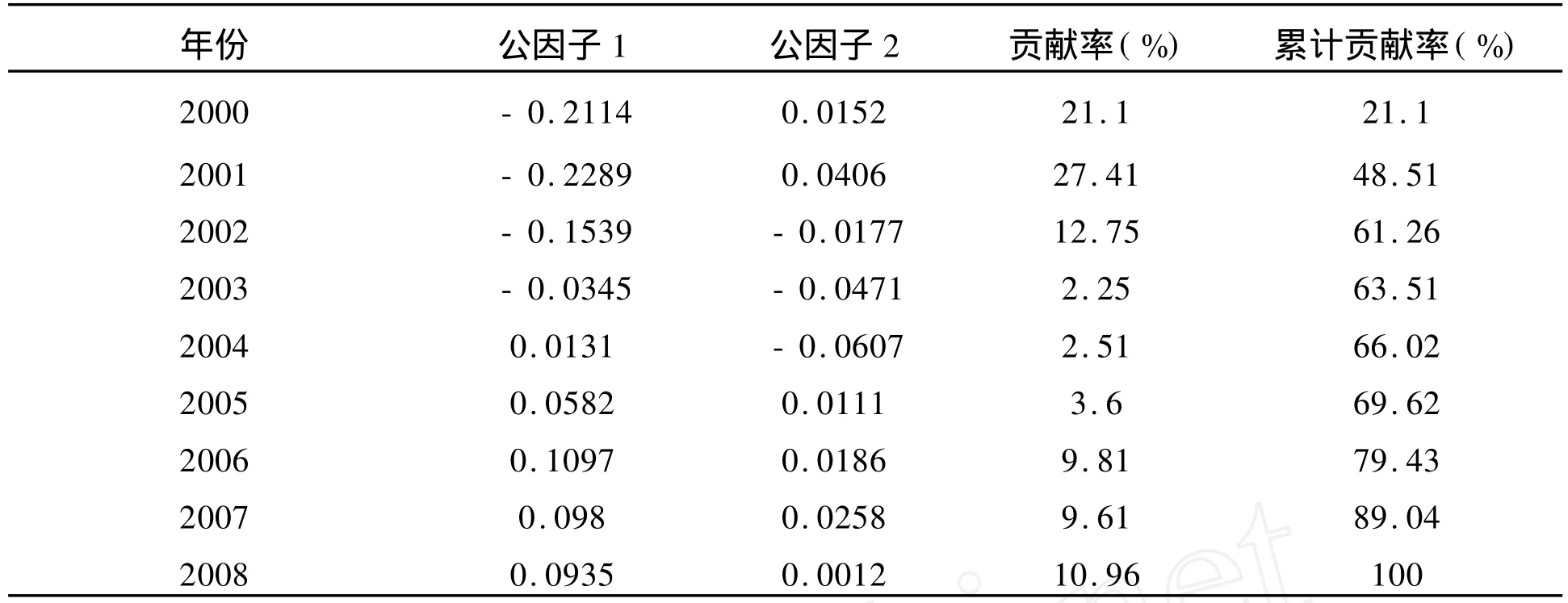
表4 年份因子(列因子)载荷与信息量

由表3可知,近年来,新疆农村居民的消费主要集中在交通和通讯、其他商品和服务、食品上。表3和表4分别显示了消费因子和年份因子在两个公因子上的载荷,以表3中的食品为例,其结果可表示为:食品=-0.0826＊Dim1-0.0158＊Dim2。即在Dim1与Dim2作为纵坐标与横坐标的直角坐标系中,每一种消费就是一个点,如食品的坐标为(-0.0826,-0.0158)。且消费与年份的平面聚合图如下图所示:

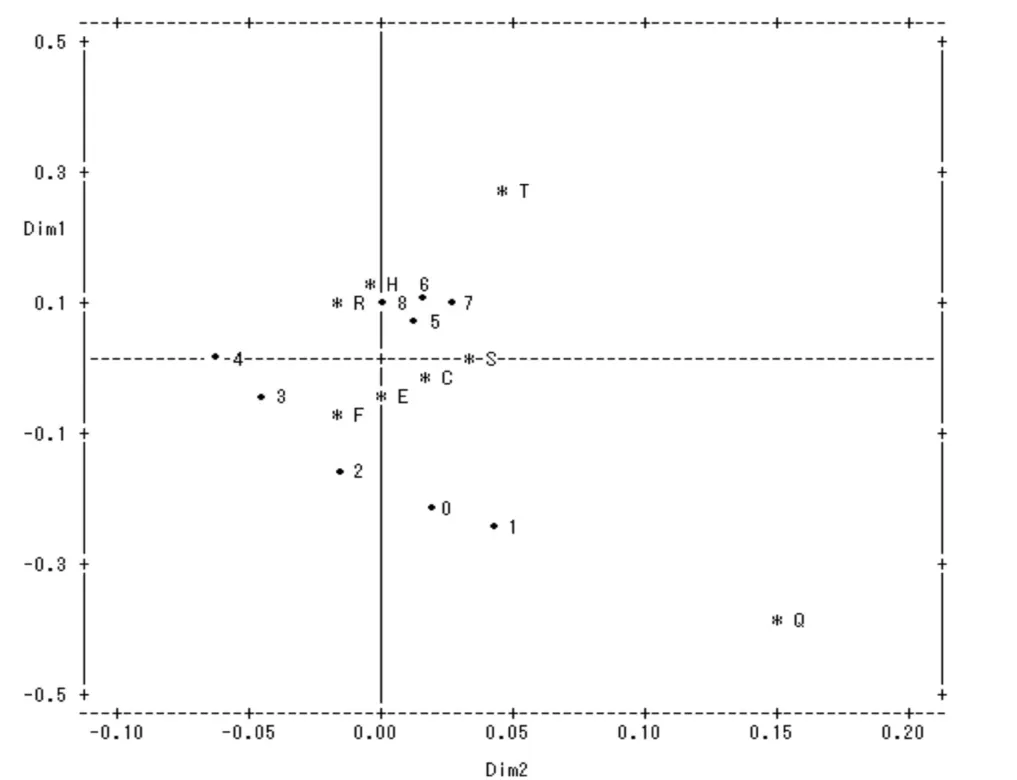
图1 消费与年份的平面聚合图

在Dim1＊Dim2的图表中,表示年的这些点用年数减去2000得到的单个数字标图,表示消费指标的这些点按表1中的顺序依次表示为F、C、R、S、H、T、E、Q。由图1可以看出,从2000年到2008年,新疆农村居民在家庭设备、用品及服务、居住、医疗保健、交通和通讯方面的消费上升的较快,尤其以交通和通讯方面的消费增长最为明显;而在食品、衣着、文化教育娱乐用品及服务、其他商品和服务方面的消费增长不是很明显,其中文化教育娱乐用品及服务、其他商品和服务方面的消费近乎零增长。