空间三平面的相关位置

李 燕 陈香莲

(1,2.昌吉学院数学系 新疆 昌吉 831100)

空间三平面的相关位置

李 燕1陈香莲2

(1,2.昌吉学院数学系 新疆 昌吉 831100)

本文归纳了空间三个平面的相关位置共有五种类型,并且进一步给出其各种位置关系的判定方法。

空间直线;相关位置;向量;充要条件

1 引言

在解析几何教学中,两平面相关位置的类型及其判定是一项重要内容,文献[1]详细介绍了空间两平面的三种相关位置关系的判定条件。作为教材,文献[1]为读者继续探讨空间三个平面相关位置提供了理论基础和思索空间。

在空间,两个平面的相关位置有三种情形[1]:即相交、平行和重合,并且每种情形一般是通过在直角坐标系下,各平面的法向量的关系来进行判定的。现在约定,若两平面重合,就将二者合二为一,视作同一平面。接下来,在直角坐标系下我们就空间三个平面的相关问题进行研究。

2 空间三平面相关位置的类型

我们从探讨三个平面中两两平面相互位置关系出发,结合方程组解的情况和向量分析,讨论空间中三个平面的相互位置关系。

设有三个互不重合的平面π1,π2,π3,它们的方程为:

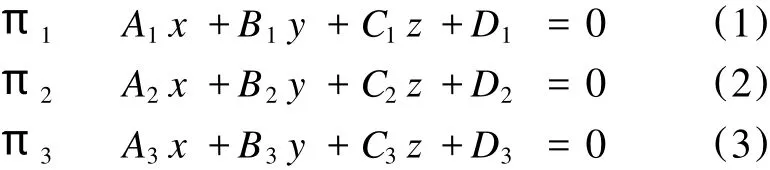
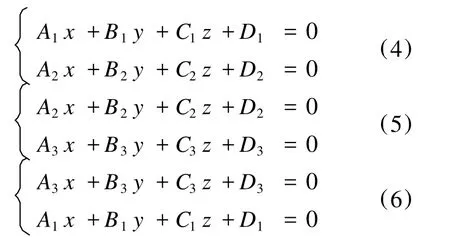
同时考虑(4)(5)(6)这三个方程组,会有四种情形,分别如下:

(ⅰ)全部都无解,即l1,l2和l3都不存在,即三个平面两两平行。

(ⅱ)有且只有一个方程组有无数组解,其余方程组都无解,而这种情况是不可能存在的,因为不妨假设l1存在,则l2与l3都不存在,那么π1与π3平行,π2与π3平行,从而π1与π2平行,这与l1存在相矛盾,从而得证。

(ⅲ)有且只有一个方程组无解,其余方程组都有无数解,即有一个平面与其余两平行平面相交。

(ⅳ)全部都有无数解,即三平面两两相交,对于这种情形,我们需做进一步的分析。

在l1,l2和l3中,任何两条直线都是共面的,则它们有三种位置关系[3]:重合、平行和相交,如果l1与l2重合,那么l3与l1和l2都重合,即三平面过同一直线;如果l1与l2平行,那么l3与l1和l2都平行;如果l1与l2相交于一点,那么l3分别与l1和l2也都相交这一点,从而在三平面两两相交的情况下,又具体存在三种相互位置关系。

综上所述,空间三平面相关位置共有五种类型。

3 空间三平面相关位置的判定方法

为l1上任意一点).

4 应用举例

下面通过一个具体的算例,来说明上述判定方法在三平面相关位置研究中的应用。

5 小结

我们在两平面相关位置的类型及其判定的理论基础上,结合代数方法,阐述了空间三个平面的相关位置类型,并且给出判定方法,最后通过实例说明了该判定方法的具体过程及其有效性。利用这些结论我们除了能解决空间三平面的相关位置以及相应的计算,还可以在其它方面有所应用,比如关于三平面划分空间的几何问题,并且为更多个平面的相关位置的判定提供一些方法和思想。

[1][5]吕林根等编.解析几何(第四版)[M].北京:高等教育出版社,2006:110-111.

[2]郝秉新等编.高等代数(第四版)[M].北京:高等教育出版社,2006.

[3]同济大学应用数学系编.高等数学(第六版)[M].北京:高等教育出版社,2007.

[4]石留杰,李艳军.关于平面束一般方程的应用[J].高校理科研究,2008:72-73.

(责任编辑:马海燕)

O182.2

A

1671-6469(2010)05-0099-03

2010-09-05

昌吉学院研究生科研启动基金项目(09SSQD019)

李燕(1977-),女,安徽省涡阳县人,昌吉学院数学系,讲师,研究方向:基础数学及偏微分方程数值解法。