基于可靠度敏感性的神经网络法研究边坡稳定性
2010-08-29吴坤铭王建国谭晓慧冯敏杰
吴坤铭,王建国,谭晓慧,冯敏杰
(1.合肥工业大学土木与水利工程学院,安徽合肥 230009;
2.合肥工业大学资源与环境工程学院,安徽合肥 230009;3.皖西学院建筑与土木工程学院,安徽六安 237012)
基于可靠度敏感性的神经网络法研究边坡稳定性
吴坤铭1,3,王建国1,谭晓慧2,冯敏杰2
(1.合肥工业大学土木与水利工程学院,安徽合肥 230009;
2.合肥工业大学资源与环境工程学院,安徽合肥 230009;3.皖西学院建筑与土木工程学院,安徽六安 237012)
针对边坡工程结构功能函数不能显式表达的可靠性分析问题和非线性问题计算量大的弊端,研究结构可靠度敏感性,提出参数的相对敏感性分析方法,并基于该方法提出了神经网络法分析边坡稳定性。具体思路:由可靠指标对随机变量分布参数的相对敏感性分析,确定边坡可靠度主要影响参数;用神经网络模型近似替代响应量与基本变量间的隐式极限状态函数,根据蒙特卡罗模拟法,对网络模型进行可靠度分析,求解结构可靠度指标。基于可靠度敏感性的神经网络法,对均值和成层边坡进行稳定性分析,与传统可靠度计算方法相比,结果表明:该方法分析边坡稳定性是准确的且具有较高的计算效率。
可靠度;敏感性分析;神经网络;蒙特卡罗模拟法
滑坡是水利、水电、公路、建筑等各工程领域中最为常见和重要的地质灾害,每年给人民生命财产带来巨大损失。因此,对边坡稳定性进行科学的评价极为重要。本文针对边坡工程中的非线性功能函数及非线性计算量大的问题,研究边坡可靠度敏感性,提出参数的相对敏感性分析方法,并基于可靠度敏感性分析提出神经网络法分析边坡稳定性。
1 结构可靠度敏感性分析
1.1 可靠指标对随机变量分布参数的敏感性分析
设基本随机变量为 X=(X1,X2,…,Xn),极限状态方程为 g(X)=0,将 X转化为相互独立的标准正态随机变量Y,功能函数 g(X)相应地成为 G(Y)。将G(Y)在验算点Y*处展开,有
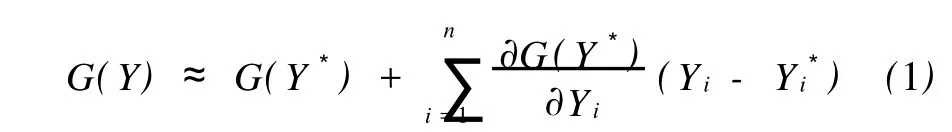
根据可靠指标的定义,β为原点到验算点 Y*的距离,于是可得

已知标准正态空间,可靠指标对随机变量的分布参数bj(j=1,2,…,m)的敏感性表示为[1]:
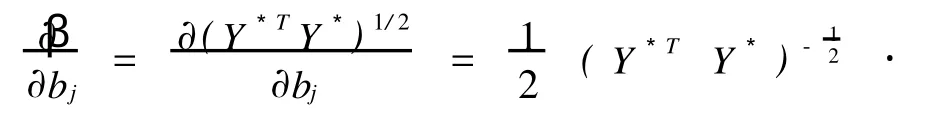

标准正态空间随机变量 Y与原始空间基本变量X满足以下关系:

其中,T是随机变量转换矩阵;B为补充转换向量。
为计算功能函数梯度 ▽G(Y*),设 X变换为 Y的J acobian矩阵为JXY,令 JXY=(σXA)T、X=σXA Y +μx,则 Y、▽G(Y*)分别为:

其中,μX=(μX1,μX2,…,μXn)T为随机向量X的平均值;σX=diag(σX1,σX2,…,σXn)为随机向量 X的均方差;A是下三角矩阵。
由式(6)可得


1.2 可靠指标对极限状态方程参数的敏感性分析
由文献[1,2]知,在Y空间中

其中,CX=σXρXσX为随机向量 X的协方差矩阵。
比较式(4)、式(5)可得
1.3 可靠指标对随机变量分布参数的相对敏感性分析
比较式(10)、(16),可知:∂β/∂μX=∂β/∂X,即在随机变量的原始空间中,可靠指标对参数均值的敏感性与可靠指标对极限状态方程参数的敏感性本质相同。
但是,由于随机变量 Xi的单位各不相同,因此式(10)、(16)并不能反映各参数对可靠指标敏感性的相对大小。所以,本文提出用(∂β/∂μXi)·σXi及(∂β/∂σXi)·σXi进行参数的相对敏感性分析,由式(10)、(11)可得:
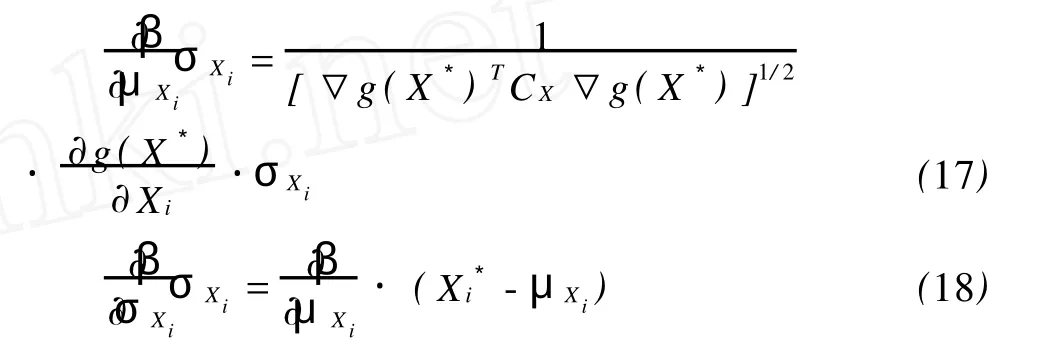
以下通过算例,验证本文提出的可靠指标对随机变量分布参数的相对敏感性分析,并确定边坡可靠度主要影响参数。
1.4 算例分析
有一坡比为1:1的均值土坡[3](P52-95),坡高 H= 2m,粘聚力c=40K Pa,内摩擦角φ=20°,膨胀角Ψ =20°,容重γ=20KN/m3,弹性模量 E=20M Pa,泊松比μ=0.3。
为分析各参数对计算结果的影响,参照文献[4]中有关土工参数的变异系数资料,假设参数c,φ,Ψ, γ,E,μ的变异系数δX=(0.3,0.3,0.3,0.03,0.3,0. 3)T,各参数互为独立,计算结果如表1所示。
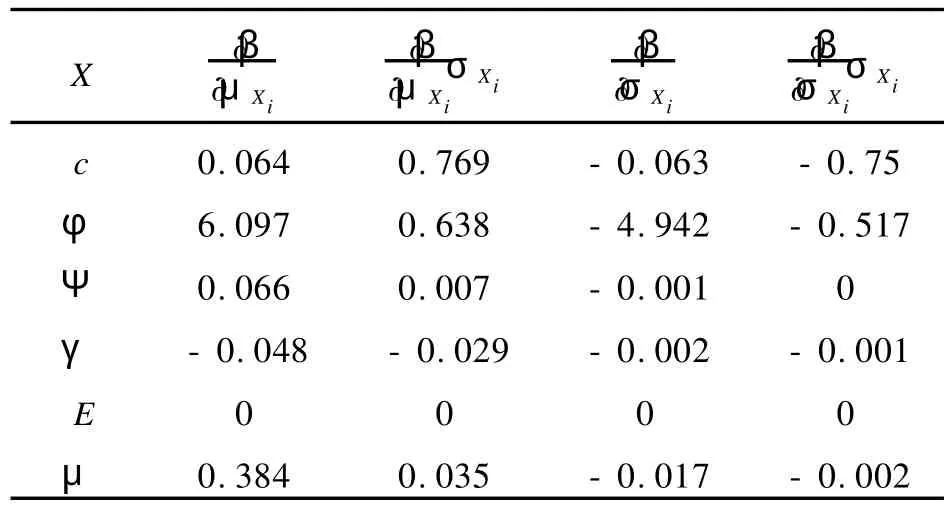
表1 可靠指标对参数的敏感性分析
表1计算结果表明:由于各参数单位不同,∂β/∂μXi、∂β/∂σXi的值对各参数变化较大,缺乏可比性;相对敏感性指标(∂β/∂μXi)·σXi、(∂β/∂σXi)·σXi则消除了参数单位的影响,能较好地反映各参数对可靠指标的相对影响大小。由表中(∂β/∂μXi)·σXi、(∂β/∂σXi)· σXi值,表明参数c,φ对可靠指标的影响最大,其余四个参数对可靠指标的影响很小,因此可以视Ψ,γ,E,μ四个参数为常数,这将大大减少计算的工作量。
进一步分析仅视参数c,φ变异性与视所有参数变异性对可靠指标计算结果的影响,假设δX分别为: δX=(0.3,0.3,0,0,0,0)T、δX=(0.3,0.3,0.3,0.03, 0.3,0.3)T,计算结果如表2所示。

表2 不同基本变量的可靠指标
由表2可知:可靠指标的计算结果印证了本文的敏感性分析,即:视边坡所有参数为基本变量与仅考虑参数c,φ为基本变量时的可靠指标基本一致,也即参数c,φ对可靠指标的影响最大而其他参数的影响可以忽略不计。
2 基于可靠度敏感性的神经网络法分析边坡稳定性
2.1 基于可靠度敏感性分析确定边坡参数
由第1节结构可靠度敏感性分析可知:参数c,φ对可靠度指标的影响最大而其他参数的影响可以忽略不计。因此对于边坡,通过不同的样本取样法选择多组边坡的参数:粘聚力ci、内摩擦角φi(下标i,表示第i组参数)、容重γ保持不变;由此构造神经网络模型学习样本及检验样本所需参数。
2.2 神经网络法可靠度分析基本原理
本文以神经网络法对边坡可靠度进行分析,以B P神经网络-蒙特卡罗模拟法(A N N-MCSM法)为基础。具体方法:通过尽可能少的一系列数值计算建立网络模型(B P神经网络模型);由网络模型近似替代响应量与基本变量间的隐式极限状态函数;根据蒙特卡罗模拟法[5](P155-160)[6](P64-68),对网络模型进行可靠度分析,求解结构可靠度指标。
2.3 神经网络的蒙特卡罗模拟法计算步骤
(1)构造学习样本及检验样本;
2.2有利于培养“双师型”教师 教师从事临床护理工作,为学校护理教育与临床护理实践无缝对接提供了基础,也是评价高职院校护理教学质量的标准之一。对于教师自身来说教学实践和临床实践的结合,不仅使自己具备“双师”素质,更为成为专家型、创新型的教学名师探索路径[5]。
按式(19)定义功能函数,安全系数 K为随机变量的函数;用Morgenstren-Price求解各组参数ci、φi对应的安全系数 Ki;以各组参数及对应的安全系数Ki作为边坡稳定可靠度分析的训练样本;对于不同的算例采用随机取样法或中心复合取样法构造各自的学习样本和检验样本。(2)训练网络,形成响应面函数;

(3)利用蒙特卡罗模拟法对求得的响应面函数进行可靠度分析。
2.4 算例
算例1:如图 1所示一均质边坡[7],容重γ为 20kN/m3,粘聚力及内摩擦角是互为独立的正态变量,其均值分别为:μc=10k Pa,μφ=30°,变异系数δX1=δX2的变化范围是0.1~0.3。

图1 边坡剖面图
算例2:如图2所示边坡由两层材料组成,土层的容重为定值,γ1=γ2=20kN/m3。粘聚力及内摩擦角是互为独立的正态随机变量,其均值分别为:μc1= 10k Pa,μc2=12k Pa,μφ1=15°,μφ2=14°,变异系数δX1=δX2=δX3=δX4的变化范围为0.1~0.3。
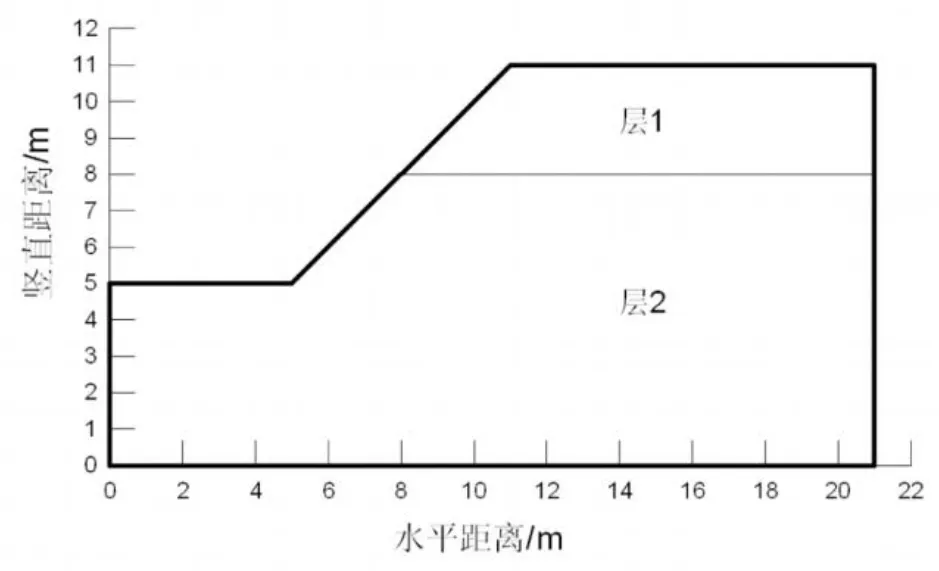
图2 边坡剖面图
分别采用定值法及可靠度分析法对算例1及算例2进行边坡稳定性分析。
定值分析采用 Morgenstern-Price求解安全系数,得算例1边坡安全系数 K1=1.481,算例2边坡安全系数 K2=1.052。
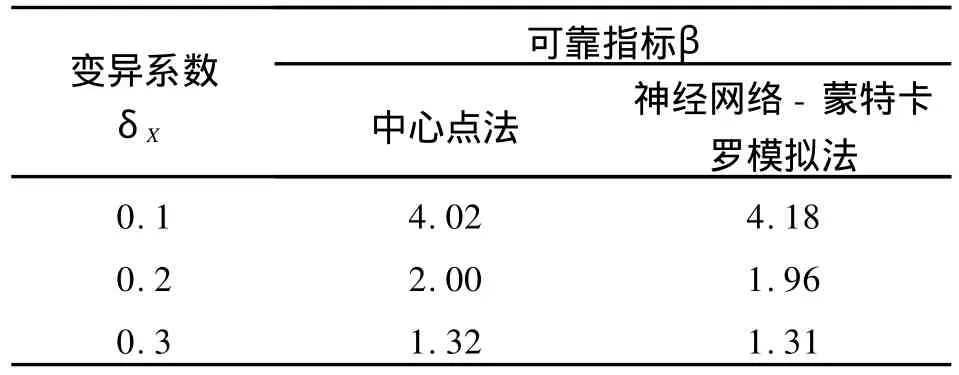
表3 可靠指标-变异系数变化表
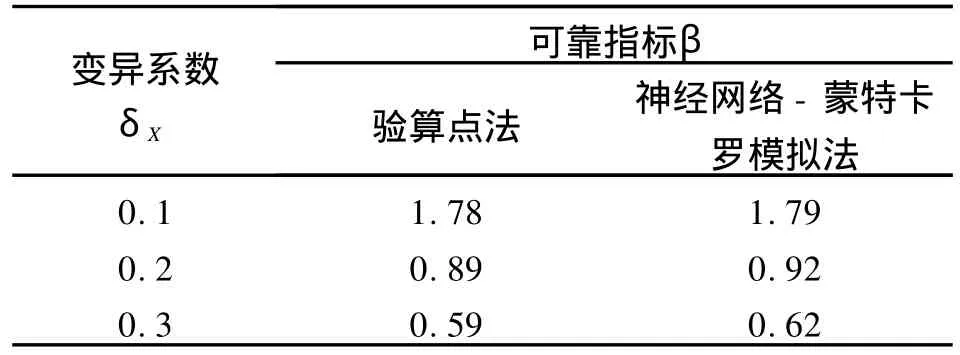
表4 可靠指标-变异系数变化表
通过对算例1、算例2的可靠性分析,由表3、表4可靠指标β随变异系数δX的计算结果可知:
(1)在变异系数δX取值相同的情况下,基于神经网络的蒙特卡罗模拟法和传统可靠度方法的可靠指标β计算结果相近,说明:采用神经网络的蒙特卡罗模拟法,对边坡进行可靠度分析,其结果是准确的。
(2)当变异系数δX在0.1~0.3之间变化,定值法分析时,安全系数(K1=1.481;K2=1.052)恒为大于1的常数即安全的;可靠度分析时,可靠度指标β随变异系数δX增大而减小,且β变化幅度较大;算例2由定值分析是安全的而可靠度分析时为失稳;因此,由定值分析和可靠度分析可知算例1安全、算例2失稳。
(3)由算例1、算例2程序运算过程可知,传统可靠度计算方法耗时较长,而神经网络法耗时较短,因此神经网络法计算效率远高于传统可靠度计算方法。
3 结论
(1)本文针对边坡工程中的非线性功能函数及非线性计算量大的问题,研究边坡可靠度的敏感性,提出参数的相对敏感性分析方法。
(2)对于边坡问题,通过算例,由可靠指标对随机变量分布参数的相对敏感性分析可知:参数c,φ对可靠指标的影响最大;其余参数可视为常数,这将大大减少计算的工作量。
(3)针对边坡问题,提出了神经网络法,由网络模型近似替代响应量与基本变量间的隐式极限状态函数,根据蒙特卡罗模拟法,对网络模型进行可靠度分析,求解结构可靠度指标。
(4)通过算例,采用基于可靠度敏感性的神经网络法,对均值和成层边坡进行可靠性分析。与传统可靠度计算方法相比,结果表明:该方法分析边坡稳定性是准确的且具有较高的计算效率。
[1]Imai K,Frangopol D M.Geometrically Nonlinear Finite Element Reliability Analysis of Structural Systems.I:Theory [J].Computers and Structures,2000,77(6):677-691.
[2]迟世春,关立军.基于强度折减的拉格朗日差分方法分析土坡稳定性[J].岩土工程学报,2004,26(3):42-46.
[3]朱小林.土体工程[M].上海:同济大学出版社,1998.
[4]高大钊.土的抗剪强度指标的统计方法[J].工程勘察, 1986,(4):1-5.
[5]贡金鑫.工程结构可靠度分析方法[M].大连:大连理工大学出版社,2003.
[6]杨伟军,赵传智.土工工程结构可靠度理论与设[M].北京:人民交通出版社,1999.
[7]Y.M.Cheng,T.Lansivaara,W.B.Wei.Two-dimensional Slope Stability Analysis by Limit Equilibrium and Strength Reduction Methods[J].Computer and Geotechnics,2007, 34(3):137-150.
Research on Slope Stability Based on Neural Networks Method of Reliability Sensitivity
WU Kun-ming1,3,WAN GJian-guo1,TAN Xiao-hui2,Feng Min-jie2
(1.School of Civil Engineering,Hef ei University ofTechnology,Hef ei230009,China;
2.School of Resources and Environment Engineering,Hef ei University of Technology,Hef ei230009,China;
3.College of A rchitecture and Civil Engineering,West A nhui University,L u’an237012,China)
A reliability analysis of slope stability using neural networks method is presented in this paper,which based on relative sensitivity analysis of the structural reliability.It is especially useful in such reliability analysis problems as slope stability whose performance functions are implicit and nonlinear problems have large amount of calculations.Specific ideas:To access the reliability of the main effects of slope parameters based on reliable indicator of the random variable distribution parameters of the relative sensitivity,with neural networks models approximate amount of alternative responses and basic variables of the implicit limit state functions,to analyze the reliability of network model and to solve structural reliability index based on the Monte Carlo simulation. Research on slope stability based on neural networks method of reliability sensitivity and compared with traditional reliability calculation methods,the results show that:the method of slope stability analysis is accurate and has higher efficiency.
reliability;sensitivity analysis;neural networks model;Monte Carlo simulation
TP183
A
1009-9735(2010)05-0102-04
2010-09-10
国家自然科学基金项目(40972194);安徽高校省级自然科学研究项目(KJ2010B267)。
吴坤铭(1978-),男,安徽六安人,皖西学院建筑与土木工程学院讲师,合肥工业大学在读博士生,研究方向:岩土力学。
