双馈风电机组线性建模及特性分析*

肖运启

(华北电力大学控制与计算机工程学院，北京 102206)

0 引言

基于双馈电机的交流励磁变速恒频(VSCF)风力发电系统，实现了机电系统的柔性连接，可以使风力机运行范围达到同步速的70%～130%，更加满足低风速下风力机追踪最大风能的控制需求，发电效率更高。因此，其逐渐成为风力发电的主流形式。

双馈发电机利用双向变频器对转子绕组以转差频率进行交流励磁，进而满足定子侧频率要求。其励磁系统控制通常采用矢量控制技术对定子电流的转矩分量和励磁分量进行解耦，实现有功、无功输出的独立调节［1-3］。但两分量之间还存在着与发电机转差率相关的耦合作用，导致在不同转速下发电机表现出不同的动态特性，且受参数检测速度和精度的影响。实际运行中耦合难以完全补偿，给变速运行中控制效果的保持增加了难度。

本文对双馈发电机变速恒频运行中动态特性变化规律进行分析。以同步旋转坐标下双馈发电机系统非线性数学模型为基础，应用小扰动分析方法，建立机组对象的线性模型。通过对不同运行工况下模型极点分布情况的分析，总结出双馈发电系统动态特性变化规律，为双馈发电机控制系统设计及控制器参数整定提供参考依据。

1 双馈型风力发电系统

1.1 系统结构

双馈型风力发电系统结构如图1所示，风力机通过变速齿轮箱与双馈发电机相连。发电机定子绕组直接接入工频电网，转子绕组接线端由三只滑环引出，通常由一台双向变频器接至电网，可以对转子进行交流励磁，其转子绕组励磁电流频率满足:

式中:f1——电网频率;

f2——转子励磁电流频率;

fm——转子旋转频率;

np——电机极对数。

因此，双馈发电机定子感生电压始终满足电网频率，从而保证系统变速恒频运行。

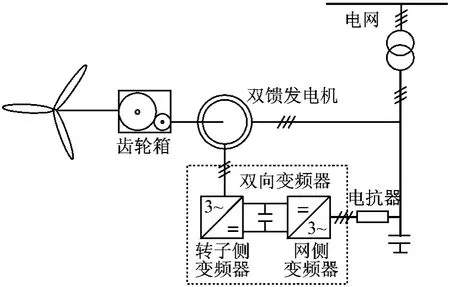
图1 双馈风电机系统结构

1.2 系统数学模型

为便于分析双馈发电机特性，通常在dq同步旋转坐标系下建立数学模型，将d轴与双馈电机定子磁链Ψs重合，如图2所示。

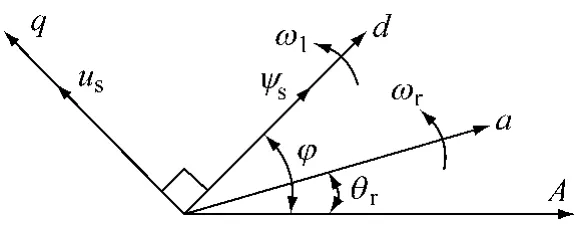
图2 矢量坐标变换系统

定子侧取发电机惯例，转子侧取电动机惯例，可得发电机系统方程［1-3］为

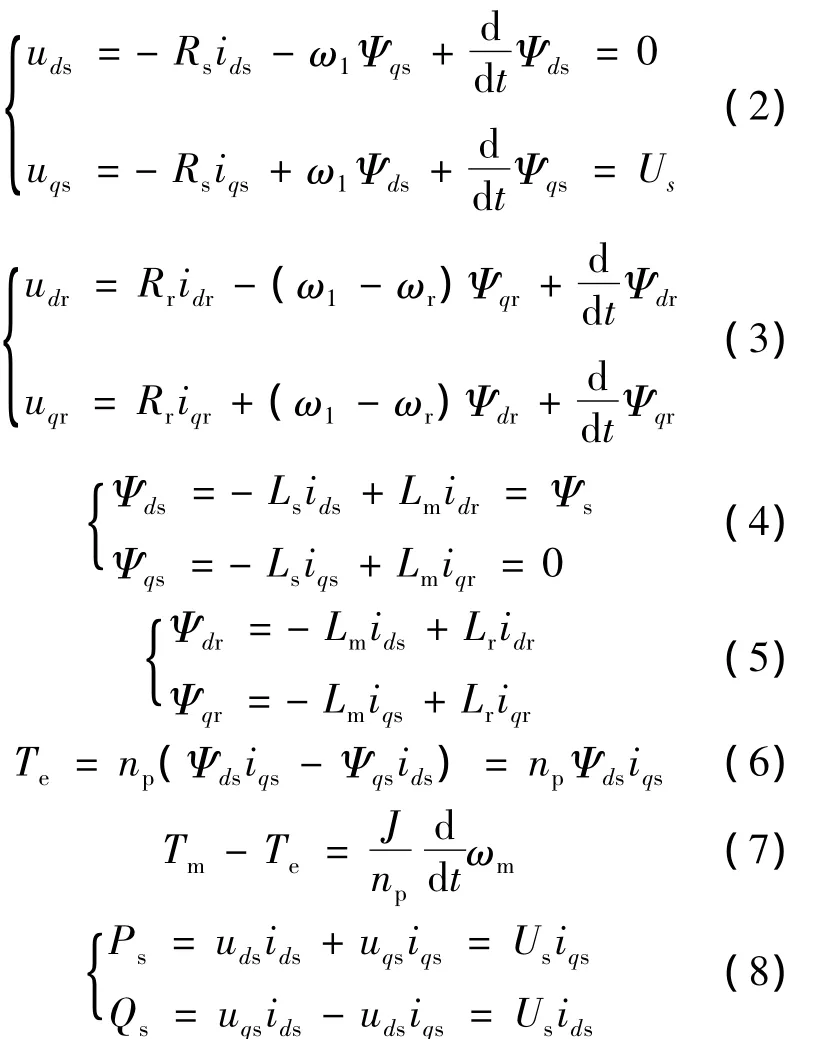
式中:uds、uqs，udr、uqr——定、转子d、q轴电压;

Us——电网电压矢量幅值;

ids、iqs，idr、iqr——定、转子d、q轴电流;

Ψds、Ψqs，Ψdr、Ψqr——定、转子d、q轴磁链;

Ψs——定子磁链矢量幅值;

ω1——同步角速度;

ωr——转子电磁角速度;

Rs，Rr——定、转子等效电阻;

Ls、Lr，Lm——定、转子等效自感和互感;

Te，Tm——电磁力矩和机械力矩;

J——轴系统转动惯量;

np——电机极对数;

ωm——转子转速，ωm=ωr/np。

忽略定子电阻压降，将式(2)、(4)、(5)整理代入式(3)得:

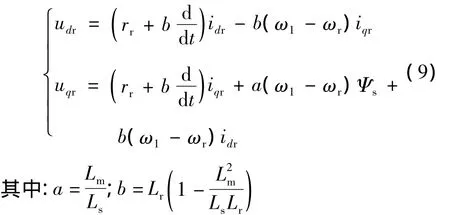
据此可以得到dq同步旋转坐标系下双馈发电机对象模型框图，如图3所示。

2 双馈发电机线性化模型

从图3可以看出，双馈发电机转矩分量(uqr支路)与励磁分量(udr支路)间具有耦合关系，而且随着发电机的大范围变速运行，转差率ωs会随之变化，耦合量bωs的值也随之变化，使发电机对象表现出非线性，从而影响控制效果。因此，深入研究变速运行下发电机对象动态特性变化规律十分必要，这就需要首先建立双馈发电机对象的线性模型。在电力系统分析中，小扰动分析法是一种常用的、有效的线性化建摸方法，本文即采用该方法建立双馈发电机对象的线性模型，为后续的特性分析提供基础。

2.1 模型的线性化

对于双馈发电机系统，通常最主要的扰动来自风速波动引起的发电机输入转矩变化，以及由变频器控制系统调节引起的d、q轴电压变化。因此，在线性模型中以负载转矩、转子控制电压的小扰动量为输入，以转差率、转子电流的小扰动量为状态变量，来分析其对发电机功率、转速等重要系统输出量的影响。

将基于定子磁链定向的同步旋转坐标系下双馈发电机模型利用小扰动分析法展开，式中变量加前缀‘Δ’表示小扰动量，加角标‘0’表示稳态量。

将式(9)按稳态量和小扰动量分解展开:

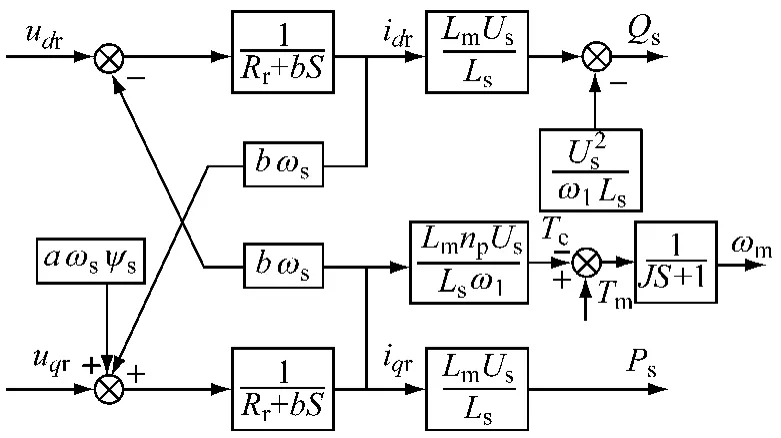
图3 dq坐标系下双馈发电机模型框图

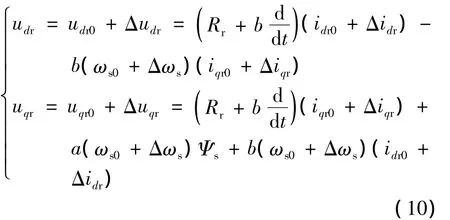
将式(10)分离小扰动量，得到电流小扰动量微分状态方程:

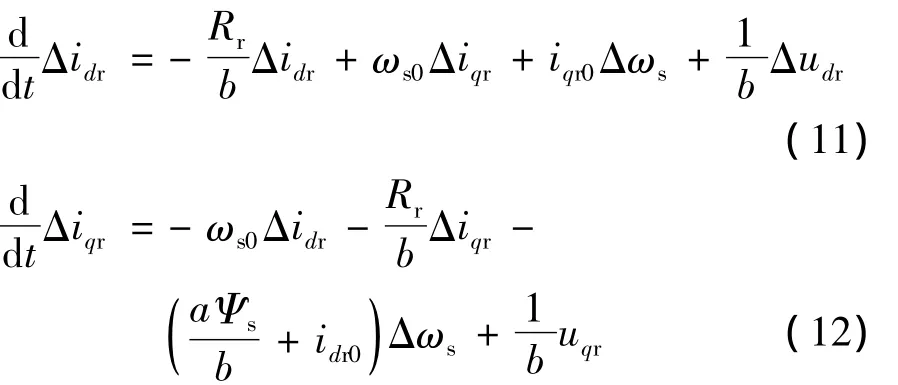
同理，将式(7)电磁力矩方程展开:

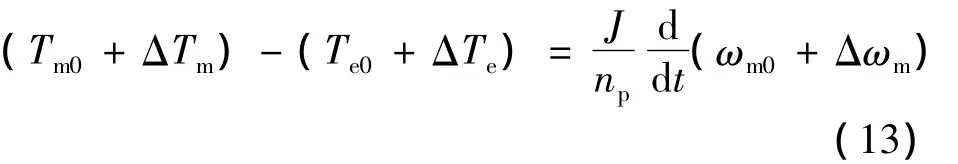
ms速小扰动量微分状态方程:

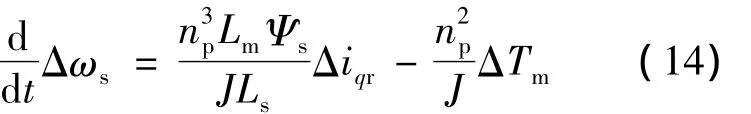
双馈发电机定子功率是主要的运行参数，对式(8)也应用小扰动分析法:得到输出功率的小扰动量方程:

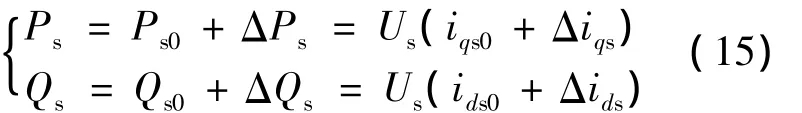
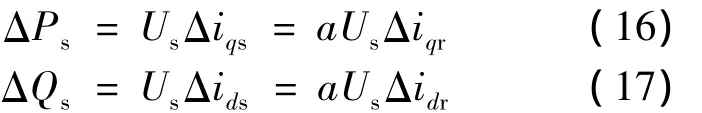
2.2 小扰动信号模型

在确定的工况点上，小扰动信号方程中的稳态量可认为是常数。所以由式(11)、(12)、(14)得到的是常系数微分方程，可建立小扰动信号的状态方程:

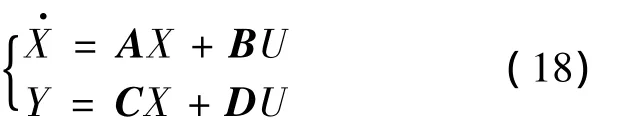
式中:状态变量X=［ΔidrΔiqrΔωs］T;输入量U=［ΔudrΔuqrΔTm］T;输出量Y=［ΔQsΔPs

ΔTeΔωm］T。系数矩阵 A、B、C、D 分别为

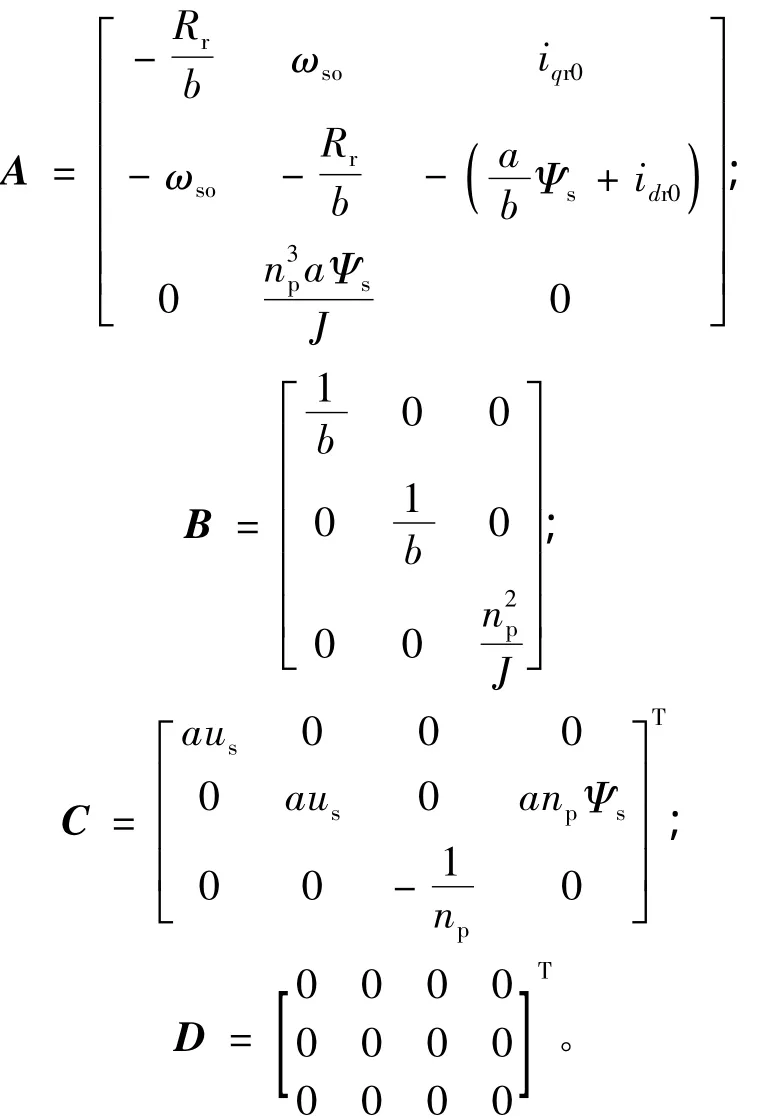
传递函数矩阵G(s):

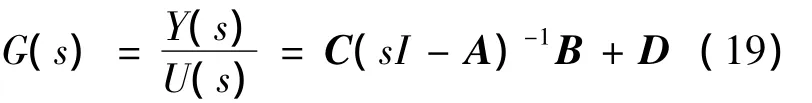
可见，在矩阵A、B、C中，只有转差速度ωs0直接与机组转速相关，不同转速下运行的双馈风电机组的线性模型不同，其动态特性必然存在一定差异。

3 动态特性分析

目前，双馈风电机组容量从kW到MW级，范围很广，动态特性需要具体机组具体分析。但是，由于各种容量的双馈电机的工作原理基本相同，电磁方程也一致，所以建立的线性模型传递函数G(s)具有适用性。G(s)中只有转差速度ωs0与机组工况点有关，受励磁变频器变频范围和电机机械性能的约束，通常情况下转差速度ωs0都为其同步转速的70% ～130%。因此，即使是不同容量的双馈风电机组，变速运行下动态特性的变化规律具有一定的相似性。本文以某具体型号双馈发电机为研究对象得出的结论具有适用性。分析用机组参数如下:风轮半径为2.4 m;桨叶目数为3;齿轮箱增速比为1∶7.846;轴系转动惯量为0.89 kg/m2;最佳叶尖速比为9.5;最大风能利用系数为0.4;额定功率为4 kW;极对数为2;定子电阻为0.435 Ω;转子电阻为0.816 Ω;定子等效自感为71.31 mH;转子等效自感为71.31 mH;定转子等效互感为69.31 mH。

首先从该机组运行数据中选取了8个工况点(见表1)为研究工况，基本上均匀覆盖了正常转速范围。按照式(9)计算了各工况上的多输入多输出模型，进而对双馈发电机对象动态特性变化规律进行分析。例如在工况点2下，风电机组以0.18的转差率亚同步运行，按照式(9)计算出此时机组功率、转速等输出量对转速扰动、励磁电压变化等扰动量的传递函数阵Gp2(s)，如表2所示。

从表2列出的工况点2的线性模型数据来看，此对象具有三个极点，一个位于负实轴上(-189)，另外是一对负实部共轭复极点(-112±212i)，能够说明在此工况点上对象具有一定的稳定裕量。为了体现双馈发电机在整个变速运行范围中的动态特性变化规律，需要将8个工况点所对应的线性模型的极点分布变化情况进行综合比较。图4绘出了表1所列出的各工况点上的极点分布情况。

表1 双馈发电机运行工况点

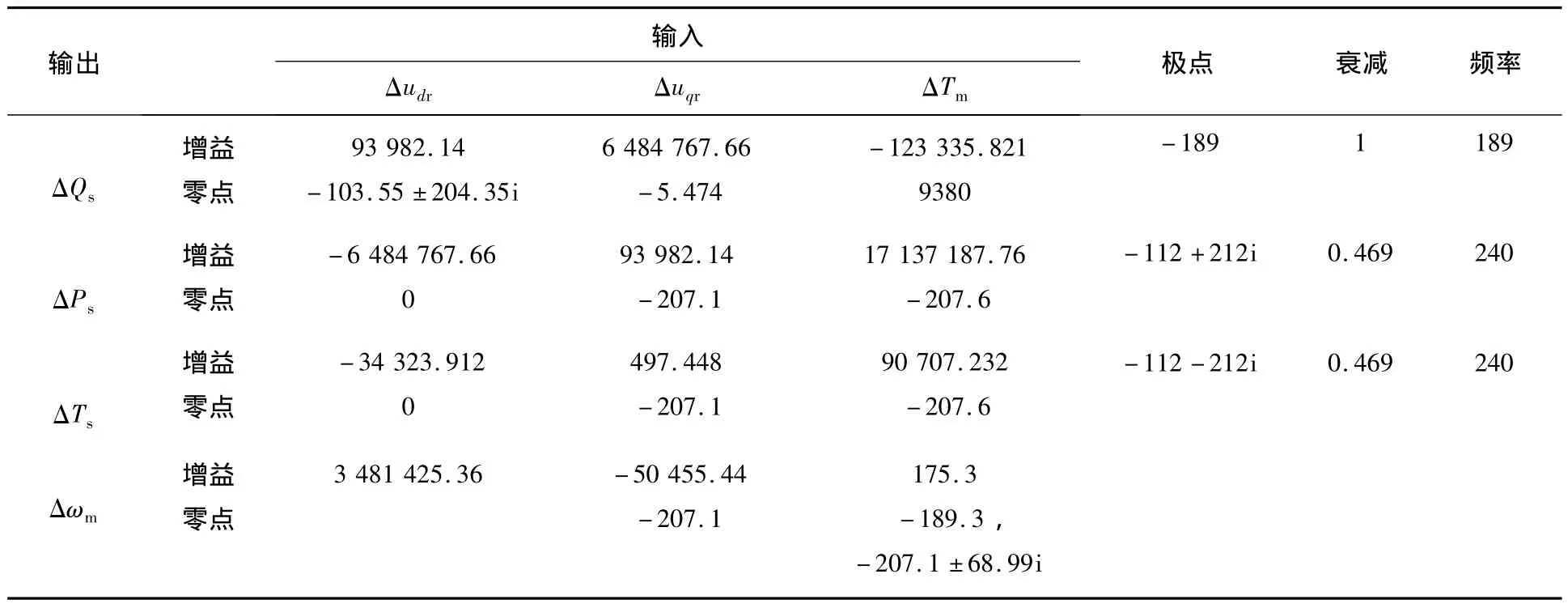
表2 工况点2上对象传递函数阵

从图4可知，1～8工况点上，双馈发电机对象的极点都是由一个实轴极点和一对共轭复极点组成，且全部分布在左半平面上。在发电机转速由亚同步向同步变化和由超同步向同步变化的过程中，极点变化移动的趋势相同，即对象动态特性与转差率正负无关。如工况1(转差率0.3)和工况8(转差率-2.8)时，系统极点分布基本相似。在转速向同步速靠近时，实轴极点快速远离虚轴，阻尼作用减弱;共轭复极点向虚轴运动，衰减系数略降;综合来看实轴极点的变化对对象作用影响更为主要，即同步速附近运行时发电机对象动态性能较好，而以大转差率运行时，对象阻尼较大，惯性时间较长。这就要求在整定PI控制器参数时要结合当前工作转速，再适当调整参数强弱以兼顾各工况时的控制效果，或在PI控制器前加分段折线函数来保证全程的稳定运行。

图4 各工况点上双馈发电机对象极点分布图

4 结语

为了研究双馈发电机变速恒频运行中动态特性变化情况，应用小扰动分析方法，建立了双馈发电机的线性模型。通过对某机组正常转速范围内典型工况点上的线性模型的极点分布情况分析表明:在正常转速范围内，对象都具有一定的稳定裕量，在发电机转速由亚同步或超同步向同步速变化的过程中，动态特性变化趋势一致，与转差率正负无关。且在同步速附近运行时有更好的动态特性，而以大转差率运行时，对象阻尼较大，惯性时间较长。分析结果为发电机控制系统设计及控制器参数整定提供了参考依据，具有实用价值。

［1］R Pena，J C CIare，G M Asher.Doubly fed induction generator using back-to-back PWM converters and its application to variable-speed wind-energy generation［J］.IEE Proc-Electr Power Appl，1996，143(3):231-241.

［2］汴松江，吕晓美，相会杰.交流励磁变速恒频风力发电系统控制策略的仿真研究［J］.中国电机工程学报，2005，25(16):57-62.

［3］刘其辉，贺益康，张建华.交流励磁变速恒频风力发电机的运行控制及建模仿真［J］.中国电机工程学报，2006(5):43-50.