基于DSP的永磁直线同步电动机无传感器功率角测量*

王福忠， 袁世鹰， 刘 静

(1.河南理工大学电气工程与自动化学院，河南焦作 454000;

2.中国矿业大学机电与信息工程学院，北京 100083)

0 引言

分段式永磁直线同步电动机(Permanent Magnet Linear Synchronous Motor，PMLSM)采用永磁体(动子)移动、电枢绕组(定子)分段的结构，适应于长距离、大推力的工业场合。但是，该电动机在运行中失步和机械振荡等问题一直困扰着电机的设计者和使用者。要实现该电机的稳定控制，抑制电机推力的波动都需要已知电机的动子位置与功率角。传统测量方法大多采用机械传感器法和反电动势法。机械传感器法需要在动子上安装相应的信号传感器，投资大。反电动势法是基于基波激励的方法，简单经济可靠，但在零速或低速时会因反电动势过小无法检测而失败。

为了能够获得包括零速的全速范围内电机动子位置及功率角，设计了基于DSP的高频电压注入法的分段式PMLSM功率角测量装置。

1 PMLSM功率角测量的基本原理

如果以PMLSM的定子a相绕组轴线为参考轴，功率角应等于动子永磁体在a相定子绕组中产生的感应电势V·a与a相绕组外加工作电压U·a之间的相位差角。由电机学原理可得，动子永磁体在a相定子绕组中产生的感应电势、a相定子绕组的供电电压、a相轴之间的关系如图1所示。图1中，θr为动子的位置角。

由图1可得PMLSM的功率角θ与动子位置角θr的关系为

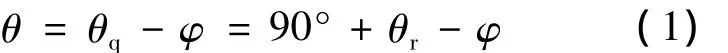
式中:φ——a相电压相对于定子a相绕组轴线的相位角，以ω做旋转运动。

式中:φ0为初始相位，可由电机刚起动时(t=0+)，施加在定子a相绕组上的电压和电流求得。利用式(2)计算φ时，时间为电压在每个周期内的旋转时间，即电压波形以a相绕组轴线为参考轴，每经过一个周期(对应的角度旋转360°)时间清零，重新开始计时。θr为动子位置角，是直线电机的d轴(旋转轴)在二个极距τ距离内与定子a相绕组轴线(非移动)之间的夹角，电机d轴每移动2个极距τ(对应的夹角移动360°)，θr重新开始计算。

由式(1)可知，求取PMLSM的功率角，首先需要得到动子的位置角θr。本文采用在PMLSM a相绕组中持续注入高频电压信号［1-7］，利用高阶带通滤波器提取高频电压与电流信号，进而计算出电机动子位置角θr。

图1 直线电机功率角与动子位置角关系图

1.1 电机凸极效应和动子位置角及高频电流三者关系式

为了简化分析，假设:铁心非饱和，电机中的涡流损耗和磁滞损耗、电机绕组漏感可以忽略，气隙中的磁势呈正弦分布。

在以上假设情况下，利用电机分析理论，建立高频激励下的 PMLSM的数学模型为:假设在PMLSM的a相绕组上注入高频电压的角频率为ωi，幅值为Ui，则该高频电压信号可表示为

经A-B-C坐标系向α-β坐标系变换，得到在α-β坐标系下高频电压信号为

式(3)中，由于注入的高频电压信号频率远高于基波频率，定子电阻的影响可以忽略，故在α-β坐标系下，PMLSM的电压数学模型也可以用式(4)表示:

式中:Lαβ——α-β 坐标系下的电感矩阵;

iαβ——α-β 坐标系下的高频电流。

α-β坐标系下的电感矩阵为［3］

由式(5)可看出电感矩阵Lαβ中包含动子位置角信息，其中:L为平均电感，L=(Ld+Lq)/2;ΔL为半差电感，ΔL=(Lq-Ld)/2;θr为动子位置角;Ld为直轴电感;Lq为交轴电感。

根据式(2)、(4)、(5)可求得高频激励下PMLSM的电流:

折算到A-B-C坐标系，a相电流为

由式(7)可得a相高频电流信号的幅值Ia:

由式(9)可以看出，由于PMLSM的d轴和q轴电感不相等(即ΔL≠0)，则a相高频电流信号的幅值Ia与动子位置角信息有关。在ΔL、L已知的情况下，利用式(9)可求得凸极式PMLSM的动子位置角θr。

1.2 高频电流信号幅值的获取方法

本文采用半周积分算法求得高频电流幅值，其公式为

可得a相高频电流信号的幅值Ia中包含有动子位置角信息，将式(8)变形可得PMLSM的动子位置角θr:

式中:Ts——采样间隔;

ik——第k次采样值;

N——一个周期内的采样点数，为了提高计算精度，选取N=48，即采样频率为48 kHz;

i0——k=0 时的采样值;

iN/2——k=N/2 时的采样值。

应用式(10)可求得电流幅值Ia。

2 测量系统硬件设计

功率角测量装置主要任务是完成电机A相绕组的工作电压获取、高频激励信号的产生、高频电压与各段电枢A绕组的高频电流信号的检测及功率角的计算，其硬件组成如图2所示。数字信号处理器(DSP)选择具有3.3 V的外围接口电压、低功耗的TMS320F2812处理器。外部扩展了1M字存储器、液晶显示器、A/D转换器、通信电路、键盘电路等。工作原理为:电压和电流传感器获取高频电压、各段定子的高频电流信号，经1 kHz带通滤波器，送入ADS8364;而电机a相绕组的工作电压则由电压传感器获取后，经低通滤波器，送入ADS8364;然后DSP中央处理单元将利用式(10)和式(9)计算出电机的动子位置角，再利用式(1)和式(2)计算出电机的功率角，并通过通信接口送往监控PC。

图2 功率角测量系统基本结构框图

2.1 高频信号发生器的设计［8］

高频信号利用TMS320F2812输出的正弦脉宽调制(SPWM)波产生，其原理如图3所示。图中缓冲电路的作用是对PWM口输出的SPWM波进行缓冲，并将电压拉高到约12 V，以供后级低通滤波电路使用。这一部分电路由两个芯片组成:一片用三态缓冲器，由于PWM口的输出为3.3 V TTL电平，为了保证与后级接口芯片的电平一致，则选用74HCT04芯片实现TTL与COMS电路之间的电平转换;另一片选用光电藕合器6N137实现电路之间的隔离。滤波电路的主要作用是将直流脉动信号转换成正弦交流信号，采用简单的R-C电路。

图3 高频信号发生器的原理结构框图

减法电路的主要作用是将0～20 V正弦交流信号转换成-10 V～+10 V正弦交流信号，设计时可利用差分式电路来实现其功能。为了简化电路，选用美国AD公司的精密仪表放大器AD524作为前置放大。AD524采用双电源供电，供电电压为±15 V。为了提高驱动能力，输出电路采用对管TIP35C和TIP36C作为功率晶体管。

2.2 耦合电容器和电压电流互感器选型

(1)耦合电容器的选择。耦合电容器的作用主要是实现高频信号发生器与电机的工作电源之间的隔离。要求在1 kHz的高频电压信号下其阻抗尽量小，而在电机的电源工作频率下其阻抗越大越好，并满足耐压要求。由于试验电机的电源工作频率为15 Hz以下，电压在200 V以下，因此，选择的耦合电容器的参数为:C=10 μF(x=100);耐压电压为800 V。

(2)电压和电流互感器的选择。为了能够快速、精确地测量高频电压与电流信号及a相绕组的工作电压，选用线性度好，灵敏度高的霍尔型电压和电流传感器。其中霍尔型电压传感器的参数为:电压检测范围为～300 V;精度为0.5/1 000。霍尔型电流传感器的参数为:电流检测范围为～0.5 A;精度为0.5/1 000;电压和电流互感器的输出均为4～20 mA。

2.3 1 kHz带通滤波器设计

测量的高频电压和电流信号中含有低次谐波信号、PWM开关谐波电流及其他干扰信号。为了把微弱的、频率为1kHz的高频电压和电流信号从强噪声背景中检测出来，选择了美国MAXIM公司开发的8阶连续时间有源滤波器芯片MAX274，将4个二阶结合，构成了如图4所示的8阶切比雪夫带通滤波器。

图4 滤波器接线图

2.4 A/D转换模块的选择及其与DSP的接线

A/D转换器件的性能决定着系统性能的优劣。为了保证测量精度、电压与电流采样同时性及48 kHz采样频率的要求，功率角测量装置选用TI公司的ADS8364作为A/D转换模块。该器件具有高速(采样频率250 kHz)、低功耗、6通道同步采样与转换、单+5 V供电、16位高速并行接口等特点，完全满足本系统的要求。

由于ADS8364和TMS320F2812都是TI公司生产的高速芯片，故两者在速度上能够完全匹配，可以实现芯片间的无缝连接。本系统选择直接地址读方式，由XA［2∶0］作为变换结果寄存器低位地址，当ADS8364的CS引脚为高电平时，其数据总线处于高阻状态，当CS引脚置低电平时，并口数据总线上输出当前数据。具体的连接如图5所示。为了实现6个通道的同步采样，把TMS320F2812的GPIDB15引脚与ADS8364的HOLDA、HOLDB、HOLDC信号相连，控制6个采样/保持器的同步。

图5 ADS8364与和TMS320F2812的连接图

2.5 高频电压信号注入方式与信号获取接线

由于用于驱动提升系统的PMLSM，运行距离长，定子电枢绕组分的段数较多，制造与安装时不可能做到各段电枢绕组与动子永磁体之间的气隙完全均匀相等和各段电感量一致。为了减少气隙不均匀的影响，在测量时，测量装置应时刻跟踪电机动子永磁体的运动位置，得到与动子永磁体相耦合的定子电枢绕组，选取对应的电感值，来消除由于电机气隙变化所导致的误差。高频电压信号注入方式与信号获取接线原理如图6所示。

3 功率角测试试验

试验电机是4段式PMLSM，4载荷1.2 t。电机各段初级电枢绕组的参数为:单台定子长度680 mm，槽数39，极数2p=12，极距 τ=51 mm，电枢绕组的电抗Xt=9.83 Ω;电阻R=2.985 Ω，额定电流Iamax=25 A。

利用图2所示的功率角测量系统，并按照图6所示的功率角测量原理进行了接线和试验。为了验证测量精度，用一个直线光栅尺同时进行功率角测量，将DSP测量系统测得的功率角与直线光栅尺测得的功率角进行比较，验证DSP测量系统的测量精度。

图6 高频信号注入与获取接线原理图

表1为分别采用光栅尺和高频注入法获得的PMLSM的动子位置角。由该表可看出最大静态误差为 ±1°。将表1所示的数据代入式(1)、(2)，分别计算出的PMLSM功率角的误差小于±1.6°，满足控制所需要的精度。说明建立PMLSM功率角测量数学解析模型合理，设计的DSP测量系统精度满足要求。

4 结语

建立了PMLSM的功率角与动子位置角的关系方程和高频激励下的该电机的高频电流电枢电感-动子位置角之间的解析方程，设计了基于DSP的高频信号注入法PMLSM动子功率角检测系统。实践表明:

(1)采用高频信号注入法求取动子的PMLSM动子位置角和功率角，实时性好，精度满足要求;

(2)TMS320F2812具有高速的工作频率，丰富的片上外设，充分满足了PMLSM动子位置角和功率角测量的需要;

表1 动子位置角测试结果对照表

(3)A/D转换模块的选择以及设计其接口电路时，应保证测量精度、电压与电流的采样同时性及采样频率的要求。

［1］余佩琼，陆亿红，王涌.永磁直线同步电动机无位置传感器控制系统的研究［J］.中国电机工程学报，2007，27(24):53-57.

［2］陆华才，徐月同，余佩琼，等.永磁直线电机绕组电感饱和效应的有限元分析及应用［J］.中国电机工程学报，2006，26(25):109-113.

［3］秦峰，贺益康.两种高频注入法的无传感器运行研究［J］.中国电机工程学报，2005，25(5):116-121.

［4］Jang J H，Sul S K，Ha J 1.Sensorless drive of surfacemounted permanent-magnet motor by high-frequency signal injection based on magnetic saliency［J］.IEEE Trans on industry Applications，2003，39(4):1031-1038.

［5］Jang J H，Ha J I.Analysis of permanent-magnet machine for sensorless control based on high-frequency signal injection［J］.IEEE Tarns on Industry Appilcaitons，2004，40(6):1595-1604.

［6］王福忠，汪旭东，焦留成，等.同步电动机电磁力角与最大推力控制策略的研究［J］.煤炭学报，2001，26(3):307-312.

［7］王福忠，焦留成，袁世鹰.基于神经网络永磁直线同步电动机提升系统动态模型建立与仿真［J］.系统仿真学报，2002，24(9):1249-1254.

［8］宋萌.基于DSP的正弦信号发生器设计［J］.电子元器件应用，2006(9):64-66.